Bài 2.5 trang 28 Toán lớp 7: Làm tròn số 3,14159…

a) đến chữ số thập phân thứ ba;

b) với độ chính xác 0,005.

Phương pháp giải: 

Lời giải: 

Số 3,14159… làm tròn đến chữ số thập phân thứ ba là: 3,142 ( vì chữ số ngay sau chữ số hàng làm tròn là chữ số 5 $\ge$5 )

Số 3,14159… làm tròn với độ chính xác 0,005, tức là làm tròn số 3,14159... đến hàng phần trăm, ta được kết quả là 3,14 ( vì chữ số chữ số hàng làm tròn là chữ số 1 < 5)

Lý thuyết Làm quen với số thập phân vô hạn tuần hoàn

1. Số thập phân vô hạn tuần hoàn

• Số thập phân vô hạn tuần hoàn là biểu diễn thập phân của một số có phần thập phân lặp lại (lặp lại giá trị của nó ở các khoảng đều đặn) và phần lặp lại vô hạn không phải là số không.

• Chu kì của số thập phân vô hạn tuần hoàn là phần được lặp lại vô hạn lần.

• Số thập phân hữu hạn là số thập phân như 0,34; 1,2; 6,7; …

Ví dụ:

+ Khi chia 7 cho 3 được thương là 2,333…, chữ số 3 được lặp lại mãi. Nên $\frac{7}{3}=2,333...=2,\left(3\right)$ là số thập phân vô hạn tuần hoàn với chu kì là 3.

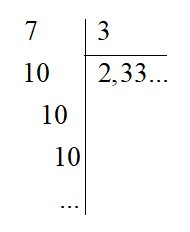
+ Phân số $\frac{19}{11}=1,\mathrm{727272...}=1,\left(72\right)$ là số thập phân vô hạn tuần hoàn với chu kì là 72.

+ Phân số $-\frac{1009}{900}=-1,\mathrm{12111...}=-1,21\left(1\right)$ là số thập phân vô hạn tuần hoàn với chu kì là 1.

Chú ý:

• Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ví dụ:  Số $\frac{12}{5}=2,4$;  $-\frac{1}{15}=-0,\mathrm{0666...}=-0,0\left(6\right).$

2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước

Khi làm tròn số đến một hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.

Ví dụ:

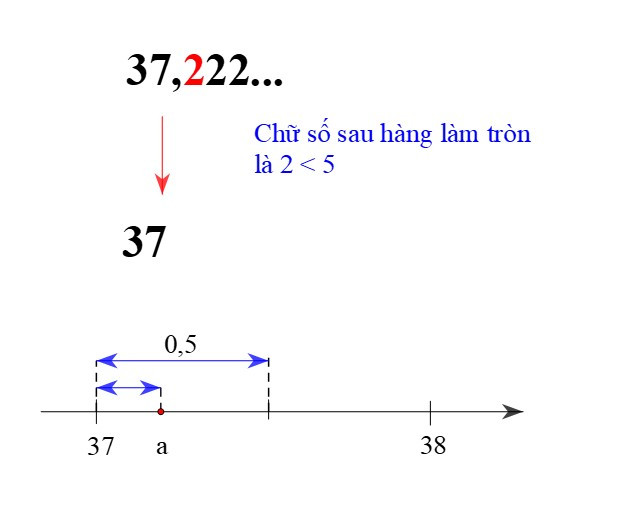
+ Làm tròn a = 37,222… đến hàng đơn vị thì được kết quả là 37. Ta viết 37,222… ≈ 37. Ta cũng nói rằng 37 là kết quả làm tròn của a = 37,222… với độ chính xác là 0,5.

+ Làm tròn số 17,213… đến hàng phần mười ta được kết quả 17,213… ≈ 17,2 với độ chính xác là 0,05.

+ Để làm tròn số 129,18 với độ chính xác là 5, ta làm tròn đến hàng chục. Ta được 129,18 ≈ 130.

Chú ý:

• Muốn làm tròn số thập phân với độ chính xác cho trước, ta có thể xác định hàng làm tròn thích hợp bằng cách sử dụng bảng dưới đây.

Đọc thêm

• Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó được viết dưới dạng số thập phân hữu hạn. Ví dụ:

$\frac{3}{10}=\frac{3}{2.5}=0,3$

• Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó được viết dưới dạng số thập phân vô hạn tuần hoàn. Ví dụ:

$\frac{1}{14}=\frac{1}{2.7}=0,\mathrm{0714285714285...}$

• Mỗi số thập phân vô hạn tuần hoàn biểu diễn một số hữu tỉ. Ví dụ:

$0,\left(1\right)=\frac{1}{9}$; $0,\left(01\right)=\frac{1}{99}$; $0,\left(21\right)=\frac{21}{99}$; $0,\left(9\right)=1$.

Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 1

Bài 6: Số vô tỉ. Căn bậc hai số học

Bài 7: Tập hợp các số thực

Luyện tập chung trang 37