Với giải sách bài tập Toán 8 Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Giải SBT Toán 8 trang 43

Bài 1 trang 43 SBT Toán 8 Tập 1: Tính diện tích xung quanh của hình chóp tam giác đều có cạnh đáy 10 cm và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều bằng 15 cm.

Lời giải:

Diện tích xung quanh của hình chóp tam giác đều là:

$S_{xq}=3.\frac{10.15}{2}=225$ (cm²).

Bài 2 trang 43 SBT Toán 8 Tập 1: Tính diện tích toàn phần của hình chóp tứ giác đều có cạnh đáy 30 m và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 35 m.

Lời giải:

Diện tích toàn phần của hình chóp tứ giác đều là:

$S_{tp}=S_{đáy}+S_{xq}={30}^2+4.\frac{30.35}{2}=3000$ (cm²).

Bài 3 trang 43 SBT Toán 8 Tập 1: Tính thể tích của hình chóp tam giác đều có chiều cao 34 cm và tam giác đáy có cạnh 16 cm, chiều cao $8\sqrt{3}$cm (Làm tròn kết quả đến hàng phần mười.)

Lời giải:

Thể tích của hình chóp tam giác đều là:

$V=\frac{1}{3}.S_{đáy}.h=\frac{1}{3}.\frac{16.8\sqrt{3}}{2}.34\approx 1256,3$ (cm³).

Bài 4 trang 43 SBT Toán 8 Tập 1: Tính thể tích của hình chóp tứ giác đều có chiều cao 24 cm, tứ giác đáy có cạnh 15 cm.

Lời giải:

Thể tích của hình chóp tứ giác đều là:

$V=\frac{1}{3}.S_{đáy}.h=\frac{1}{3}.{15}^2.24=1800$ (cm³).

Bài 5 trang 43 SBT Toán 8 Tập 1: Một chiếc gàu có dạng hình chóp tam giác đều và một chiếc bình có dạng hình lăng trụ đứng tam giác có cùng diện tích đáy. Người ta đổ 6 gàu nước vào bình và đo được mực nước trong bình tăng thêm 1,2 m. Tính chiều cao của chiếc gàu.

Lời giải:

Gọi diện tích đáy của chiếc gàu (cũng là diện tích đáy của bình) là S, thể tích của chiếc gàu là V, chiều cao của chiếc gàu là h, ta có$V=\frac{1}{3}.S.h$

Khi đổ 6 gàu nước vào bình thì thể tích 6 gàu nước là:

$6V=6.\frac{1}{3}.S.h=2Sh$.

Thể tích của nước được đổ vào trong bình là: S.1,2 (m³).

Do mực nước trong bình tăng lên 1,2 m sau khi đổ thêm 6 gàu nước nên 2Sh = S.1,2

Suy ra h = 0,6 m.

Giải SBT Toán 8 trang 44

Bài 6 trang 44 SBT Toán 8 Tập 1: Một khối gỗ gồm một hình chóp tứ giác đều và một hình lập phương có chung đáy (Hình 3). Tính thể tích của khối gỗ, biết chiều cao của hình chóp tứ giác đều là 50 cm và cạnh của hình lập phương là 40 cm. (Làm tròn kết quả đến hàng phần mười.)

Lời giải:

Gọi thể tích của khối lập phương là V₁, thể tích của hình chóp tứ giác đều là V₂, thể tích khối gỗ là V.

Khi đó ta có:

• Thể tích hình lập phương là: $V_1={40}^3=64000$ (cm³).

• Thể tích của hình chóp tứ giác đều: $V_2=\frac{1}{3}.{40}^2.50\approx 26666,7$ (cm³).

• Thể tích của khối gỗ là: V = V₁ + V₂ ≈ 64 000 + 26 666,7 = 90 666,7 (cm³).

Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hình chóp tam giác đều - Hình chóp tứ giác đều

Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Bài tập cuối chương 2

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Lý thuyết Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Công thức tính diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều

Diện tích xung quanh của hình chóp tam giác đều (hình chóp tứ giác đều) bằng tổng diện tích của các mặt bên.

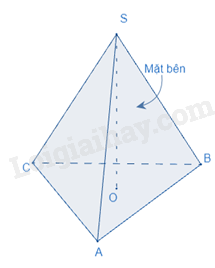
Diện tích toàn phần của hình chóp tam giác đều (hình chóp tứ giác đều) bằng tổng của diện tích xung quanh và diện tích đáy:  ($S_{tp}=S_{xq}+S_{đáy}$ ($S_{tp}$ là diện tích toàn phần,  là diện tích đáy, $S_{xq}$ là diện tích xung quanh)

Công thức tính thể tích của hình chóp tam giác đều và hình chóp tứ giác đều

Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng $\frac{1}{3}$ diện tích đáy nhân với chiều cao.

$V=\frac{1}{3}{S}_{đáy}.h$. 

(V là thể tích, $S_{đáy}$ là diện tích đáy, $h$ là chiều cao)

Ví dụ:

Cho hình chóp tứ giác đều sau:

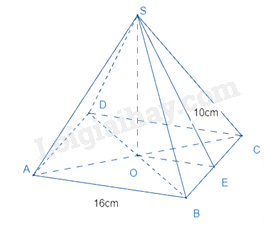
Diện tích xung quanh của hình chóp là: $S_{xq}=4.\frac{1}{2}.10.16=320(c{m}^2)$

Diện tích toàn phần của hình chóp là: $$S_{tp}=S_{xq}+S_{đáy}=320+16.16=576(c{m}^2)$$

Chiều cao của hình chóp là: $\sqrt{{10}^2-{\left(\frac{16}{2}\right)}^2}=\sqrt{100-64}=\sqrt{36}=6(cm)$

Thể tích của hình chóp là: $V=\frac{1}{3}.6.16.16=512(c{m}^3)$