Bài 1.2 trang 7 SBT Toán 11 Tập 1: Trên đường tròn lượng giác, xác định điểm Q biểu diễn các góc lượng giác có số đo sau:

a) $\frac{\pi }{6}$ ;                     b) $\frac{-5\pi }{7}$ ;

c) 270°;                         d) – 415°.

Lời giải:

a) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là $\frac{\pi }{6}$  được xác định như hình dưới đây.

b) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là $\frac{-5\pi }{7}$  được xác định như hình dưới đây.

c) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là 270° được xác định như hình dưới đây.

d) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là – 415° được xác định như hình dưới đây.

Bài 1.3 trang 7 SBT Toán 11 Tập 1: Một đường tròn có bán kính 20 m. Tìm độ dài của cung trên đường tròn đó có số đo là:

a) $\frac{2\pi }{7}$ ;                  b) 36°. 

Lời giải:

a) Ta có l = Rα = 20 . $\frac{2\pi }{7}=\frac{40\pi }{7}$  (m).

b) Ta có l = R . $\frac{\pi a}{180}=20.\frac{\pi .36}{180}=4\pi$  (m).

Bài 1.4 trang 7 SBT Toán 11 Tập 1: Cho cos x = $-\frac{5}{13}$  (90° < x < 180°). Tính các giá trị lượng giác còn lại của góc x.

Lời giải:

Từ đẳng thức sin² x + cos² x = 1, suy ra

sin² x = 1 – cos² x = $1-{\left(-\frac{5}{13}\right)}^2=\frac{144}{169}$

Mặt khác 90° < x < 180° nên sinx > 0. Do đó sin x = $\sqrt{\frac{144}{169}}=\frac{12}{13}$ .

Suy ra tan x = $\frac{\sin x}{\cos x}=\frac{12}{13}:\left(-\frac{5}{13}\right)=-\frac{12}{5}$ , cot x = $\frac{\cos x}{\sin x}=\left(-\frac{5}{13}\right):\frac{12}{13}=-\frac{5}{12}$ .

Bài 1.5 trang 7 SBT Toán 11 Tập 1: Cho sin a + cos a = m. Hãy tính theo m.

a) sin a cos a;

b) sin³ a + cos³ a;

c) sin⁴ a + cos⁴ a.

Lời giải:

a) Ta có: sin a + cos a = m nên (sin a + cos a)² = m²

hay sin² a + cos² a + 2sin a cos a = m² hay 1 + 2sin a cos a = m².

Từ đó suy ra sin a cos a = $\frac{m^2-1}{2}$ .

b) sin³ a + cos³ a = (sin a + cos a)³ – 3sin a cos a(sin a + cos a)

= m³ – 3m $\frac{m^2-1}{2}=\frac{3m-m^3}{2}$.  

c) sin⁴ a + cos⁴ a = (sin² a + cos² a)² – 2sin² a cos² a

= 1 – 2(sin a cos a)² = $1-2.{\left(\frac{m^2-1}{2}\right)}^2=1-\frac{{\left(m^2-1\right)}^2}{2}$ .

Bài 1.6 trang 7 SBT Toán 11 Tập 1: Chứng minh các đẳng thức sau:

a) cos⁴ x – sin⁴ x = 2 cos² x – 1;

b) tan² x – sin² x = tan² x . sin² x;

c) (sin x + cos x)² + (sin x – cos x)² = 2.     

Lời giải:

a) Ta có VT = cos⁴ x – sin⁴ x

= (cos² x – sin² x)(cos² x + sin² x)

= cos² x – sin² x

= cos² x – (1 – cos² x) = 2 cos² x – 1 = VP.                   

b) Ta có

VT = tan² x – sin² x = $\frac{{\sin }^{2}x}{{\cos }^{2}x}-{\sin }^{2}x$$=\frac{{\sin }^{2}x-{\sin }^{2}x{\cos }^{2}x}{{\cos }^{2}x}$$=\frac{{\sin }^{2}x\left(1-{\cos }^{2}x\right)}{{\cos }^{2}x}$

$=\frac{{\sin }^{2}x}{{\cos }^{2}x}.{\sin }^{2}x$ = tan² x . sin² x = VP.                    

c) Ta có

VT = (sin x + cos x)² + (sin x – cos x)²

= sin² x + 2sin x cos x + cos² x + sin² x – 2sin x cos x + cos² x

= 2 sin² x + 2 cos² x = 2(sin² x + cos² x) = 2 . 1 = 2 = VP.

Giải SBT Toán 11 trang 9 Tập 1

Bài 1.7 trang 9 SBT Toán 11 Tập 1: Rút gọn biểu thức

A = 2cos⁴ x – sin⁴ x + sin² x cos² x + 3 sin² x.

Lời giải:

A = 2cos⁴ x – sin⁴ x + sin² x cos² x + 3 sin² x

= cos⁴ x – sin⁴ x + cos⁴ x + sin² x cos² x + 3 sin² x

= (cos² x – sin² x)(cos² x + sin² x) + cos² x (cos² x + sin² x) + 3sin² x

= cos² x – sin² x + cos² x + 3 sin² x

= 2cos² x + 2 sin² x

= 2(cos² x + sin² x)

= 2 . 1 = 2.

Bài 1.8 trang 9 SBT Toán 11 Tập 1: Bánh xe của người đi xe đạp quay được 12 vòng trong 6 giây.

a) Tính góc (theo độ và rađian) mà bánh xe quay được trong 1 giây.

b) Tính quãng đường mà người đi xe đạp đã đi được trong 1 phút, biết rằng đường kính bánh xe đạp là 860 mm.

Lời giải:

a) Trong 1 giây, bánh xe quay được $\frac{12}{6}$  = 2 vòng, tức là quay được một góc 4π (rad) hay 720°.

b) Bán kính xe đạp là: 860 : 2 = 430 (mm).

Trong 1 phút, quãng đường mà người đi xe đã đi được là:

l = 430 . 4π . 60 = 103 200π (mm).

Bài 1.9 trang 9 SBT Toán 11 Tập 1: Kim giờ dài 6 cm và kim phút dài 11 cm của đồng hồ chỉ 4 giờ. Hỏi thời gian ít nhất để 2 kim vuông góc với nhau là bao nhiêu? Lúc đó tổng quãng đường hai đầu mút kim giờ và kim phút đi được là bao nhiêu?

Lời giải:

Một giờ, kim phút quét được một góc lượng giác 2π; kim giờ quét được một góc $\frac{\pi }{6}$ .

Hiệu vận tốc giữa kim phút và kim giờ là $2\pi -\frac{\pi }{6}=\frac{11\pi }{6}$ .

Vào lúc 4 giờ hai kim tạo với nhau một góc là $\frac{2\pi }{3}$ .

Khoảng thời gian ít nhất để hai kim vuông góc với nhau là

$\left(\frac{2\pi }{3}-\frac{\pi }{2}\right):\frac{11\pi }{6}=\frac{1}{11}$ (giờ).

Vậy sau $\frac{1}{11}$  (giờ) hai kim sẽ vuông góc với nhau.

Tổng quãng đường hai đầu mút kim đi được là

l = R .α = $6.\frac{1}{11}.\frac{\pi }{6}+11.\frac{1}{11}.2\pi =\frac{23\pi }{11}$  (cm).

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 1: Giá trị lượng giác của góc lượng giác

Bài 2: Công thức lượng giác

Bài 3: Hàm số lượng giác

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Lý thuyết Giá trị lượng giác của góc lượng giác

1. Góc lượng giác

a, Khái niệm góc lượng giác và số đo của góc lượng giác

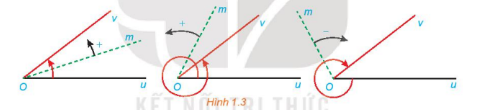
Trong mặt phẳng, cho 2 tia Ou, Ov. Xét tia Om cùng nằm tròn mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou và tia cuối Ov.

Kí hiệu: (Ou, Ov).

Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov kí hiệu là sđ(Ou, Ov).

b, Hệ thức Chasles

Với 3 tia Ou, Ov, Ow bất kì ta có:

Sđ(Ou,Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) +k360^o.

2. Đơn vị đo góc và độ dài cung tròn

a, Đơn vị đo góc và cung tròn

Đơn vị độ: $1^o={60}^{\prime },1^{\prime }={60}^{″}$

Đơn vị rađian: $1^o=\frac{\pi }{180}$rad, 1 rad =${\left(\frac{180}{\pi }\right)}^o$

b, Độ dài cung tròn

Một cung tròn của đường tròn bán kính R và có số đo $\alpha$rad thì có độ dài $l=R\alpha$

3. Giá trị lượng giác của góc lượng giác

a, Đường tròn lượng giác

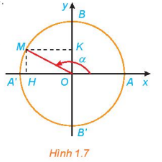
Đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1, được định hướng và lấy điểm A(1;0) làm điểm gốc của đường tròn.

Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo $\alpha$(độ hoặc rad) là điểm M trên đường tròn lượng giác sao cho sđ (OA, OM) =$\alpha$.

b, Các giá trị lượng giác của góc lượng giác:

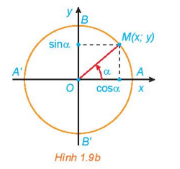
Trục tung là trục sin, trục hoành là trục côsin

Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:

$x=$cos$\alpha$, $y=$sin$\alpha$.

tan$\alpha$$=\frac{\sin \alpha }{\cos \alpha }=\frac{y}{x}\left(x\ne 0\right)$

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{x}{y}\left(y\ne 0\right)$.

c, Bảng xác định dấu của các giá trị lượng giác

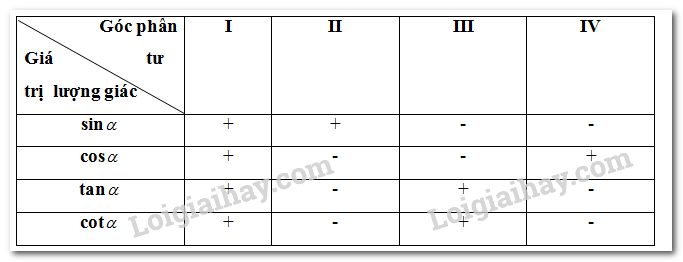
d, Giá trị lượng giác của các góc đặc biệt

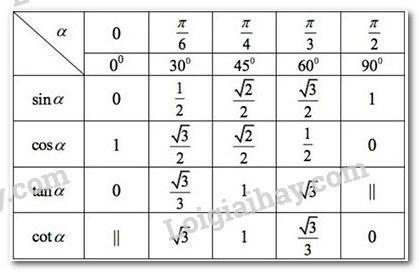
e, Cách bấm máy tính để tìm giá trị lượng giác của góc

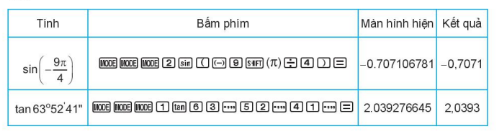
4. Quan hệ giữa các giá trị lượng giác

a, Các công thức lượng giác cơ bản

$\begin{array}{l}{\sin }^2\alpha +{\cos }^2\alpha =1\\ 1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }\left(\alpha \ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right)\\ 1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }\left(\alpha \ne k\pi ,k\in \mathbb{Z}\right)\\ \tan \alpha .\cot \alpha =1\left(\alpha \ne \frac{k\pi }{2},k\in \mathbb{Z}\right)\end{array}$

b, Giá trị lượng giác của các góc có liên quan đặc biệt (cos đối, sin bù, phụ chéo, khác pi tan)

• Góc đối nhau ($\alpha$ và - $\alpha$)

$\begin{array}{l}\sin \left(-\alpha \right)=-\sin \alpha \\ \cos \left(-\alpha \right)=\cos \alpha \\ \tan \left(-\alpha \right)=-\tan \alpha \\ \cot \left(-\alpha \right)=-\cot \alpha \end{array}$

• Góc bù nhau ($\alpha$ và $\pi$ - $\alpha$)

$\begin{array}{l}\sin \left(\pi -\alpha \right)=\sin \alpha \\ \cos \left(\pi -\alpha \right)=-\cos \alpha \\ \tan \left(\pi -\alpha \right)=-\tan \alpha \\ \cot \left(\pi -\alpha \right)=-\cot \alpha \end{array}$

• Góc phụ nhau ($\alpha$ và $\frac{\pi }{2}$ - $\alpha$)

$\begin{array}{l}\sin \left(\frac{\pi }{2}-\alpha \right)=c\mathrm{o}\mathrm{s}\alpha \\ \cos \left(\frac{\pi }{2}-\alpha \right)=\sin \alpha \\ \tan \left(\frac{\pi }{2}-\alpha \right)=\cot \alpha \\ \cot \left(\frac{\pi }{2}-\alpha \right)=\tan \alpha \end{array}$

• Góc hơn kém $\pi$ ($\alpha$ và $\pi$ + $\alpha$)

$\begin{array}{l}\sin \left(\pi +\alpha \right)=-\sin \alpha \\ \cos \left(\pi +\alpha \right)=-\cos \alpha \\ \tan \left(\pi +\alpha \right)=\tan \alpha \\ \cot \left(\pi +\alpha \right)=\cot \alpha \end{array}$