Với giải Bài 5 trang 80 VTH Toán lớp 8 Kết nối tri thức chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải VTH Toán 8 Bài tập cuối chương 4
Bài 5 trang 80 vở thực hành Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.
a) Chứng minh rằng AE = DF.
b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.
Lời giải:
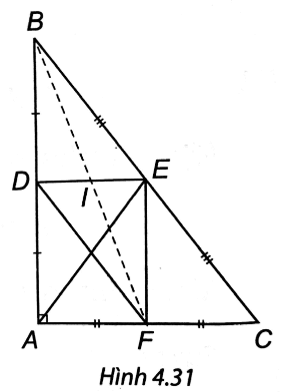
a) ∆ABC có: D là trung điểm AB, E là trung điểm BC, nên DE là đường trung bình của ∆ABC.
Suy ra DE // AC và DE = AC.
Xét tứ giác ADEF: DE // AF và DE = AF nên tứ giác ADEF là hình bình hành.
Ta lại có nên tứ giác ADEF là hình chữ nhật.
Suy ra AE = DF.
b) ∆ABC có: D là trung điểm AB, F là trung điểm AC nên DF là đường trung bình của ∆ABC.
Suy ra DF // BC và DF = BC = BE.
Xét tứ giác BDFE: DF // BE và DF = BE nên tứ giác BDFE là hình bình hành.
Suy ra hai đường chéo DE và BF cắt nhau tại trung điểm của mỗi đường.
Ta lại có I là trung điểm của DE nên I cũng là trung điểm của BF.
Vậy B, I, F thẳng hàng.
Xem thêm lời giải bài tập Vở thực hành Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải Vở thực hành Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 18: Thu thập và phân loại dữ liệu
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
