Giải SBT Toán 7 trang 62 Tập 1 Kết nối tri thức

Nguyễn Thị Thuỳ Linh Ngày: 26-07-2022 Lớp 7

3.5 K

Với lời giải SBT Toán 7 trang 62 Tập 1 chi tiết trong Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

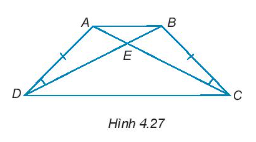
Bài 4.27 trang 62 SBT Toán 7 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC, $\hat{A D E} = \hat{B C E}$ . Chứng minh rằng:

a) $\hat{D A C} = \hat{C B D}$ .

b) ∆AED = ∆BEC.

c) AB song song với DC.

Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

a) Xét tam giác AED có:

$\hat{A D E} + \hat{D A E} + \hat{A E D} = 180 °$

$\hat{D A E} = 180 ° - \hat{A D E} - \hat{A E D}$ (1)

Xét tam giác BEC có:

$\hat{B C E} + \hat{E B C} + \hat{B E C} = 180 °$

$\hat{E B C} = 180 ° - \hat{B C E} - \hat{B E C}$ (2)

Mà $\hat{A D E} = \hat{B C E}$ ; $\hat{A E D} = \hat{B E C}$ (hai góc đối đỉnh) (3)

Từ (1); (2); (3) suy ra, $\hat{D A E} = \hat{E B C}$ hay $\hat{D A C} = \hat{C B D}$ (điều phải chứng minh).

b) Xét ∆AED và ∆BEC ta có:

$\hat{D A E} = \hat{E B C}$ (chứng minh trên)

$\hat{A D E} = \hat{B C E}$ (giả thiết)

AD = CB (giả thiết)

Do đó, ∆AED = ∆BEC (g – c – g).

c) Vì ∆AED = ∆BEC nên AE = BE; ED = EC.

Ta có: AC = AE + EC; BD = BE + ED.

Do đó, AC = BD.

Xét ∆ABD và ∆BAC ta có:

AC = BD (chứng minh trên)

AB chung

AD = CB (giả thiết)

Do đó, ∆ABD = ∆BAC (c – c – c)

Suy ra $\hat{A B D} = \hat{B A C}$ (hai góc tương ứng)

Xét tam giác AEB có:

$\hat{A B E} + \hat{B A E} + \hat{A E B} = 180 °$

Do đó, $2 \hat{A B E} = 180 ° - \hat{A E B}$ (vì $\hat{A B E} = \hat{B A E}$ do $\hat{A B D} = \hat{B A C}$ )

Suy ra $\hat{A B E} = \frac{180 ° - \hat{A E B}}{2}$ (4)

Xét ∆ACD và ∆BDC ta có:

AC = BD (chứng minh trên)

CD chung

AD = CB (giả thiết)

Do đó, ∆ACD = ∆BDC (c – c – c)

Suy ra $\hat{A C D} = \hat{B D C}$ (hai góc tương ứng)

Xét tam giác DEC có:

$\hat{D C E} + \hat{E D C} + \hat{D E C} = 180 °$

Do đó, $2 \hat{E D C} = 180 ° - \hat{D E C}$ (vì $\hat{E D C} = \hat{D C E}$ do $\hat{A C D} = \hat{B D C}$ )

Suy ra $\hat{E D C} = \frac{180 ° - \hat{D E C}}{2}$ (5)

Lại có, $\hat{A E B}, \hat{D E C}$ là hai góc đối đỉnh nên $\hat{A E B} = \hat{D E C}$ (6)

Từ (4); (5); (6) suy ra $\hat{A B E}$ = $\hat{E D C}$ hay $\hat{A B D} = \hat{B D C}$ .

Mà hai góc này lại ở vị trí so le trong nên AB // CD.

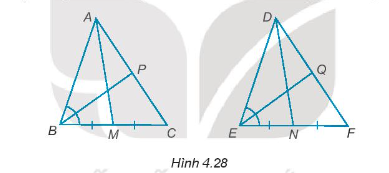
Bài 4.28 trang 62 SBT Toán 7 Tập 1: Cho tam giác ABC bằng tam giác DEF (H.4.28).

a) Gọi M và N lần lượt là trung điểm các đoạn thẳng BC và EF. Chứng minh rằng AM = DN.

b) Trên hai cạnh AC và DF lấy hai điểm P và Q sao cho BP, EQ lần lượt là phân giác của các góc $\hat{A B C}$ và $\hat{D E F}$ . Chứng minh rằng: BP = EQ.

Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

a) Vì ∆ABC = ∆DEF nên

$\{\begin{cases} \hat{A B C} = \hat{D E F}; \hat{B A C} = \hat{E D F}; \\ \hat{A C B} = \hat{D F E} \\ A B = D E; B C = E F; A C = D F \end{cases}$

Vì M là trung điểm của BC nên BM = MC = $\frac{1}{2} B C$ .

Vì N là trung điểm của EF nên EN = NF = $\frac{1}{2} E F$ .

Mà BC = EF (chứng minh trên) nên BM = EN.

Xét ∆ABM và ∆DEN ta có:

BM = EN (chứng minh trên)

AB = DE (chứng minh trên)

$\hat{A B M} = \hat{D E N}$ (do $\hat{A B C} = \hat{D E F}$ chứng minh trên)

Do đó, ∆ABM = ∆DEN (c – g – c).

Suy ra, AM = DN (hai cạnh tương ứng).

b) Vì BP là tia phân giác của góc $\hat{A B P}$ nên $\hat{A B P} = \hat{P B C} = \frac{\hat{A B C}}{2}$

Vì EQ là tia phân giác của góc $\hat{D E F}$ nên $\hat{D E Q} = \hat{Q E F} = \frac{\hat{D E F}}{2}$

Mà $\hat{A B C}$ = $\hat{D E F}$ nên $\hat{P B C}$ = $\hat{Q E F}$ .

Xét ∆PBC và ∆QEF ta có:

BC = EF (chứng minh trên)

$\hat{P B C}$ = $\hat{Q E F}$ (chứng minh trên)

$\hat{P C B} = \hat{Q F E}$ (do $\hat{A C B} = \hat{D F E}$ chứng minh trên)

Do đó, ∆PBC = ∆QEF (g – c – g)

Suy ra, BP = EQ (hai cạnh tương ứng).

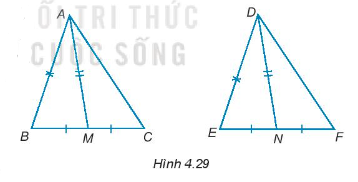
Bài 4.29 trang 62 SBT Toán 7 Tập 1: Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF. Giả sử rằng AB = DE, BC = EF, AM = DN (H.4.29). Chứng minh rằng ∆ABC = ∆DEF.

Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

Vì M là trung điểm của BC nên BM = MC = $\frac{B C}{2}$

Vì N là trung điểm của EF nên EN = NF = $\frac{E F}{2}$

Mà BC = EF (giả thiết) nên BM = EN.

Xét ∆ABM và ∆DEN ta có:

AB = DE (giả thiết)

BM = EN (chứng minh trên)

AM = DN (giả thiết)

Do đó, ∆ABM = ∆DEN (c – c – c).

Suy ra, $\hat{A B M} = \hat{D E N}$ (hai góc tương ứng) hay $\hat{A B C} = \hat{D E F}$ .

Xét ∆ABC và ∆DEF ta có:

AB = DE (giả thiết)

BC = EF (giả thiết)

$\hat{A B C} = \hat{D E F}$ (chứng minh trên)

Do đó, ∆ABC = ∆DEF (c – g – c).

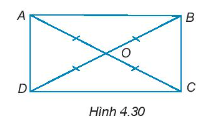
Bài 4.30 trang 62 SBT Toán 7 Tập 1:Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như Hình 4.30. Chứng minh ABCD là hình chữ nhật.

Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)