Bài tập về Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song chọn lọc

Quý Lê Xuân Ngày: 08-03-2024 Lớp 10

Tải xuống 5 3.9 K 43

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song lớp 10, tài liệu bao gồm 5 trang đầy đủ lý thuyết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Bài tập Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song gồm các nội dung chính sau:

A. Lý thuyết

- tóm tắt lý thuyết ngắn gọn.

B. Bài tập tự luyện

- gồm 33 bài tập tự luyện giúp học sinh tự rèn luyện cách giải các dạng Bài tập Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Bài tập Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song (ảnh 1)

KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN ĐƯỜNG THẲNG, HAI ĐƯỜNG THẲNG SONG SONG

A. LÝ THUYẾT

Khoảng cách:

• Khoảng cách từ điểm $M (x_{M}; y_{M})$ đến $Δ : A x + B y + C = 0$ là:

$M H = d (M, Δ) = \frac{|A x_{M} + B y_{M} + C|}{\sqrt{A^{2} + B^{2}}}$

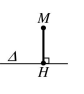
Bài tập Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song (ảnh 2)

Chú ý: $d (M, O x) = |y_{M}|, d (M, O y) = |x_{M}|$

• Khoảng cách giữa hai đường thẳng $Δ_{1}$ và $Δ_{2}$

Nếu $Δ_{1}$ và cắt hoặc trùng nhau thì $d (Δ_{1}, Δ_{2}) = 0$

Nếu $Δ_{1} / / Δ_{2}$ thì $d (Δ_{1}, Δ_{2}) = d (M, Δ_{2}) = M H$ với $M \in Δ_{1}$

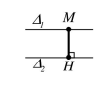
Bài tập Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song (ảnh 3)

Chú ý:

Cho hai đường thẳng song song $Δ_{1}$ và $Δ_{2}$

Biết $Δ_{1} : A_{1} x + B_{1} y + C_{1} = 0$ và $Δ_{2} : A_{2} x + B_{2} y + C_{2} = 0$

Đường thẳng $Δ_{3}$ song song và cách đều $Δ_{1}$ và $Δ_{2}$ có dạng:

$A x + B y + \frac{C_{1} + C_{2}}{2} = 0$

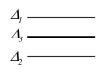
B. BÀI TẬP TỰ LUYỆN

Câu 1. Trong mặt phẳng với hệ tọa độ $O x y$ , cho điểm $M (x_{0}; y_{0})$ và đường thẳng $Δ : a x + b y + c = 0$ . Khoảng cách từ điểm M đến $Δ$ được tính bằng công thức: