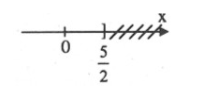Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề bất phương trình bậc nhất một ẩn, tài liệu bao gồm 15 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu gồm có:

I. Lý thuyết

II. Bài tập minh hoạ

Chuyên đề Bất phương trình bậc nhất một ẩn

A. Bài giảng

1. Định nghĩa

Định nghĩa: Bất phương trình dạng:

\(ax + b > 0,\,ax + b < 0,\,ax + b \le 0,\,ax + b \ge 0.\)

Với a và b là hai số đã cho và \(a \ne 0\), được gọi là bất phương trình bậc nhất một ẩn.

2. Hai quy tắc biến đổi bất phương trình

a. Quy tắc chuyển về

Với các bất đẳng thức, ta có thể biến đối:

\(a + b < c \Leftrightarrow a + b - c < 0 \to \) chuyển vế và đổi dấu.

Và với các bất phương trình chúng ta cũng có được những quy tắc như vậy, cụ thể:

Quy tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu hạng tử đó.

Sử dụng quy tắc trên, bước đầu chúng ta có thể giải được một vài bất phương trình đơn giản, thí dụ sau sẽ minh hoạ điều này.

Ví dụ 1. Sử dụng quy tắc chuyển vế giải các bất phương trình và và hãy biểu diễn tập nghiệm của nó trên trục số:

a, x + 3 < 4

b. 3x \( \ge \) 2x – 2

Giải

a. Sử dụng quy tắc chuyển về, biến đổi phương trình về dạng:

\(x + 3 < 4 \Leftrightarrow x < 4 - 3 \Leftrightarrow x < 1\)

Vậy, bất phương trình có nghiệm x < 1 và ta có biểu diễn:

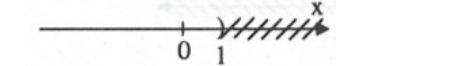
b. Sử dụng quy tắc chuyển vế, biến đổi phương trình về dạng:

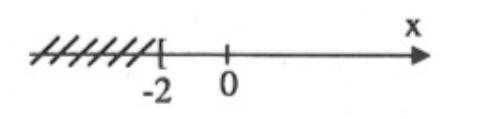
\(\begin{array}{l}3x \ge 2 - 2 \Leftrightarrow 3x - 2x \ge  - 2\\ \Leftrightarrow x \ge  - 2\end{array}\)

Vậy, bất phương trình có nghiệm \(x \ge  - 2\) và ta có biểu diễn:

Ví dụ 2. Giải các bất phương trình sau:

a. x + 12 > 21

b. -2x > -3x – 5

Giải

a. Ta có biến đổi \(x + 12 > 21 \Leftrightarrow x > 21 - 12 \Leftrightarrow x = 9\)

Vây, bất phương trình có nghiệm x > 9.

b. Ta có biến đổi: \( - 2x >  - 3x - 5 \Leftrightarrow 3x - 2x >  - 5 \Leftrightarrow x >  - 5\)

Vậy, bất phương trình có nghiệm x > -5

b. Quy tắc nhân với một số

Với các bất đẳng thức, ta có thể biến đổi:

 \(2x + 4b >  - 2 \Leftrightarrow 1 + 2b >  - 1 \to \) nhân cả hai vế với \(\frac{1}{2} > 0\) (hoặc chia cả hai vế cho 2 > 0)

\( - 3a < 6 \Leftrightarrow a >  - 2 \to \) nhân cả hai vế với \( - \frac{1}{3} < 0\) (hoặc chia vả hai vế cho -3 < 0).

Và với các bất phưởng trình chúng ta cũng có được quy tắc như vậy, cụ thể:

Quy tắc nhân với một số: Khi nhân (hoặc chia) cả hai vế của bất phương trình với cùng một khác 0, ta phải:

1. Giữ nguyên chiều của bất phương trình nếu số đó dương.

2. Đổi chiều của bất phương trình nếu số đó âm.

Sử dụng quy tắc trên, bước đầu chúng ta có thể giải được một bài bất phương trình đơn giản, thí dụ sau sẽ minh hoạ điều này.

Ví dụ 3. Sử dụng quy tắc nhân với một số giải các bất phương trình sau và hãy biểu diễn tập nghiệm của nó trên trục số:

a. 3x < -6

b. \( - \frac{1}{2}x \ge  - 2\)

Giải

a. Sử dụng quy tắc nhân với một số, biến đổi phương trình về dạng:

\(3x <  - 6 \Leftrightarrow x <  - 2\)

Vậy, bất phương trình có nghiệm x < -2 và ta có biểu diễn:

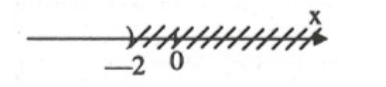
b. Sử dụng quy tắc nhân với một số, biến đổi phương trình về dạng:

\( - \frac{1}{2}x \ge  - 2 \Leftrightarrow x \le 4\)

Vậy, bất phương trình có nghiệm \(x \le 4\) và ta có biểu diễn:

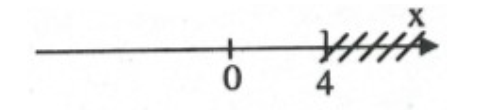
Ví dụ 4. Giải các bất phương trình sau:

a. 2x < 24

b. -3x < 27

Giải

a. Ta có biến đổi:

\(2x < 24 \Leftrightarrow x < 12\)

Vậy, bất phương trình có nghiệm x < 12

b. Ta có biến đổi:

\( - 3x < 27 \Leftrightarrow x >  - 9\)

Vậy, bất phương trình có nghiệm x > -9

Chú ý: Tiếp theo, chúng ta minh hoạ việc sử dụng đồng thời hai quy tắc biến đổi bất phương trình để bước đầu làm quen với việc giải một bất phương trình.

Ví dụ 5. Sử dụng hai quy tắc biến đổi bất phương trình để giải các bất phương trình sau:

a. 3x > x + 8

b. x² + 2x > x² – 4

Giải

a. Sử dụng lần lượt các quy tắc , biến đổi bất phương trình về dạng:

\(3x - x > 8 \Leftrightarrow 2x > 8 \Leftrightarrow x > 4\)

Vậy, bất phương trình có nghiệm x > 4

b. Sử dụng lần lượt các quy tắc , biến đổi bất phương trình về dạng:

\(\begin{array}{l}{x^2} + 2x > {x^2} - 4\\ \Leftrightarrow {x^2} + 2x - {x^2} >  - 4 \Leftrightarrow x >  - 2\end{array}\)

Vậy, bất phương trình có nghiệm x > -2

Nhận xét:

1. Trong lời giải các bất phương trình trên, chúng ta đã thừa nhận rằng kết quả “ Từ một bất phương tình, dùng quy tắc chuyển vế hay quy tắc nhân, ta luôn nhận được một bất phương trình mới tương đương với bất phương trình đã cho”.

2. Cũng chính nhờ những quy tắc này mà việc chứng minh một bắt đẳng thức sẽ đơn giản hơn rất nhiều – Điều này chúng ta sẽ gặp lại trong chủ đề chuyên sâu về bất đẳng thức ở cuối chương.

3. Giải bất phương trình bậc nhất một ẩn

Bất phương tình bậc nhất một ẩn dạng:

ax + b > 0, \(a \ne 0\)

Được giải như sau: \(ax + b > 0 \Leftrightarrow ax >  - b\)

Với a > 0, ta được \(x >  - \frac{b}{a}\)

Với a < 0, ta được \(x <  - \frac{b}{a}\)

Ví dụ 6. Giải bất phương trình -4x – 8 < 0 và biểu diễn tập nghiệm trên trục số.

Giải

Ta có biến đổi:

\( - 4x - 8 < 0 \Leftrightarrow 4x >  - 8 \Leftrightarrow x >  - 2\)

Vậy, bất phương trình có nghiệm x > -2 ta có biểu diễn:

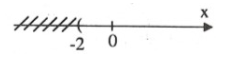
B. Bài tập minh hoạ

Dạng 1: Điều kiện để một bất phương trình là bất phương trình bậc nhất một ẩn

Ví dụ 1. Tìm điều kiện của tham số m để bất phương trình sau là bất phương trình bậc nhất một ẩn:

\(a.\,\left( {{m^2} - 2m} \right){x^2} + mx + 3 > 0\)

\(b.\,mx + \left( {m - 1} \right)y + 4 \le 0\)

Giải

a. Để bất phương trình \(\,\left( {{m^2} - 2m} \right){x^2} + mx + 3 > 0\) là bất phương trình bậc nhất một ẩn khi và chỉ khi:

\(\left\{ \begin{array}{l}{m^2} - 2m = 0\\m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m\left( {m - 2} \right) = 0\\m \ne 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m = 0\,\,or\,m = 2\\m \ne 0\end{array} \right. \Leftrightarrow m = 2\)

Vậy, với m = 2 bất phương trình đã cho là bất phương trình bậc nhất một ẩn x.

b. Để bất phương trình \(mx + \left( {m - 1} \right)y + 4 \le 0\) là bất phương trình bậc nhất một ẩn có hai trường hợp:

Trường hợp 1: Nó là bất phương trình bậc nhất một ẩn x khi và chỉ khi:

\(\left\{ \begin{array}{l}m \ne 0\\m - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m = 1\end{array} \right. \Leftrightarrow m = 1\)

Trường hợp 2: Nó là bất phương trình bậc nhất một ẩn y khi và chỉ khi:

\(\left\{ \begin{array}{l}m = 0\\m - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 0\\m \ne 1\end{array} \right. \Leftrightarrow m = 0\)

Kết luận:

Với m = 1 bất phương trình đã cho là bất phương trình bậc nhất một ẩn x.

Với m = 0 bất phương tình đã cho là bất phương trình bậc nhất một ẩn y.

Dạng 2: Giải bất phương trình bậc nhất một ẩn

Ví dụ 1: Giải các bật phương trình (theo quy tắc chuyển vế)

a. x – 5 > 3

b. x – 2x < -2x + 4

c. -3x > -4x + 2

d. 8x +2 < 7x – 1

Giải

a. Ta có:

\(x - 5 > 3 \Leftrightarrow x > 3 + 5 \Leftrightarrow x > 8\)

Vậy, nghiệm của bất phương trình là x > 8

b. Ta có:

\(x - 2x <  - 2x + 4 \Leftrightarrow x - 2x + 2x < 4 \Leftrightarrow x < 4\)

Vậy, nghiệm của bất phưởng trình là x < 4

c. Ta có:

\( - 3x >  - 4x + 2 \Leftrightarrow  - 3x + 4x > 2 \Leftrightarrow x > 2\)

Vậy, nghiệm của bất phương trình là x > 2

d. Ta có:

\(8x + 2 < 7x - 1 \Leftrightarrow 8x - 7x <  - 1 - 2 \Leftrightarrow x <  - 3\)

Vậy, nghiệm của bất phương trình là x < -3

Ví dụ 2. Giải các phương trình (theo quy tắc nhân):

a. 0,3x > 0,6

b. -4x < 12

c. -x > 4

d. 1,5x > -9

Giải

a. Ta có: \(0,3x > 0,6 \Leftrightarrow 0,3x.\frac{1}{{0,3}} > 0,6\)

\( \Leftrightarrow x > \frac{{0,6}}{{0,3}} \Leftrightarrow x > 2\)

Vậy, nghiệm của bất phương trình là x > 2.

b. Ta có:

\(\begin{array}{l} - 4x < 12 \Leftrightarrow \left( { - 4x} \right).\left( {\frac{1}{4}} \right) > 12.\left( { - \frac{1}{4}} \right)\\ \Leftrightarrow x >  - 3.\end{array}\)

Vậy, nghiệm của bất phương trình là x > -3.

c. Ta có: \( - x > 4 \Leftrightarrow \left( { - x} \right)\left( { - 1} \right) < 4.\left( { - 1} \right) \Leftrightarrow x <  - 4\).

Vậy, nghiệm của bất phương trình là x < -4.

d. Ta có: \(1,5x >  - 9 \Leftrightarrow 1,5x.\frac{1}{{1,5}} > \left( { - 9} \right).\frac{1}{{1,5}} \Leftrightarrow x >  - 6.\)

Vậy, nghiệm của bất phương trình là x > -6.

Ví dụ 3. Giải các bất phương trình sau và hãy biểu diễn tập nghiệm của nó trên trục số:

a. 2x – 3 > 0

b. 3x + 4 < 0

\(c. 4 - 3x  \le  0\)

\(d. 5  -  2x  \ge  0\)

Giải

a. Ta biến đổi:

\(2x - 3 > 0 \Leftrightarrow 2x > 3 \Leftrightarrow x > \frac{3}{2}\)

Vậy, nghiệm của bất phương trình là \(x > \frac{3}{2}\) và ta có biểu diễn.

b. Ta có biến đổi

\(3x + 4 < 0 \Leftrightarrow 3x <  - 4 \Leftrightarrow x <  - \frac{3}{4}\)

Vậy, nghiệm của bất phương trình là \(x >  - \frac{4}{3}\) và ta có biểu diễn.

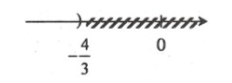
c. Ta có biến đổi:

\(4 - 3x \le 0 \Leftrightarrow 3x \ge 4 \Leftrightarrow x \ge \frac{4}{3}\)

Vậy, nghiệm của bất phương trình là \(x \ge \frac{4}{3}\) và ta có biểu diễn.

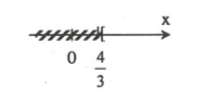
d. Ta có biến đổi:

\(5 - 2x \ge 0 \Leftrightarrow 2x \le 5 \Leftrightarrow x \le \frac{5}{2}\)

Vậy, nghiệm của bất phương trình là \(x \le \frac{5}{2}\) và ta có biểu diễn.