Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 3 Bài 3:Phương trình đưa được về dạng ax + b = 0. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 3:Phương trình đưa được về dạng ax + b = 0 .Mời các bạn đón xem:
Bài tập Toán 8 Chương 3 Bài 3: Phương trình đưa được về dạng ax + b = 0
A, Bài tập Phương trình đưa được về dạng ax + b = 0
I. Bài tập trắc nghiệm
Bài 1: Nghiệm của phương trình 4( x - 1 ) - ( x + 2 ) = - x là?
A. x = 2.
B. x = .
C. x = 1.
D. x = - 1.
Lời giải:
Ta có: 4( x - 1 ) - ( x + 2 ) = - x
⇔ 4x - 4 - x - 2 = - x
⇔ 4x - x + x = 2 + 4 ⇔ 4x = 6 ⇔ x = .
Vậy phương trình đã cho có nghiệm là x = .
Chọn đáp án B.
Bài 2: Nghiệm của phương trình là?
A. x = 0.
B. x = 1.
C. x = 2.
D. x = 3.
Bài 3: Tập nghiệm của phương trình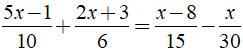
A. S = { }.
B. S = { }
C. S = { }.
D. S = { }.
Ta có:
⇔ 15x - 3 + 10x + 15 = 2x - 16 - x
⇔ 25x - 2x + x = - 16 - 15 + 3
⇔ 24x = - 28 ⇔ x = .
Vậy phương trình đã cho có tập nghiệm là S = { }.
Chọn đáp án C.
Bài 4: Nghiệm của phương trình - 10( 2,3 - 3x ) = 5( 3x + 1 ) là?
A. x = 1,2
B. x = - 1,2
C. x = -
D. x =
Ta có: - 10( 2,3 - 3x ) = 5( 3x + 1 )
⇔ - 23 + 30x = 15x + 5
⇔ 30x - 15x = 5 + 23
⇔ 15x = 28 ⇔ x = .
Vậy phương trình đã cho có nghiệm là x =
Chọn đáp án D.
Bài 5: Nghiệm của phương trình là?
A. x = - .
B. x = .
C. x = - 1.
D. x = - .
Ta có:
⇔ 15x + 15 + 15 - 20 = 30x + 20 + 16x + 20
⇔ 31x = - 30 ⇔ x = - .
Vậy phương trình đã cho có nghiệm là x = - .
Chọn đáp án A.
Bài 6: Giải phương trình 3(2x + 4) - 2x = x - 2(3 - x)
A. x = -18
B.x = 10
C. x = - 6
D. x = 19
Chọn đáp án A
Bài 7: Giải phương trình: x - 4(x - 10) = 1 – 2(x + 3)
A. x = 45
B. x = 15
C. x = - 15
D. x = - 40
Chọn đáp án A
Bài 8: Giải phương trình:
A. x = -1
B. x = -2
C. x = 2
D. x = 1
Chọn đáp án D
Bài 9: Giải phương trình (2x – 2)2 + 10 = 4x2 + 2x - 8
Chọn đáp án B
Bài 10: Giải phương trình:
Chọn đáp án A
II. Bài tập tự luận có lời giải
Bài 1: Tìm điều kiện của m để phương trình (3m – 4)x + m = 3m2 + 1 có nghiệm duy nhất.
Lời giải
Xét phương trình (3m – 4)x + m = 3m2 + 1 có a – 3m – 4
Để phương trình có nghiệm duy nhất thì a ≠ 0 ⇔ 3m – 4 ≠ 0
Bài 2 Số nguyên dương nhỏ nhất của m để phương trình (3m – 3)x + m = 3m2 + 1 có nghiệm duy nhất là?
Lời giải
Xét phương trình (3m – 3)x + m = 3m2 + 1 có a = 3m – 3
Để phương trình có nghiệm duy nhất thì a ≠ 0 ⇔ 3m – 3 ≠ 0
⇔ 3m ≠ 3 ⇔ m ≠ 1
Vậy m ≠ 1, mà m là số nguyên dương nhỏ nhất nên m = 2
Bài 3 Phương trình có nghiệm là?
Lời giải
Bài 4 Phương trình 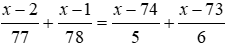
Lời giải
Vậy phương trình có nghiệm duy nhất x = 79
Bài 5 Nghiệm của phương trình là?
Lời giải
Vậy phương trình có nghiệm x = -(a + b + c)
Bài 6 Giải phương trình:
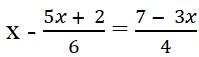
Lời giải
Vậy phương trình có một nghiệm duy nhất x =
Bài 7 Tìm chỗ sai và sửa lại các bài giải sau cho đúng:
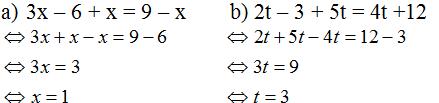
Lời giải:
a) Sai ở phương trình thứ hai khi chuyển vế hạng từ -6 từ vế trái sang vế phải, hạng tử -x từ vế phải sang vế trái mà không đổi dấu.
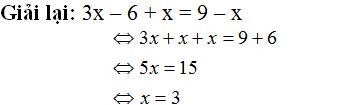
Vậy phương trình có nghiệm duy nhất x = 3.
b) Sai ở phương trình thứu hai, chuyển vế hạng từ -3 từ vế trái sang vế phải mà không đổi dấu.
Giải lại:
2t - 3 + 5t = 4t + 12
⇔ 2t + 5t - 4t = 12 + 3
⇔ 3t = 15
⇔ t = 5
Vậy phương trình có nghiệm duy nhất t = 5
Bài 8 Giải các phương trình:
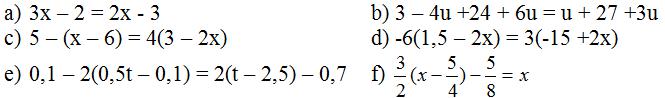
Lời giải:
a) 3x – 2 = 2x – 3
⇔ 3x – 2x = -3 + 2
⇔ x = -1.
Vậy phương trình có nghiệm x = -1.
b) 3 – 4u + 24 + 6u = u + 27 + 3u
⇔ -4u + 6u – u – 3u = 27 – 3 – 24
⇔ -2u = 0
⇔ u = 0.
Vậy phương trình có nghiệm u = 0.
c) 5 – (x – 6) = 4.(3 – 2x)
⇔ 5 – x + 6 = 12 – 8x
⇔ -x + 8x = 12 – 5 – 6
⇔ 7x = 1
⇔
Vậy phương trình có nghiệm
d) -6(1,5 – 2x) = 3(-15 + 2x)
⇔ -6.1,5 + (-6).(-2x) = 3.(-15) + 3.2x
⇔ -9 + 12x = -45 + 6x
⇔ 12x – 6x = -45 + 9
⇔ 6x = -36
⇔ x = -6.
Vậy phương trình có nghiệm x = -6.
e) 0,1 – 2(0,5t – 0,1) = 2(t – 2,5) – 0,7
⇔ 0,1 – 2.0,5t + 2.0,1 = 2t – 2.2,5 – 0,7
⇔ 0,1 – t + 0,2 = 2t – 5 – 0,7
⇔ 0,1 + 0,2 + 5 + 0,7 = 2t + t
⇔ 6 = 3t
⇔ t = 2.
Vậy phương trình có nghiệm t = 2.
Vậy phương trình có nghiệm x = 5.
Bài 9 Giải các phương trình:
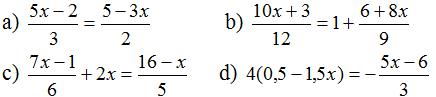
Lời giải:
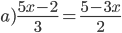
⇔2(5x - 2) = 3(5 - 3x)
⇔10x - 4 = 15 - 9x
⇔10x + 9 = 15 + 4
⇔19x = 19
⇔x = 1
Vậy x = 1
![]()
⇔30x + 9 = 36 = 24 + 32x
⇔30x - 32x = 60 - 9
⇔-2x = 51
⇔x = -25.5
Vậy x = -25.5
![]()
⇔5(7x - 1) + 60x = 6(16 - x)
⇔35x - 5 + 6x = 96 - 6x
⇔35x + 60x + 6x = 96 + 5
⇔101x = 101
⇔x = 1
Vậy x = 1
![]()
⇔6 - 18x = -5x + 6
⇔-18x + 5x = 0
⇔-13x = 0
⇔x = 0
Vậy x = 0
III. Bài tập vận dụng
Bài 1 Bạn Hòa giải phương trình x(x + 2) = x(x + 3) như trên hình. Theo em, bạn Hòa giải đúng hay sai?

Em sẽ giải phương trình đó như thế nào?
Bài 2 Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ôtô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Hãy viết phương trình biểu thị việc ôtô gặp xe máy sau x giờ, kể từ khi ôtô khởi hành.
Bài 3 Viết phương trình biểu thị cân thăng bằng trong hình 3 (đơn vị khối lượng là gam).
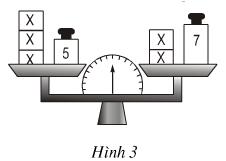
Bài 4 Giải phương trình:
![]()
Bài 5 Tìm chỗ sai và sửa lại các bài giải sau cho đúng:
a.
b.
Bài 6 Giải các phương trình:
a) (\3x-2=2x-3\)
b)
c)
d)
e)
f)
Bài 7 Giải các phương trình
a)
b)
c)
d)
Bài 8 Giải các phương trình:
a)
b)
Bài 9 Viết phương trình ẩn x rồi tính x (mét) trong mỗi hình dưới đây
(S là diện tích của hình)

Bài 10 Trung bảo Nghĩa hãy nghĩ ở trong đầu một sô tự nhiên tùy ý, sau đó Nghĩa thêm 5 vào số ấy, nhân tổng nhận được với 2, được bao nhiêu đem trừ đi 10, tiếp tục nhân hiệu tìm được với 3 rồi cộng thêm 66, cuối cùng chia kết quả cho 6. Chẳng hạn, nếu Nghĩa nghĩ đến số 7 thì quá trình tính toán sẽ là: 7 → (7 + 5= 12) →(12x2=24) →(24 – 10 = 14) → (14 x 3 = 42) → (42 + 66 = 108) → (108 : 6 = 18)
Trung chỉ cần biết kết quả cuối cùng (số 18) là đoán ngay được số Nghĩa đã nghĩ là số nào.
Nghĩa thử mấy lần, Trung đều đoán đúng. Nghĩa phục tài Trung lắm. Đố em tìm ra bí quyết của Trung đấy?
B. Lý thuyết Phương trình đưa được về dạng ax + b = 0
Cách giải phương trình đưa được về dạng ax + b = 0: Để giải các phương trình đưa được về ax + b = 0, ta thường biến đổi phương trình như sau:
Bước 1: Quy đồng mẫu hai vế và khử mẫu (nếu có).
Bước 2: Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax = c.
Bước 3: Tìm x.
Chú ý: Quá trình biến đổi phương trình về dạng ax = c có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0 nếu:
0x = c thì phương trình vô nghiệm S = .
0x = 0 thì phương trình nghiệm đúng với mọi x hay vô số nghiệm S = .
Ví dụ 1. Giải phương trình: 4(x + 6) = 2x – 8.
Lời giải:
4(x + 6) = 2x – 8
4x + 24 = 2x – 8
4x – 2x = –24 – 8
2x = –32
x = –32 : 2
x = –16.
Vậy phương trình có tập nghiệm là S = {–16}.
Ví dụ 2. Giải phương trình: .
Lời giải:
2(x + 1)(3x – 1) – (6x2 + 2) = 20
(6x2 + 4x –2) – (6x2 + 2) = 20
6x2 + 4x –2 – 6x2 – 2 = 20
4x = 20 + 2 + 2
4x = 24
x = 6.
Vậy phương trình có tập nghiệm là S = {6}.