Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Ôn tập chương 3 Đại số hay, chi tiết giúp học sinh dễ dàng làm bài tập Ôn tập chương 3 Đại số lớp 8.

Giải bài tập Toán lớp 8 Ôn tập chương 3 Đại số

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 32 Toán 8 Tập 2: Thế nào là hai phương trình tương đương?

Trả lời:

Hai phương trình tương đương là hai phương trình có cùng một tập nghiệm.

Câu hỏi 2 trang 32 Toán 8 Tập 2: Nhân hai vế của một phương trình với cùng một biểu thức chứa ẩn thì có thể không được phương trình tương đương. Em hãy cho một ví dụ.

Trả lời:

Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S₁ = {4}.

Nhân hai vế của phương trình (1) với x, ta được phương trình:

(x - 1)x = 3x (2)

⇔ (x - 1)x - 3x = 0

⇔ x(x - 4) = 0

Suy ra: x = 0 hoặc x – 4 = 0

Nếu x – 4 = 0 thì x = 4.

Phương trình (2) có tập nghiệm là S₂ = {0, 4}.

Vì S₁ ≠ S₂ nên hai phương trình (1) và (2) không tương đương.

Câu hỏi 3 trang 32 Toán 8 Tập 2: Với điều kiện nào của a thì phương trình ax + b = 0 là một phương trình bậc nhất? (a và b là hai hằng số).

Trả lời:

Với điều kiện a ≠ 0 thì phương trình ax + b = 0 là một phương trình bậc nhất.

Câu hỏi 4 trang 32 Toán 8 Tập 2: Một phương trình bậc nhất một ẩn có mấy nghiệm? Đánh dấu "x" vào ô vuông ứng với câu trả lời đúng:

$\boxed{}$ Vô nghiệm

$\boxed{}$ Luôn có nghiệm

$\boxed{}$ Có vô số nghiệm

$\boxed{}$ Có thể vô nghiệm, có thể có một nghiệm duy nhất và cũng có thể có vô số nghiệm

Trả lời:

Ô vuông thứ 2: Một phương trình bậc nhất một ẩn luôn có một nghiệm duy nhất.

Chú ý vì đây là phương trình bậc nhất một ẩn nên a ≠ 0, do đó phương trình luôn có một nghiệm duy nhất. Không có trường hợp a = 0.

Câu hỏi 5 trang 33 Toán 8 Tập 2: Khi giải phương trình chứa ẩn ở mẫu, ta phải chú ý điều gì?

Trả lời:

Khi giải phương trình chứa ẩn ở mẫu, ta phải chú ý đến điều kiện xác định của phương trình.

Câu hỏi 6 trang 33 Toán 8 Tập 2: Hãy nêu các bước giải bài toán bằng cách lập phương trình.

Trả lời:

Bước 1. Lập phương trình.

- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không thỏa mãn, rồi kết luận.

Bài tập (trang 33; 34)

Bài 50 trang 33 Toán 8 Tập 2: Giải các phương trình:

a) 3 - 4x(25 – 2x) = 8x² + x – 300.

b) $\frac{2(1-3x)}{5}-\frac{2+3x}{10}=7-\frac{3(2x+1)}{4}$;

c) $\frac{5x+\text{\hspace{0.17em}}2}{6}-\frac{8x-1}{3}=\frac{4x+\text{}2}{5}-5$;

d) $\frac{3x+\text{\hspace{0.17em}}2}{2}-\frac{3x+1}{6}=2x+\frac{5}{3}$.

Lời giải:

a) 3 – 4x(25 – 2x) = 8x² + x – 300

⇔ 3 – 4x.25 + 4x.2x = 8x² + x – 300

⇔ 3 – 100x + 8x² = 8x² + x – 300

⇔ -101x = -303

⇔ x = 3.

Vậy phương trình có tập nghiệm S = {3}.

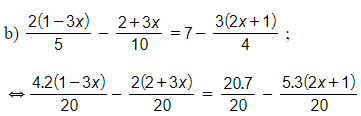
⇔ 8(1- 3x)  - 2(2 + 3x) = 140 – 15(2x + 1)

⇔ 8 - 24x – 4 – 6x = 140 – 30x – 15

⇔ -24x – 6x + 30x = 140 – 15 – 8 + 4

⇔ 0x = 121 (vô lý)

Vậy phương trình vô nghiệm.

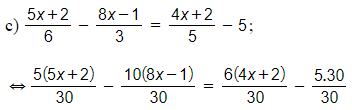
⇔ 5(5x + 2) – 10(8x – 1) = 6(4x + 2) – 150

⇔ 25x + 10 – 80x + 10 = 24x + 12 – 150

⇔ 20 – 55x = 24x – 138

⇔ -55x – 24x = -138 – 20

⇔ -79x = -158

$\iff x=(-158):(-79)$

⇔ x = 2.

Vậy phương trình có tập nghiệm S = {2}.

d) 

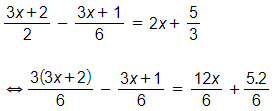
⇔ 3(3x + 2) – (3x + 1) = 12x + 10

⇔ 9x + 6 – 3x – 1 = 12x + 10

⇔ 6x + 5 = 12x + 10

⇔ 6x – 12x = 10 – 5

⇔ -6x = 5

⇔ $x=\frac{-5}{6}$

Vậy phương trình có tập nghiệm  $S=\left\{\frac{-5}{6}\right\}$.

Bài 51 trang 33 Toán 8 Tập 2: Giải các phương trình sau bằng cách đưa về phương trình tích:

a) (2x + 1)(3x – 2) = (5x – 8)(2x + 1);

b) 4x² – 1 = (2x + 1)(3x – 5);

c) (x + 1)² = 4(x² - 2x + 1);

d) 2x³ + 5x² – 3x = 0.

Lời giải:

a) (2x + 1)(3x – 2) = (5x – 8)(2x + 1)

⇔ (2x + 1)(3x – 2) – (5x – 8)(2x + 1) = 0

⇔ (2x + 1).[(3x – 2) – (5x – 8)] = 0

⇔ (2x + 1).(3x – 2 – 5x + 8) = 0

⇔ (2x + 1)(6 – 2x) = 0

⇔ 2x + 1 = 0 hoặc 6 – 2x = 0

 Nếu  2x + 1 = 0 ⇔ 2x = -1 ⇔ x = $\frac{-1}{2}$.

 Nếu  6 – 2x = 0 ⇔ 6 = 2x ⇔ x = 3.

Vậy phương trình có tập nghiệm  $S\text{\hspace{0.17em}\hspace{0.17em}}=\left\{\frac{-1}{2};3\right\}$.

b) 4x² – 1 = (2x + 1)(3x – 5)

⇔ 4x² – 1 – (2x + 1)(3x – 5) = 0

⇔ (2x – 1)(2x + 1) – (2x + 1)(3x – 5) = 0

⇔ (2x + 1)[(2x – 1) – (3x – 5)] = 0

⇔ (2x + 1)(2x – 1 – 3x + 5) = 0

⇔ (2x + 1)(4 – x) = 0

⇔ 2x + 1= 0 hoặc 4 – x = 0

Nếu 2x + 1 = 0 ⇔ 2x = -1 ⇔ $x=\frac{-1}{2}$ .

 Nếu 4 – x = 0 ⇔ x = 4.

Vậy phương trình có tập nghiệm $S\text{\hspace{0.17em}\hspace{0.17em}}=\left\{\frac{-1}{2};4\right\}$ .

c)

Cách 1:

(x + 1)² = 4(x² – 2x + 1)

⇔ (x + 1)² - 4(x² – 2x + 1) = 0

⇔ (x + 1)² - 2². (x -1)² = 0

⇔ (x + 1)² – [ 2(x – 1)]² =0

⇔ [(x + 1) + 2( x - 1)].[(x + 1) - 2( x - 1)]= 0

⇔ ( x + 1 + 2x - 2)(x + 1 – 2x + 2) =0

⇔ (3x - 1)(3 - x) = 0

⇔ 3x – 1 = 0 hoặc 3 – x = 0

Nếu 3x – 1 = 0 ⇔ 3x = 1 ⇔  $x=\frac{1}{3}$.

Nếu 3 – x = 0 ⇔ x = 3

Vậy tập nghiệm của phương trình đã cho là: $S\text{\hspace{0.17em}\hspace{0.17em}}=\left\{\frac{1}{3};3\right\}$.

* Cách 2: Ta có:

(x + 1)² = 4(x² – 2x + 1)

⇔ (x + 1)² - 4(x² – 2x + 1) = 0

⇔ x² + 2x +1 - 4x² + 8x – 4 = 0

⇔ -3x² + 10x – 3 = 0

⇔ (-3x² + 9x) + (x – 3) = 0

⇔ -3x(x – 3) + ( x - 3) = 0

⇔ ( x- 3).(-3x + 1) = 0

⇔ x - 3 = 0 hoặc -3x + 1= 0

Nếu x - 3 = 0 x = 3

Nếu - 3x + 1 = 0 hay - 3x = - 1 ⇔  $x=\frac{1}{3}$

Vậy tập nghiệm của phương trình đã cho là: $S=\left\{\frac{1}{3};3\right\}$.

d) 2x³ + 5x² – 3x = 0

⇔ x(2x² + 5x – 3) = 0

⇔ x.(2x² + 6x – x – 3) = 0

⇔ x. [2x(x + 3) – (x + 3)] = 0

⇔ x.(2x – 1)(x + 3) = 0

⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0

Nếu 2x – 1 = 0 ⇔ 2x = 1 ⇔ $x=\frac{1}{2}$.

Nếu  x + 3 = 0 ⇔ x = -3.

Vậy phương trình có tập nghiệm $S=\left\{-3;0;\frac{1}{2}\right\}$ .

Bài 52 trang 33 Toán 8 Tập 2: Giải các phương trình:

Lời giải:

a) Điều kiện xác định: x ≠ 0 và x ≠ $\frac{3}{2}$ .

$$\begin{gathered} \frac{1}{2x-3}-\frac{3}{x(2x-3)}=\frac{5}{x} \\ \iff \frac{x}{x\left(2x-3\right)}-\frac{3}{x\left(2x-3\right)}=\frac{5\left(2x-3\right)}{x\left(2x-3\right)} \\ \iff \frac{x-3}{x(2x-3)}=\frac{5(2x-3)}{x(2x-3)} \end{gathered}$$

Suy ra: x – 3 = 5(2x – 3)

⇔ x – 3 = 10x – 15

⇔ x – 10x = -15 + 3

⇔ -9x = -12

⇔$x=\frac{4}{3}$ . ( thỏa mãn điều kiện).

Vậy phương trình có tập nghiệm  $\text{}S=\left\{\frac{4}{3}\right\}$.

b) Điều kiện xác định: x ≠ 0; x ≠ 2.

$$\begin{gathered} \frac{x+2}{x-2}-\frac{1}{x}=\frac{2}{x(x-2)} \\ \iff \frac{x(x+\text{}2)-1.(x-2)}{x(x-2)}=\frac{2}{x(x-2)} \end{gathered}$$

⇒ x(x + 2) – (x – 2) = 2

⇔ x² + 2x – x + 2 = 2

⇔ x² + x = 0

⇔ x(x + 1) = 0

⇔ x = 0 hoặc x + 1 = 0.

Nếu x = 0 không thỏa mãn điều kiện xác định.

Nếu x + 1 = 0 ⇔ x = -1 (thỏa mãn điều kiện xác định).

Vậy phương trình có tập nghiệm S = {-1}.

c) Điều kiện xác định: x ≠ ±2.

⇒ (x + 1)(x + 2) + (x – 1)(x – 2) = 2(x² + 2)

⇔ x² + x + 2x + 2 + x² – x – 2x + 2 = 2x² + 4

⇔ 2x² + 4 = 2x² + 4

⇔ 0x = 0 luôn đúng với mọi x thỏa mãn điều kiện.

Vậy phương trình nghiệm đúng với mọi x ≠ ±2.

d) Điều kiện xác định: x ≠ $\frac{2}{7}$.

+ Nếu $\frac{-4x+10}{2-7x}=0$

$\Rightarrow -4x+10=0$

$\iff -4x=-10\iff x=\frac{5}{2}$ (thỏa mãn điều kiện).

+ Nếu x + 8 = 0 thì x = -8 (thỏa mãn điều kiện).

Vậy phương trình có tập nghiệm là $S\text{\hspace{0.17em}\hspace{0.17em}}=\left\{\frac{5}{2};-8\right\}$ .

Bài 53 trang 34 Toán 8 Tập 2: Giải phương trình:

$\frac{x+1}{9}+\frac{x+\text{\hspace{0.17em}\hspace{0.17em}}2}{8}=\frac{x+3}{7}+\frac{x+4}{6}$

Lời giải:

Ta có:

 $\frac{x+1}{9}+\frac{x+\text{\hspace{0.17em}\hspace{0.17em}}2}{8}=\frac{x+3}{7}+\frac{x+4}{6}$

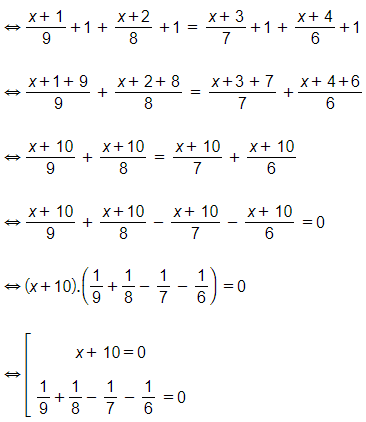
Nếu x + 10 = 0 thì  x= -10

Vì 

 $\begin{array}{l}\frac{1}{9}<\frac{1}{7};\frac{1}{8}<\frac{1}{6}\Rightarrow \frac{1}{9}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{8}<\frac{1}{7}+\text{\hspace{0.17em}}\frac{1}{6}\\ \iff \frac{1}{9}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{8}-\frac{1}{7}-\text{\hspace{0.17em}}\frac{1}{6}\text{\hspace{0.17em}\hspace{0.17em}}<0\end{array}$

Vậy phương trình có nghiệm duy nhất là x = -10.

Bài 54 trang 34 Toán 8 Tập 2: Một canô xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ bến B về bến A mất 5 giờ. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của dòng nước là 2 km/h.

Lời giải:

Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.

Vì canô xuôi dòng mất 4h nên vận tốc canô khi xuôi dòng là: $\frac{x}{4}$ (km/h)

Vì canô ngược dòng mất 5h nên vận tốc canô khi ngược dòng là $\frac{x}{5}$ (km/h).

Vận tốc dòng nước là 2km/h.

Vì khi đi xuôi dòng thì vận tốc xuôi dòng sẽ gồm vận tốc canô cộng vận tốc nước, và đi ngược dòng thì vận tốc canô bằng vận tốc thực trừ vận tốc nước nên vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước. Do đó ta có phương trình:

$\frac{x}{4}-\frac{x}{5}=2.2\iff \frac{5x-4x}{20}=\frac{80}{20}$

Suy ra: x = 80 (thỏa mãn điều kiện).

Vậy khoảng cách giữa hai bến A và B là 80 km.

(Giải thích: hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước:

Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có:

Khi xuôi dòng: vận tốc canô = v + a

Khi ngược dòng: vận tốc canô = v - a

Hiệu vận tốc = v + a - (v - a) = 2a = 2.vận tốc dòng nước.)

Bài 55 trang 34 Toán 8 Tập 2: Biết rằng 200g một dung dịch chứa 50g muối. Hỏi phải pha thêm bao nhiêu gam nước vào dung dịch đó để được một dung dịch chứa 20% muối?

Lời giải:

Gọi x (g) là khối lượng nước phải pha thêm, với x > 0.

Khối lượng dung dịch mới: 200 + x (g)

Ta có: nồng độ dung dịch = số g muối / số g dung dịch.

Vì khối lượng muối không đổi nên nồng độ dung dịch sau khi pha thêm nước bằng  $\frac{50}{x\text{\hspace{0.17em}\hspace{0.17em}}+200}$

Theo đề bài, nồng độ dung dịch mới chứa 20% muối nên ta có phương trình:

$$\begin{gathered} \begin{array}{l}\frac{50}{200+\text{\hspace{0.17em}\hspace{0.17em}}x}=20\%\\ \iff \frac{50}{200+\text{\hspace{0.17em}\hspace{0.17em}}x}=\frac{1}{5}\end{array} \\ \iff \frac{5.50}{5(200+\text{}x)}=\frac{200+\text{}x}{5(200+x)} \end{gathered}$$

Suy ra: 250 = 200 + x

$\iff x=50$  (thỏa mãn điều kiện).

Vậy phải pha thêm 50g nước để được dung dịch chứa 20% muối.

Bài 56 trang 34 Toán 8 Tập 2: Để khuyến khích tiết kiệm điện, giá điện sinh hoạt được tính theo kiểu lũy tiến, nghĩa là nếu người sử dụng càng nhiều điện thì giá mỗi số điện (1kw/h) càng tăng lên theo các mức như sau:

Mức thứ nhất: Tính cho 100 số điện đầu tiên;

Mức thứ hai: Tính cho số điện thứ 101 đến 150, mỗi số đắt hơn 150 đồng so với mức thứ nhất;

Mức thứ ba: Tính cho số điện thứ 151 đến 200, mỗi số đắt hơn 200 đồng so với mức thứ hai;

v.v...

Ngoài ra người sử dụng còn phải trả thêm 10% thuế giá trị gia tăng (thuế VAT).

Tháng vừa qua, nhà Cường dùng hết 165 số điện và phải trả 95700 đồng. Hỏi mỗi số điện ở mức thứ nhất giá là bao nhiêu?

Lời giải:

Gọi x (đồng) là giá mỗi số điện ở mức thứ nhất (x > 0).

⇒ Giá mỗi số điện ở mức 2 là: x + 150 (đồng)

⇒ Giá mỗi số điện ở mức 3 là: x + 150 + 200 = x + 350 (đồng)

Nhà Cường dùng hết 165 số điện = 100 + 50 + 15.

Như vậy nhà Cường phải đóng cho 100 số điện ở mức 1, 50 số điện ở mức 2 và 15 số điện ở mức 3.

Giá tiền 100 số điện mức đầu tiên là: 100.x (đồng)

Giá tiền 50 số điện mức thứ hai là: 50.(x + 150) (đồng)

Giá tiền 15 số điện còn lại mức thứ ba là: 15.(x + 350) (đồng).

⇒ Số tiền điện (chưa tính VAT) của nhà Cường bằng:

100.x + 50.(x + 150) + 15.(x + 350)

= 100x + 50x + 50.150 +15x +15.350

= 165x + 12750.

Thuế VAT nhà Cường phải trả là:

(165x + 12750).10% $=(\text{}165x+\text{\hspace{0.17em}}12750).\frac{10}{100}$

$\hspace{0.17em}=0,1.(\text{}165x\text{\hspace{0.17em}\hspace{0.17em}}+12750)$

Tổng số tiền điện nhà Cường phải đóng (tiền gốc + thuế) bằng:

 165x + 12750 + 0,1.(165x + 12750) = 1,1.(165x + 12750).

Thực tế nhà Cường hết 95700 đồng nên ta có phương trình:

 1,1(165x + 12750) = 95700

⇔ 165x + 12750 = 87000

⇔ 165x = 74250

⇔ x = 450 (đồng) (thỏa mãn điều kiện).

Vậy mỗi số điện ở mức giá đầu tiên là 450 đồng.