Bộ 20 Đề thi Toán lớp 8 Giữa kì 1 năm 2022

Bộ 20 Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án

Quý Lê Xuân Ngày: 08-03-2024 Lớp 8

Tải xuống 27 45.7 K 275

Tài liệu Bộ đề thi Toán lớp 8 Giữa học kì 1 có đáp án năm học 2022 - 2023 gồm 20 đề thi tổng hợp từ đề thi môn Toán 8 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Giữa học kì 1 Toán lớp 8. Mời các bạn cùng đón xem:

(Đã có) Bộ 10 đề thi giữa kì 1 Toán 8 Kết nối tri thức có đáp án năm 2023

(Đã có) Bộ 10 đề thi Giữa kì 1 Toán 8 Chân trời sáng tạo có đáp án năm 2023

(Đã có) Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án năm 2023

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 1

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 1)

Câu 1 (2 điểm) Phân tích đa thức thành nhân tử

a. 8x² - 8xy - 4x + 4y

b. x³ + 10x² + 25x - xy²

c. x² + x - 6

d. 2x² + 4x - 16

Câu 2 (2 điểm) Tìm giá trị của x, biết:

a. x³ - 16x = 0 b. (2x + 1)² - (x - 1)² = 0

Câu 3 (2 điểm) Chứng minh biểu thức sau không phụ thuộc vào x

a. A = (2x - 1)(4x² + 2x + 1) - (2x + 1)(4x² - 2x + 1)

b. B = x(2x + 1) - x²(x + 2) + x³ - x + 5

Câu 4 (1 điểm) Tính giá trị nhỏ nhất của biểu thức P = x² - 2xy + 6y² - 12x + 2y + 45

Câu 5 (2 điểm) Cho hình thang ABDC (AB // CD). Trên cạnh AD lấy điểm M và N sao cho AM = MN = NC. Từ M và N kẻ các đường thẳng song song với hai đáy cắt BC theo thứ tự E và F. Chứng minh rằng:

a. BE = EF = FD

b. Cho CD = 8cm, ME = 6cm. Tính độ dài AB và FN

Câu 6 (0.5 điểm) Cho x, y, z là các số dương. Tìm giá trị nhỏ nhất của:

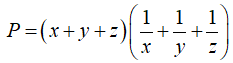
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 4)

Đáp án và Hướng dẫn làm bài

Câu 1:

a. 8x² - 8xy - 4x + 4y = 8x(x - y) - 4(x - y) = (x - y)(8x - 4) = 4(x - y)(2x - 1)

x³ + 10x² + 25x - xy² = x(x² + 10x + 25 - y²) = x[(x - 5)² - y²] = x(x - 5 - y)(x - 5 + y)

c. x² + x - 6 = x² - 2x + 3x - 6 = x(x - 2) + 3(x - 2) = (x - 2)(x + 3)

2x² + 4x - 16 = 2(x² - 2x - 8) = 2(x² - 2x + 1 - 9)

= 2[(x - 1)² - 9] = 2(x - 1 - 9)(x - 1 + 9) = 2(x - 10)(x + 8)

Câu 2:

x³ - 16x = 0

x(x² - 16) = 0

x(x - 4)(x + 4) = 0

Suy ra x = 0, x = 4, x = -4

(2x + 1)² - (x - 1)² = 0

(2x + 1 - x + 1)(2x + 1 + x - 1) = 0

(x + 2)(3x) = 0

Suy ra x = 0 hoặc x = -2

Câu 3:

A = (2x - 1)(4x² + 2x + 1) - (2x + 1)(4x² - 2x + 1)

A = (2x)³ - 1 - [(2x)³ + 1]

A = 8x³ - 1 - 8x³ - 1

A = -2

Vậy giá trị của biểu thức A không phụ thuôc vào giá trị của x.

B = x(2x + 1) - x²(x + 2) + x³ - x + 5

B = 2x² + x - x³ - 2x² + x³ - x + 5

B = 5

Vậy biểu thức không phụ thuộc vào x

Câu 4:

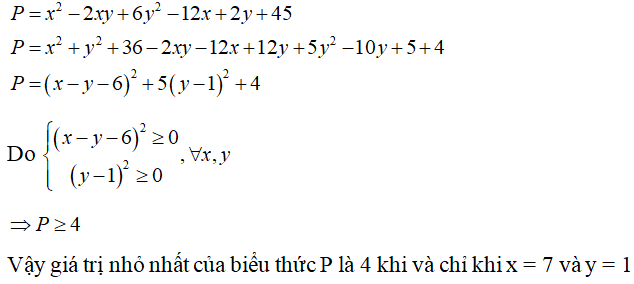
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 4)

Câu 5:

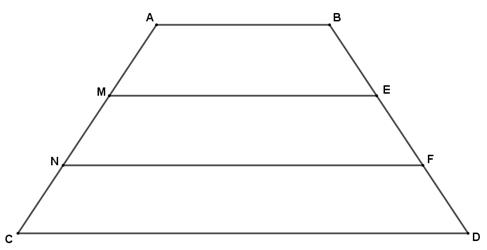
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 4)

a. Ta có ABCD là hình thang AB // CD

Ta có AB // CD, FN // CD suy ra AB // NF

Vậy ABFN là hình thang (dấu hiệu nhận biết).

Xét hình thang ABFN có ME // NF, ME = NF nên ME là đường trung bình của hình thang ABFN

Suy ra BE = EF.

Xét tương tự với hình thang MEDC ta suy ra EF = FD

Ta có điều phải chứng minh.

b. Theo chứng minh trên ta có

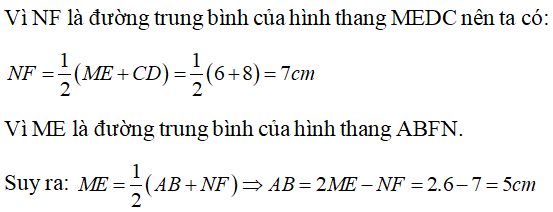
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 4)

Câu 6:

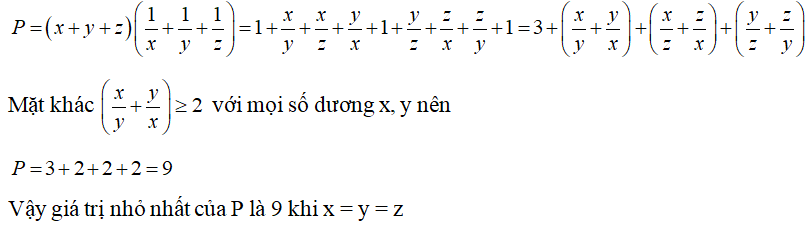
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 4)

Đề thi Toán lớp 8 Giữa kì 1 năm 2021 - 2022 có đáp án (4 Đề) (ảnh 1)

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 2

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 2)

Bài 1: Thực hiện các phép tính:

a) -7x²(3x - 4y)

b) (x - 3)(5x - 4)

c) (2x - 1)²

d) (x + 3)(x - 3)

Bài 2: Phân tích đa thức thành nhân tử:

a) 2x³ - 3x² b) x² + 5xy + x + 5y

c) x² - 36 + 4xy + 4y²

Bài 3: Tìm, biết: x² - 5x + 6 = 0

Bài 4: Có 10 túi đựng tiền vàng hình dạng giống hệt nhau. Trong đó, có một túi đựng tiền giả. Những đồng tiền giả nhẹ hơn một gam so với đồng tiền thật nặng 10 gam. Bằng một chiếc cân đồng hồ và với chỉ một lần cân, hãy tìm ra túi đựng tiền giả?

Bài 5: Cho ΔABC vuông tại C (AC < BC), gọi I là trung điểm của AB. Kẻ IE ⊥ BC tại E, kẻ IF ⊥ BC tại F.

a. Chứng minh tứ giác CEIF là hình chữ nhật.

b. Gọi H là điểm đối xứng của I qua F. Chứng minh rằng tứ giác CHFE là hình bình hành.

CI cắt BF tại G, O là trung điểm của FI. Chứng minh ba điểm A, O, G thẳng hàng.

Bài 6:

Tìm các số a,b,c ∈ Q biết a² + b² + c² = ab + bc + ac và a + b + c = 2019.

Đáp án và Hướng dẫn làm bài

Bài 1:

-7x²(3x - 4y)

= -7x².3x + 7x².4y

= -21x³ + 28x²y

(x - 3)(5x - 4)

= x.5x - x.4 - 3.5x + 3.4

= 5x² - 4x - 15x + 12

= 5x² - 19x + 12

(2x - 1)² = 4x² - 4x + 1

(x + 3)(x - 3) = x² - 3² = x² - 9

Bài 2:

a) 2x³ - 3x² = x²(2x - 3)

x² + 5xy + x + 5y

= x(x + 5y) + (x + 5y)

= (x + 1)(x + 5y)

x² - 36 + 4xy + 4y²

= (x² + 4xy + 4y²) - 36

= (x + 2y)² - 6²

= (x + 2y - 6)(x + 2y + 6)

Bài 3:

x² - 5x + 6 = 0

x² - 2x - 3x + 6 = 0

(x² - 2x) - (3x - 6) = 0

(x - 3)(x - 2 = 0)

Trường hợp 1: x - 3 = 0 ⇒ x = 3

Trường hợp 2: x - 2 = 0 ⇒ x = 2

Vậy x ∈ {2, 3}

Bài 4:

Đánh số 10 ví theo thứ tự 1, 2, 3, ..., 10.

Lấy từ ví 1 - 1 đồng

Lấy từ ví 2 - 2 đồng

...

Lấy từ ví 10 - 10 đồng

⇒ Ta lấy được tất cả 55 đồng.

Khi đó, 55 đồng này sẽ cân nặng a gam (a > 0)

Giả sử 55 đồng này đều là tiền thật thì chúng có cân nặng là: 10.55 = 550(gam)

Mà tiền giả nhẹ hơn một gam so với tiền thật nên a < 550

Sau khi cân, thực hiện phép tính 550 - a

Nếu 550 - a = 9 thì ví 1 là ví đựng tiền giả.

Nếu 550 - a = 9.2 thì ví 2 là ví đựng tiền giả.

...

Bài 5:

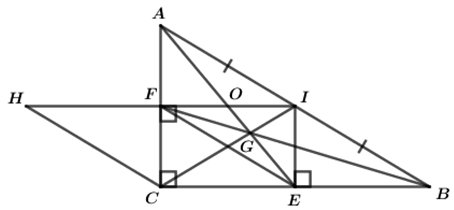
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 1)

Vì ΔABC vuông tại C nên ∠C = 90^o

Ta lại có: IE ⊥ BC tại E và IF ⊥ AC tại F.

⇒ ∠E = 90^o, ∠F = 90^o

Xét tứ giác IFCE ta có: ∠C = ∠E = ∠F = 90^o

⇒ Tứ giác IFCE là hình chữ nhật (dấu hiệu nhận biết).

Vì tứ giác IFCE là hình chữ nhật nên IF = CE và IF // CE.

Vì H là điểm đối xứng của I qua F nên IF = HF và H, F, I thẳng hàng.

⇒ CE = HF và CE // HF

⇒ Tứ giác CHFE là hình bình hàng (dấu hiệu nhận biết hình bình hành)

*) Chứng minh A, G, E thẳng hàng

Giả sử BF ∩ CI = {G}

Xét tam giác ABC ta có:

IA = IB

IF // BC

⇒ F là trung điểm AC.

Tương tự, E là trung điểm của BC

⇒ BF là đường trung tuyến của ΔABC; AE là là đường trung tuyến của ΔABC

Mà CI là là đường trung tuyến của ΔABC và BF ∩ CI = {G}

⇒ G là trọng tâm của ΔABC

⇒ A, G, E thẳng hàng (1)

*) Chứng minh A, O, E thẳng hàng

Ta có:

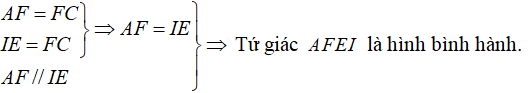
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 1)

Mà O là trung điểm của IF nên O là trung điểm của AE.

⇒ A, O, E thẳng hàng (2)

Từ (1) và (2) suy ra A, O, G thẳng hàng.

Bài 6:

Theo giả thiết, ta có:

a² + b² + c² = ab + bc + ac

2(a² + b² + c²) = 2(ab + bc + ac)

2a² + 2b² + 2c² = 2ab + 2bc + 2ac

2a² + 2b² + 2c² - 2ab - 2bc - 2ac = 0

a² -2ab + b² + a² - 2ac + c² + b² - 2bc + c² = 0

(a - b)² + (a - c)² + (b - c)² = 0

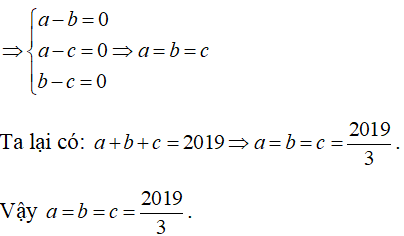
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 1)

Đề thi Toán lớp 8 Giữa kì 1 năm 2021 - 2022 có đáp án (4 Đề)

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 3

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 3)

Câu 1: Phân tích đa thức thành nhân tử:

a. 2x² - 3x - 2 b. 4x(x - 2) + 3(2 - x)

c. 27x³ + 8 d. x² + 2x - y² + 1

Câu 2 (2 điểm): Tìm giá trị của x, biết:

a. 9x² + 6x - 3 = 0 b. x(x - 2)(x + 2) - (x + 2)(x² - 2x + 4) = 4

Câu 3 (2 điểm): Rút gọn và tính giá trị biểu thức:

a. A = x(x + y) - 5(x + y) với x = 1, y = 2

b. B = 3x(x² - 3) + x²(4 - 3x) - 4x² + 1 tại x = 1/9

Câu 4:

Cho hình thang vuông ABCD (∠A = ∠D = 90^o) và CD = 2AB. Kẻ DH vuông góc với AC (H ∈ AC). Gọi M là trung điểm của HC, N là trung điểm của DH. Chứng minh rằng:

a. MN ⊥ AD

b. ABMN là hình bình hành.

c. ∠BMD = 90^o

Câu 5:

1) Cho biểu thức: A = (2x - 3)² - (x + 1)(x + 5) + 2

Rút gọn và tìm giá trị nhỏ nhất của A.

2) Cho B = n² - 27n² + 121. Tìm số tự nhiên n để B là số nguyên.

Đáp án và Hướng dẫn làm bài

Câu 1:

2x² - 3x - 2 = 2x² - 4x + x - 2 = (2x² - 4x) + (x - 2)

= 2x(x - 2) + (x - 2) = (x - 2)(2x + 1)

4x(x - 2) + 3(2 - x) = 4x(x - 2) - (x - 2) = (x - 2)(4x - 1)

27x³ + 8 = (3x)³ + 2³ = (3x + 2)[(3x)² - 2.3x + 2²] = (3x + 2)(9x² - 6x + 2)

x² + 2x - y² + 1 = (x² + 2x + 1) - y² = (x + 1)² - y²

= (x + 1 - y)(x + 1 + y)

Câu 2:

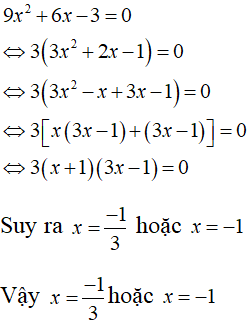
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 3)

x(x - 2)(x + 2) - (x + 2)(x² - 2x + 4) = 4

⇔ x(x² - 4) - (x³ + 8) = 4

⇔ x³ - 4x - x³ - 8 - 4 = 0

⇔ -4x = 12

⇔ x = -3

Suy ra x = -3

Vậy x = -3

Câu 3:

A = x(x + y) - 5(x + y) = (x + y)(x - 5) (*)

Thay x = 1, y = 2 vào biểu thức (*) ta có:

A = (1 + 2)(1 - 5) = 3.(-4) = -12

Vậy với x = 1, y = 2 thì A = -12

b. (1 điểm)

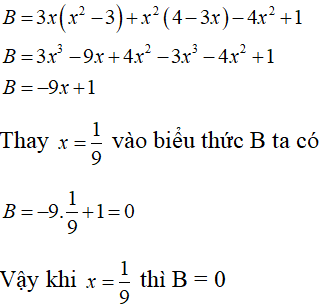
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 3)

Câu 4:

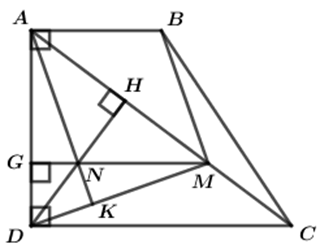
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 3)

a. Vì ABCD là hình thang vuông nên ∠A = ∠D = 90^o

⇒ AD ⊥ DC tại D (1)

Xét tam giác HDC ta có:

NH = ND (giả thiết)

MH = Mc (giả thiết)

⇒ NM là đường trung bình của tam giác HDC

⇒ NM // DC (2)

Từ (1) và (2) suy ra MN ⊥ AD tại G (từ vuông góc đến song song)

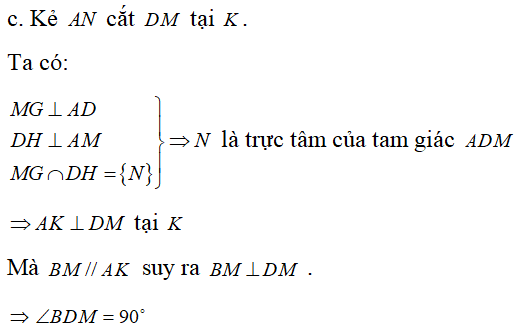
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 3)

Câu 5:

1) A = (2x - 3)² - (x + 1)(x + 5) + 2

= 4x² - 12x + 9 - x² - 6x - 5 + 2 = 3x² - 18x + 6 = 3(x² - 6x + 2)

= 3[(x - 3)² - 7] ≥ 3.(-7) = -21

Dấu "=" xảy ra khi x - 3 = 0 ⇔ x = 3. Vậy MinA = -21 ⇔ x = 3

2) B = n⁴ - 27n² + 121 = n⁴ + 22n² + 121 - 49n²

= (n² + 11)² - (7n)² = (n² + 7n + 11)(n² - 7n + 11)

Vì n ∈ N nên n² -7n + 11 là số tự nhiên lớn hơn 1

Điều kiện cần để B là số nguyên tố là:

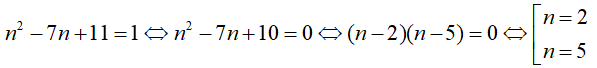
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 3)

- Với n = 2 thì B = 29 (là số nguyên tố)

- Với n = 5 thì B = 71 (là số nguyên tố)

Vậy n ∈ {2, 5} là các giá trị cần tìm.

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 4

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 4)

PHẦN I: TRẮC NGHIỆM (2 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng trong mỗi câu sau vào bài làm.

Câu 1: Kết quả phép tính x(x - y) + y(x + y) tại x = -3 và y = 4 là:

A. 1 B. 7 C. -25

Câu 2: Khai triển biểu thức (x - 2y)³ ta được kết quả là:

A. x³ - 8y³

B. x³ - 2y³

C. x³ - 6x²y + 6xy² - 2y³

D. x³ - 6x²y + 12xy² - 8y³

Câu 3: Giá trị biểu thức 2009² - 2018.2009 + 1009² có bao nhiêu chữ số 0 ?

A. 6

B. 2

C. 4

Câu 4: Đa thức 4x² - 12x + 9 phân tích thành nhân tử là:

A. (2x - 3)²

B. 2x + 3

C. 4x - 9

Câu 5: Hình nào sau đây là tứ giác có hai đường chéo bằng nhau?

A. Hình thang

B. Hình thang cân

C. Hình thang vuông

D. Hình bình hành

Câu 6: Cho tam giác ABC có cạnh BC = 8cm và D, E, M, N lần lượt là trung điểm của AB, AC, BD và CE (như hình vẽ). Khi đó, độ dài của MN là

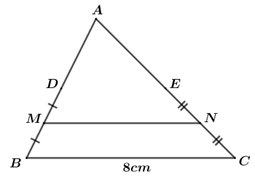
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

A. 7cm B. 5cm C. 6cm D. 4cm

Câu 7: Cho hình bình hành ABCD có ∠A = 60^o. Khi đó, hệ thức nào sau đây là không đúng?

Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

Câu 8: Hình chữ nhật có độ dài cạnh 5cm và 12cm thì khoảng cách từ giao điểm hai đường chéo đến mỗi đỉnh là

A. 17cm

B. 8,5cm

C. 6,5cm

D. 13cm

PHẦN II: TỰ LUẬN (8 điểm)

Câu 1 (VD) (2,25 điểm)

Rút gọn các biểu thức sau:

a. 2x(3x + 2) - 3x(2x + 3)

b. (x + 2)³ + (x - 3)² - x²(x + 5)

c. (3x³ - 4x² + 6x) : 3x

Câu 2 (VD) (0,75 điểm)

Phân tích đa thức sau thành nhân tử: 2x³ - 12x² + 18x

Câu 3 (VD) (1,0 điểm)

Tìm x, biết: 3x(x - 5) - x² + 25 = 0

Câu 4 (VD) (3,0 điểm) Cho hình bình hành ABCD (AB > AD). Gọi E và K lần lượt là trung điểm của CD và AB. BD cắt AE, AC, CK lần lượt tại N, O và I. Chứng minh rằng:

a. Tứ giắc AECK là hình bình hành.

b. Ba điểm E, O, K thẳng hàng.

c. DN = NI = IB

d. AE = 3KI

Câu 5 (VDC) (1,0 điểm) Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:

P = x² + 5y² + 4xy + 6x + 16y + 32

Đáp án và Hướng dẫn làm bài

A. PHẦN TRẮC NGHIỆM

Câu 1:

Thay x = -3 và y = -4 vào biểu thức x(x - y) + y(x + y) ta được:

(-3)(-3 - 4) + 4(-3 + 4) = 21 + 4 = 25

Chọn D.

Câu 2:

Ta có:

(x - 2y³ = x³ - 3x².2y + 3x.(2y)² + (2y)³ = x³ - 6x²y + 12xy² - 8y³

Chọn D.

Câu 3:

2009² - 2018.2009 + 1009²

2009² - 2.2009.1009 + 1009²

= (2009 - 1009)²

= 1000²

= 1000000

Vậy giá trị của biểu thức 2009² - 2018.2009 + 1009² có 6 chữ số 0.

Chọn A.

Câu 4:

4x² - 12x + 9 = (2x)² - 2.2x.3 + 3² = (2x - 3)²

Chọn A.

Câu 5:

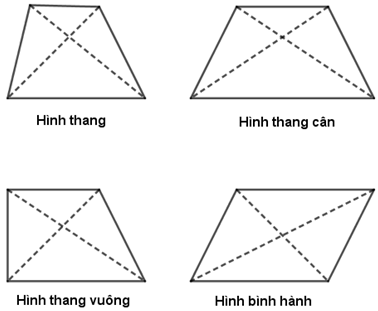
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

Quan sát hình vẽ, và áp dụng tính chất của các hình ta có: Hình thang cân là hình có hai đường chéo bằng nhau.

Chọn B.

Câu 6:

Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

Chọn D.

Câu 7:

Vì ABCD là hình bình hành nên ta có: ∠A = ∠C, ∠B = ∠D và AB // CD, AD // BC

Mà ∠A = 60^o ⇒ ∠C = 60^o

⇒ Đáp án C đúng.

Vì AD // BC mà ∠A và ∠B ở vị trí trong cùng phía nên ta có: ∠A + ∠B = 180^o ⇒ ∠B = 120^o

⇒ ∠B = 2∠C ⇒ Đáp án B đúng.

⇒ ∠A = ∠B/2 ⇒ Đáp án D đúng.

Vì AB // CD mà ∠A và ∠D ở vị trí trong cùng phía nên ta có: ∠A + ∠D = 180^o ⇒ ∠D = 120^o

⇒ Đáp án A sai.

Chọn A.

Câu 8:

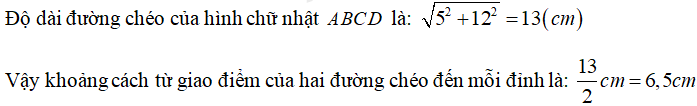
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

Chọn C.

PHẦN II: TỰ LUẬN

Bài 1.

2x(3x + 2) - 3x(2x + 3)

= 2x.3x + 2x.2 - 3x.2x - 3x.3

= 6x² + 4x - 6x² - 9x

= -5x

(x + 2)³ + (x - 3)³ - x²(x + 5)

= (x³ + 6x² + 12x + 8) + (x² - 6x + 9) - (x³ + 5x²)

= x³ + 6x² + 12x + 8 + x² - 6x + 9 - x³ - 5x²

= (x³ - x³) + (6x² + x² - 5x²) + (12x - 6x) + 9

= 2x² + 6x + 9

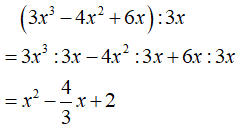
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

Bài 2.

2x³ - 12x² + 18x

= 2x(x² - 6x + 9)

= 2x(x - 3)²

Bài 3.

3x(x - 5) - x² + 25 = 0

3x(x - 5) - (x² + 25) = 0

3x(x - 5) - (x + 5)(x - 5) = 0

(3x - x - 5)(x - 5) = 0

(2x - 5)(x - 5) = 0

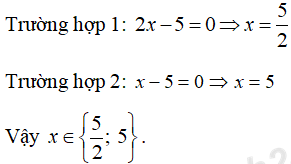
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

Bài 4.

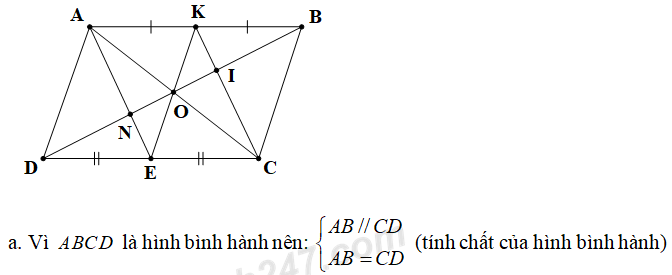
Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

Mà E, K lần lượt là trung điểm của CD và AB nên AK = EC VÀ AK // EC.

⇒ Tứ giác AECK là hình bình hành (dấu hiệu nhận biết)

b. Trong hình bình hành ABCD có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD (tính chất của hình bình hành)

Mà AECK là hình bình hành nên O là trung điểm của EK.

⇒ Ba điểm E, O, K thẳng hàng.

Đề thi Giữa kì 1 Toán lớp 8 năm 2021 - 2022 có đáp án (Đề 2)

Bài 5.

P = x² + 5y² + 4xy + 6x + 16y + 32

⇒ P = x² + (4xy + 6x) + 5y² + 16y + 32

⇒ P = x² + 2x(2y + 3) + (2y + 3)² - (2y + 3)² + 5y² + 16y + 32

⇒ P = [x + (2y + 3)]² - 4y² - 12y - 9 + 5y² + 16y + 32

⇒ P = (x + 2y + 3)² + y² + 4y + 23

⇒ P = (x + 2y + 3)² + (y + 2)² + 19

Vì (x + 2y + 3)² ≥ 0 với mọi x, y ∈ R

(y + 2)² ≥ 0 với mọi y ∈ R

⇒ P = (x + 2y + 3)² + (y + 2)² + 19 ≥ 19 với mọi x, y ∈ R

Dấu "=" xảy ra khi và chỉ khi x + 2y + 3 = 0 và y + 2 =0

Suy ra, x = 1 và y = -2

Vậy P đạt giá trị nhỏ nhất bằng 19 tại x = 1 và y = -2.

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 5

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 5)

I. TRẮC NGHIỆM

Câu 1 Tích của đơn thức: ${x^2}$ và đa thức $5{x^3} - x - 1$ là

A. $5{x^5} - {x^3} - 1$

B. $- 5{x^5} + {x^3} + {x^2}$

C. $5{x^5} + {x^3} + {x^2}$

D. $5{x^5} - x - 1$

Câu 2: Phân tích đa thức thành nhân tử: ${x^2} - 8x$ là:

A. 8-x

B. $x\left( {x - 8} \right)$

C. $x\left( {8 - x} \right)$

D. $- x\left( {x - 8} \right)$

Câu 3: Cho tứ giác ABCD biết $\widehat A = {60^ \circ }$ , $\widehat A = {50^ \circ }$ , $\widehat D = {120^ \circ }$ , khi đó số đo

A. 130

B. 65

C. 170

D. 50

Câu 4: Tìm giá trị nhỏ nhất của biểu thức $A = {x^2} + 4x + 6$ là

A. 6

B. 2

C. 1

D. -2

Câu 5: Cho tam giác ABC có DE là đường trung bình của tam giác ABC. Khẳng định nào sau đây là đúng?

A. $DE = BC$

B. $DE = \frac{1}{3}BC$

C. $DE = \frac{1}{2}BC$

D. $DE = 2BC$

II. TỰ LUẬN

Câu 1:

a) Tìm x biết: $x\left( {x - 2} \right) + \left( {2 - x} \right) = 0$

b) Tính giá trị của biểu thức tại $\left( {x - 4} \right)\left( {x + 4} \right)$ tại $x = 1$

Câu 2: Thực hiện phép tính:

$a)\,2x\left( {3{x^2} - 4x + 1} \right)$

$b)\,\left( {2x + 1} \right)\left( {3{x^3} - {x^2} + 1} \right)$

$c)\,\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)$

Câu 3: Cho tam giác ABC cân tại A . Gọi P, Q lần lượt là trung điểm của AB, AC

a) Tính PQ biết $BC = 8cm$

b) Chứng minh tứ giác PQCB là hình thang cân

c) Kẻ PI vuông góc với BQ tại I $\left( {I \in BQ} \right)$ và CJ vuông góc với BQ tại J $\left( {J \in BQ} \right)$ . Chứng minh rằng: $CJ = 2PI$

Câu 4: Tìm GTLN của biểu thức: $A = 6 - {x^2} - 3x$

Đáp án Đề thi Toán giữa kì 1 lớp 8

1. Đáp án trắc nghiệm

1. A

2. B

3. A

4. B

5. C

2. Đáp án tự luận

Câu 1:

$\begin{array}{l} 1)\,\,\,\,\,x\left( {x - 2} \right) + \left( {2 - x} \right) = 0\\ \,\,\,\,\,\,\,\, \Leftrightarrow x\left( {x - 2} \right) - \left( {x - 2} \right) = 0\\ \,\,\,\,\,\,\, \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) = 0\\ \,\,\,\,\,\,\, \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x - 1 = 0}\\ {x - 2 = 0} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1}\\ {x = 2} \end{array}} \right. \end{array}$

Vậy $x = 1$ hoặc $x = 2$

$2)\,\,\,\left( {x - 4} \right)\left( {x + 4} \right) = {x^2} - 16$ .Với $x = 1$ thì ${x^2} - 16 = {1^2} - 16 = - 15$

Câu 2:

$\begin{array}{l} a)\,2x\left( {3{x^2} - 4x + 1} \right) = 2x.3{x^2} - 2x.4x + 2x.1\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 6{x^3} - 8{x^2} + 2x \end{array}$

$\begin{array}{l} b)\,\left( {2x + 1} \right)\left( {3{x^3} - {x^2} + 1} \right) = 2x.3{x^3} - 2x.{x^2} + 2x.1 + 1.3{x^3} + 1.\left( { - {x^2}} \right) + 1.1\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 6{x^4} - 2{x^3} + 2x + 3{x^3} - {x^2} + 1\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 6{x^4} + {x^3} + 2x - {x^2} + 1 \end{array}$

$c)\,\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right) = {x^3} - {y^3}$

Câu 3:

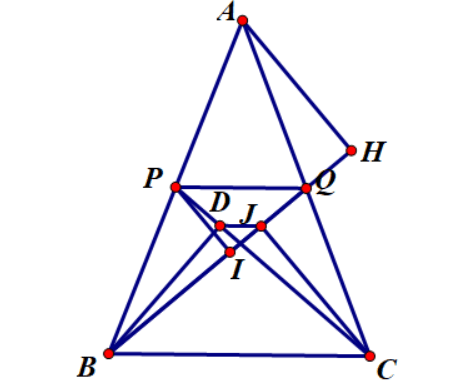
Đề thi giữa kì 1 môn Toán lớp 8 năm học 2022-2023 - Đề 4

a) Tính PQ

Xét tam giác ABC có: $\left\{ {\begin{array}{*{20}{c}} {AM = MB}\\ {AN = NC} \end{array}} \right.\,\,\,\,\,\,\left( {gt} \right)$

PQ là đường trung bình của tam giác ABC

$\Rightarrow MN = \frac{1}{2}BC = \frac{1}{2}.8 = 4\,\,\,\left( {cm} \right)$

b) Chứng minh PQBC là hình thang cân:

Vì PQ là đường trung bình của tam giác $\Rightarrow PQ//BC$ $\Rightarrow$ PQBC là hình thang

Mà $\widehat {PBC} = \widehat {QCB}$ ( $\Delta ABC$ cân tại A) PQBC là hình thang cân

c) Kẻ AH vuông góc với BQ:

Xét $\Delta ABH$ có $\left\{ \begin{array}{l} BP = AP\\ PI//AH\left( { \bot BQ} \right) \end{array} \right.$ $\Rightarrow$ PI là đường trung bình của tam giác

$\Rightarrow PI = \frac{1}{2}AH$

Xét $\Delta AQH$ và $\Delta CQJ$ có: $\left\{ \begin{array}{l} AQ = QC\\ \widehat {AQH} = \widehat {JQC}\left( {d\,d} \right)\\ \widehat {AHQ} = \widehat {QJC} = {90^ \circ } \end{array} \right.$ $\Rightarrow \Delta AQH = \Delta CQJ \Rightarrow AH = CJ \Rightarrow PI = \frac{1}{2}CJ$

Câu 4:

$A = 6 - {x^2} - 3x = - {x^2} - 3x + 6 = - \left( {{x^2} + 3x - 6} \right)$

$= - \left[ {\left( {{x^2} + 2.x.\frac{3}{2} + {{\left( {\frac{3}{2}} \right)}^2} - \frac{{33}}{6}} \right)} \right] = - \left[ {{{\left( {x - \frac{3}{2}} \right)}^2} - \frac{{33}}{6}} \right]$

Nhận thấy:

$\begin{array}{l} {\left( {x - \frac{3}{2}} \right)^2} \ge 0\\ \Rightarrow {\left( {x - \frac{3}{2}} \right)^2} - \frac{{33}}{6} \ge - \frac{{33}}{6}\\ \Rightarrow - \left[ {{{\left( {x - \frac{3}{2}} \right)}^2} - \frac{{33}}{6}} \right] \le \frac{{33}}{6} \end{array}$

Dấu bằng xảy ra khi:

$\begin{array}{l}{\left( {x - \dfrac{3}{2}} \right)^2} = 0\\ \Leftrightarrow x - \dfrac{3}{2} = 0\\ \Leftrightarrow x = \dfrac{3}{2}\end{array}$

Vậy GTLN của $A = \frac{{33}}{6}$ khi $x = \frac{3}{2}$

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 6

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 6)

Câu 1 (2 điểm) Phân tích đa thức thành nhân tử

a. ${x^2}y + x{y^2} - 5x - 5y$	b. ${x^2} - x - 12$
c. $3{x^2} - 16x + 5$	d. ${x^3} - 4{x^2} - 9x + 36$

Câu 2 (2 điểm) Tìm giá trị của x, biết:

a. $x\left( {4x + 3} \right) - \left( {1 + 3x} \right) = 0$

b. ${x^3} - 16x = 0$

c. $19 + x{\left( {x - 2} \right)^2} = \left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right)$

Câu 3 (2 điểm) Chứng minh biểu thức sau không phụ thuộc vào x

a. $A = {\left( {3x + 5} \right)^2} - {\left( {3x - 5} \right)^2} - 60\left( {x + \frac{1}{3}} \right) + 20$

b. $B = {\left( {2x + y} \right)^3} - 2x\left( {4{x^2} + 3{y^2}} \right) + 4x\left( { - 3xy} \right) - {y^3}$

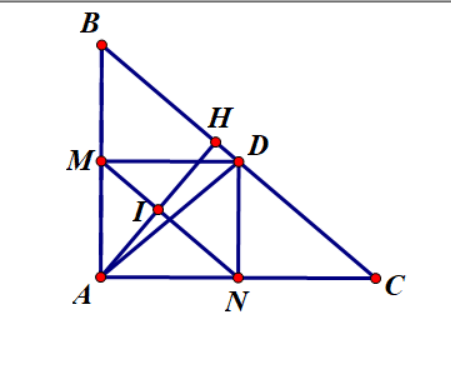
Câu 4 (2 điểm) Cho hình chữ nhật ABCD, AC giao với BD tại O. Chọn một điểm E bất kì nằm giữa hai điểm B và O, F là điểm đối xứng với A qua E. Lấy điểm I nằm trên CF sao cho CI = IF. Gọi H và K lần lượt là hình chiếu của F trên các đường thẳng BC và CD.

a. Tứ giác OECI là hình gì? Giải thích tại sao

b. Chứng minh tứ giác CHFK là hình chữ nhật.

c. Chứng minh bốn điểm K, I, H, E thẳng hàng.

Câu 5 (0,5 điểm) Cho x. y, z thỏa mãn:

${x^{2014}} + {y^{2014}} + {x^{2014}} = {x^{1007}}{y^{1007}} + {y^{1007}}.{z^{1007}} + {z^{1007}}.{x^{1007}}$

Tính giá trị của biểu thức

$P = {\left( {x - y} \right)^{2014}} + {\left( {y - z} \right)^{2014}} + {\left( {x - z} \right)^{2014}}$

Đáp án Đề thi Toán giữa kì 1 lớp 8

Câu 1:

a. Ta có:

$\begin{matrix} {x^2}y + x{y^2} - 5x - 5y \hfill \\ = \left( {{x^2}y + x{y^2}} \right) + \left( { - 5x - 5y} \right) \hfill \\ = xy\left( {x + y} \right) - 5\left( {x + y} \right) \hfill \\ = \left( {xy - 5} \right)\left( {x + y} \right) \hfill \\ \end{matrix}$

b. Ta có:

$\begin{matrix} {x^2} - x - 12 \hfill \\ = {x^2} - 2.\dfrac{1}{2}x + \dfrac{1}{4} - \dfrac{1}{4} - 12 \hfill \\ = {\left( {x - \dfrac{1}{2}} \right)^2} - \dfrac{{49}}{4} = {\left( {x - \dfrac{1}{2}} \right)^2} - {\left( {\dfrac{7}{2}} \right)^2} \hfill \\ = \left( {x - \dfrac{1}{2} + \dfrac{7}{2}} \right)\left( {x - \dfrac{1}{2} - \dfrac{7}{2}} \right) \hfill \\ = = \left( {x + 3} \right)\left( {x - 4} \right) \hfill \\ \end{matrix}$

c. Ta có:

$\begin{matrix} 3{x^2} - 16x + 5 \hfill \\ = 3{x^2} - x - 15x + 5 \hfill \\ = \left( {3{x^2} - x} \right) + \left( { - 15x + 5} \right) \hfill \\ = x\left( {3x - 1} \right) - 15\left( {x - 1} \right) \hfill \\ = \left( {x - 15} \right)\left( {3x - 1} \right) \hfill \\ \end{matrix}$

d. Ta có:

$\begin{matrix} {x^3} - 4{x^2} - 9x + 36 \hfill \\ = \left( {{x^3} - 4{x^2}} \right) + \left( { - 9x + 36} \right) \hfill \\ = {x^2}\left( {x - 4} \right) - 9\left( {x - 4} \right) \hfill \\ = \left( {{x^2} - 9} \right)\left( {x - 4} \right) \hfill \\ = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 4} \right) \hfill \\ \end{matrix}$

Bài 2:

$\begin{matrix} x\left( {4x + 3} \right) - \left( {1 + 3x} \right) = 0 \hfill \\ \Leftrightarrow 4{x^2} + 3x - 1 - 3x = 0 \hfill \\ \Leftrightarrow 4{x^2} - 1 = 0 \hfill \\ \Leftrightarrow {\left( {2x} \right)^2} - {1^2} = 0 \hfill \\ \Leftrightarrow \left( {2x - 1} \right)\left( {2x + 1} \right) = 0 \hfill \\ \end{matrix}$

Suy ra $x = \frac{1}{2}$ hoặc $x = - \frac{1}{2}$

$\begin{matrix} {x^3} - 16x = 0 \hfill \\ \Leftrightarrow x\left( {{x^2} - 16} \right) = 0 \hfill \\ \Leftrightarrow x\left( {x - 4} \right)\left( {x + 4} \right) = 0 \hfill \\ \end{matrix}$

Suy ra x = 0 hoặc x = 4 hoặc x = -4

c. $19 + x{\left( {x - 2} \right)^2} = \left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right)$

$\begin{matrix} \Leftrightarrow 19 + x\left( {{x^2} - 4x + 4} \right) = {x^3} + {3^3} \hfill \\ \Leftrightarrow 19 + {x^3} - 4{x^2} + 4x - {x^3} - 27 = 0 \hfill \\ \Leftrightarrow - 4{x^2} + 4x - 8 = 0 \hfill \\ \Leftrightarrow - 4\left( {{x^2} - x + 2} \right) = 0 \hfill \\ \Leftrightarrow - 4\left[ {{{\left( {x - \dfrac{1}{2}} \right)}^2} + \dfrac{7}{4}} \right] < 0\forall x \hfill \\ \end{matrix}$

Vậy không có giá trị nào của x thỏa mãn biểu thức.

Câu 3:

a. $A = {\left( {3x + 5} \right)^2} - {\left( {3x - 5} \right)^2} - 60\left( {x + \frac{1}{3}} \right) + 20$

$\begin{matrix} A = 9{x^2} + 30x + 25 - 9{x^2} + 30x - 25 - 60x - 20 + 20 \hfill \\ A = 0 \hfill \\ \end{matrix}$

Vậy biểu thức A không phụ thuộc vào biến x

b. $B = {\left( {2x + y} \right)^3} - 2x\left( {4{x^2} + 3{y^2}} \right) + 4x\left( { - 3xy} \right) - {y^3}$

$\begin{matrix} B = {\left( {2x} \right)^3} + 3.{\left( {2x} \right)^2}.y + 3.\left( {2x} \right).{y^2} + {y^3} - 8{x^3} - 6x{y^2} - 12{x^2}y - {y^3} \hfill \\ B = 8{x^3} + 12{x^2}y + 6x{y^2} + {y^3} - 8{x^3} - 6x{y^2} - 12{x^2}y - {y^3} \hfill \\ B = 0 \hfill \\ \end{matrix}$

Vậy biểu thức B không phụ thuộc vào x

Câu 4:

Hình vẽ minh họa:

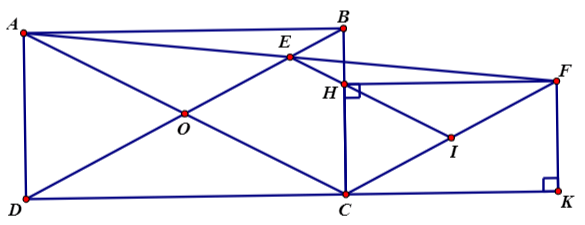
Đề thi giữa kì 1 Toán 8 năm học 2022 - 2023 Đề số 1

Chứng minh OE là đường trung bình của tam giác ACF => OE // CF, OE = ½ CF

=> OE // CI (1)

Mà IC = IF

=> OE = CI (2)

Từ (1) và (2) => OEIC là hình bình hành

Tứ giác ABCD là hình chữ nhật

$\Rightarrow \widehat {BCD} = {90^0} \Rightarrow \widehat {BCK} = {90^0}$

Chứng minh được tứ giác CHFK có ba góc vuông nên là hình chữ nhật

Ta có ABCD là hình chữ nhật => Tam giác COB cân tại O

$\Rightarrow \widehat {OBC} = \widehat {BCO}$

Do OE // CF

$\begin{matrix} \Rightarrow \widehat {OBC} = \widehat {BCF}\left( {slt} \right) \hfill \\ \Rightarrow \widehat {OCF} = 2\widehat {BCF} = 2\widehat {HCF} = {180^0} - 2\widehat {HCF}\left( * \right) \hfill \\ \end{matrix}$

Tam giác HIF cân tại I $\Rightarrow \widehat {HIF} = {180^0} - 2\widehat {HCF}\left( {**} \right)$

Từ (*) và (**) $\Rightarrow \widehat {OCF} = \widehat {HIF} \Rightarrow OC//HI$

Kết hợp với OC // EI ta có ba điểm E, H, I thẳng hàng

Lập luận ba điểm H, I, K thẳng hàng

=> Bốn điểm K, I, H, E thẳng hàng

Câu 5:

$\begin{matrix} {x^{2014}} + {y^{2014}} + {x^{2014}} = {x^{1007}}{y^{1007}} + {y^{1007}}.{z^{1007}} + {z^{1007}}.{x^{1007}} \hfill \\ \Rightarrow 2\left( {{x^{2014}} + {y^{2014}} + {x^{2014}}} \right) = 2\left( {{x^{1007}}{y^{1007}} + {y^{1007}}.{z^{1007}} + {z^{1007}}.{x^{1007}}} \right) \hfill \\ \Rightarrow {\left( {x - y} \right)^{2014}} + {\left( {y - z} \right)^{2014}} + {\left( {x - z} \right)^{2014}} = 0 \hfill \\ \Rightarrow P = 0 \Rightarrow x = y = z \hfill \\ \end{matrix}$

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 7

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 7)

Câu 1 (2 điểm) Thực hiện phép tính:

a. $2x\left( {x - 3} \right) + \left( {x - 2} \right)\left( {5 - 2x} \right)$

b. $\left( {20{x^2}{y^2} - 5{x^2}y + 15{x^2}{y^3}} \right):5{x^2}y$

Câu 2 (2 điểm) Phân tích đa thức thành nhân tử

a. $5{x^2}\left( {2{x^2} - 3x + 1} \right)$	b. $\left( {x - 2y} \right)\left( {{x^2} - xy - 6{y^2}} \right)$
c. $4{x^4} + 81$	d. $8{x^4} - 15{x^2} + 7$

Câu 3 (2 điểm) Tìm giá trị của x, biết:

a. $x\left( {x - 1} \right) - x\left( {x - 3} \right) = 0$	b. ${x^2} - 6x + 8 = 0$
c. $2{x^2} - 2x + \frac{1}{2} = 0$

Câu 4 (1 điểm) Một mặt sàn hình chữ nhật rộng 8m, dài 10m. Người ta dự định lát gạch hoa trên toàn bộ mặt sân bằng những viên gạch vuông cạnh 40cm. Mỗi viên gạch có giá 20 000.

a. Tính diện tích mặt sân.

b. Số tiền để mua số gạch để lát hết mặt sân.

Câu 5 (2 điểm) Cho hình bình hành ABCD có cạnh AD = m và AB = 2m. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi P là giao điểm của AN với DM, Q là giao điểm của CM với BN.

Chứng minh:

a. Tam giác ADN cân và AN là phân giác của góc $\widehat {DAB}$ .

b. MD // NB.

c. Tứ giác PMQN là hình chữ nhật.

Câu 6 (1 điểm) Chứng minh rằng với mọi số nguyên a chẵn lớn hơn 4 thì

${a^4} - 4{a^3} - 4{a^2} + 16a \vdots 384$

Đáp án Đề thi Toán giữa kì 1 lớp 8

Câu 1:

a. $2x\left( {x - 3} \right) + \left( {x - 2} \right)\left( {5 - 2x} \right) = 2{x^2} - 6x + 5x - 4{x^2} - 10 + 4x = - 2{x^2} + 3x - 10$

b. $\left( {20{x^2}{y^2} - 5{x^2}y + 15{x^2}{y^3}} \right):5{x^2}y = 4y - 1 + 3{y^2}$

Câu 2:

a. $5{x^2}\left( {2{x^2} - 3x + 1} \right) = 5{x^2}.\left( {2{x^2} - 2x - x + 1} \right)$

$= 5{x^2}\left[ {2x\left( {x - 1} \right) - \left( {x - 1} \right)} \right] = 5{x^2}\left( {x - 1} \right)\left( {2x - 1} \right)$

$\begin{matrix} \left( {x - 2y} \right)\left( {{x^2} - xy - 6{y^2}} \right) = \left( {x - 2y} \right)\left( {{x^2} + 2xy - 3xy - 6{y^2}} \right) \hfill \\ = \left( {x - 2y} \right)\left[ {x\left( {x + 2y} \right) - 3y\left( {x + 2y} \right)} \right] = \left( {x - 2y} \right)\left( {x + 2y} \right)\left( {x - 3y} \right) \hfill \\ \end{matrix}$

c. ${x^4} + 81 = {x^4} + 18{x^2} + 81 - 36{x^2} = {\left( {{x^2} + 9} \right)^2} - {\left( {6x} \right)^2} = \left( {{x^2} + 9 - 6x} \right)\left( {{x^2} + 9 + 6x} \right)$

d. $8{x^4} - 15{x^2} + 7 = 8{x^4} - 8{x^2} - 7{x^2} + 7$

$= 8{x^2}\left( {{x^2} - 1} \right) - 7\left( {{x^2} - 1} \right) = \left( {{x^2} - 1} \right)\left( {8{x^2} - 7} \right)$

Câu 3:

a. x = 0

b. x = 2 hoặc x = 4

c. x = -1/2

Câu 4:

a. Diện tích mặt sàn là: 80m²

b. Diện tích 1 viên gạch là: 0,16m²

Số viên gạch cần dùng để lát hết sân là: 500 viên gạch

Số tiền để mua gạch là: 10 000 000 đồng

Câu 5:

Hình vẽ minh họa:

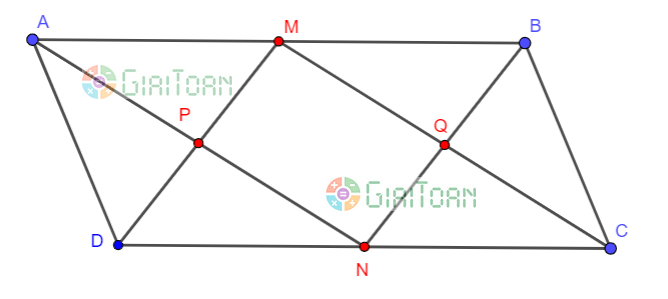
Đề thi giữa kì 1 Toán 8 năm học 2022 - 2023 Đề số 2

a) Ta có AD = DN => Tam giác AND cân tại D

$\widehat {BAN} = \widehat {DAN}$ => AD là phân giác góc DAB

Tứ giác BMDN là hình bình hành

=> DM // NB

Xét tứ giác MPNQ có:

MD // NB (cmt) => MP //NQ

=> MNPQ là hình bình hành

Ta có AN là phân giác hóc DAB => AN là phân giác góc MAD

Do tam giác ADM cân tại A

=> AP ⊥ DN

=> MPNQ là hình chữ nhật

Câu 6:

Ta có:

$\begin{matrix} {a^4} - 4{a^3} - 4{a^2} + 16a \hfill \\ = a\left( {{a^3} - 4{a^2} - 4a + 16} \right) \hfill \\ = a\left[ {{a^2}\left( {a - 4} \right) - 4\left( {a - 4} \right)} \right] \hfill \\ = a\left( {a - 4} \right)\left( {{a^2} - 4} \right) \hfill \\ = a\left( {a - 4} \right)\left( {a - 2} \right)\left( {a + 2} \right) \hfill \\ \end{matrix}$

Vì a là số chẵn lớn hơn 4 nên $\left( {a - 4} \right)\left( {a - 2} \right)a\left( {a + 2} \right)$ là 4 số chẵn liên tiếp, có một số chia hết cho 2, cho 4, cho 6, cho 8

=> Biểu thức chia hết cho 384

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 8

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 8)

Câu 1 (2 điểm) 1. Rút gọn biểu thức: ${\left( {2x + 1} \right)^2} - 2\left( {2x - 1} \right)\left( {2x + 1} \right) + {\left( {2x - 1} \right)^2}$

2. Thực hiện phép chia:

$\left( {{a^5} - 3{a^4} - {a^2} + 5{a^3} + 3a - 5} \right):\left( { - 3a + {a^2} + 5} \right)$

3. Chứng minh biểu thức sau không phụ thuộc vào biến:

$6\left( {3x - 4} \right) - 5\left( {x - 3} \right) - 19x + 3\left( {2x - 1} \right)$

Câu 2 (2 điểm) Phân tích đa thức thành nhân tử

a. ${x^2} - 6x - {y^2} + 9$	b. $2x - 8xy + 8x{y^2}$
c. ${x^4} + 2{x^2}y + {y^2} - 9$

Câu 3 (2 điểm) Tìm giá trị của x, biết:

a. ${\left( {x + 3} \right)^2} - 4x - 17 = \left( {x + 2} \right)\left( {x - 2} \right)$

b. $\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) - 1 = 0$

Câu 4 (1 điểm)

1. Tìm m để đa thức $2{x^3} - 3{x^2} + x + m$ chia hết cho đa thức x + 1.

2. Cho hai số không âm a và b thỏa mãn ${a^2} + {b^2} = a + b$ . Tính giá trị lớn nhất của biểu thức:

$A = \frac{a}{{a + 1}} + \frac{b}{{b + 1}}$

Câu 5 (3 điểm) Cho hình bình hành ABCD có AD = 2AB. Từ C kẻ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M kẻ MF vuông góc với CE, MF vuông góc với BC tại N.

a. Tứ giác MNCD là hình gì?

b. Tam giác CME là tam giác gì?

c. Chứng minh $\widehat {BAD} = 2\widehat {AEM}$

Đáp án Đề thi Toán giữa kì 1 lớp 8

Câu 1 (2 điểm)

1. ${\left( {2x + 1} \right)^2} - 2\left( {2x - 1} \right)\left( {2x + 1} \right) + {\left( {2x - 1} \right)^2}$

$\begin{matrix} = {\left[ {\left( {2x + 1} \right) - \left( {2x - 1} \right)} \right]^2} \hfill \\ = {\left[ {2x + 1 - 2x + 1} \right]^2} \hfill \\ = {2^2} = 4 \hfill \\ \end{matrix}$

$\begin{matrix} \left( {{a^5} - 3{a^4} + 5{a^3}} \right) + \left( { - {a^2} + 3a - 5} \right) \hfill \\ = {a^3}\left( {{a^2} - 3a + 5} \right) - \left( {{a^2} - 3a + 5} \right) \hfill \\ = \left( {{a^2} - 1} \right)\left( {{a^2} - 3a + 5} \right) \hfill \\ \Rightarrow \left( {{a^5} - 3{a^4} - {a^2} + 5{a^3} + 3a - 5} \right):\left( { - 3a + {a^2} + 5} \right) = {a^2} - 1 \hfill \\ \end{matrix}$

$\begin{matrix} 6\left( {3x - 4} \right) - 5\left( {x - 3} \right) - 19x + 3\left( {2x - 1} \right) \hfill \\ = 18x - 24 - 5x + 15 - 19x + 6x - 3 \hfill \\ = \left( {18x - 5x - 19x + 6x} \right) + \left( { - 24 + 15 - 3} \right) \hfill \\ = 0x - 12 = - 12 \Rightarrow dpcm \hfill \\ \end{matrix}$

Câu 2 (2 điểm)

a. ${x^2} - 6x - {y^2} + 9 = \left( {{x^2} - 6x + 9} \right) - {y^2} = {\left( {x - 3} \right)^2} - {y^2} = \left( {x - 3 - y} \right)\left( {x - 3 + y} \right)$

b. $2x - 8xy + 8x{y^2} = 2x\left( {1 - 4y + 4{y^2}} \right) = 2x{\left( {1 - 2y} \right)^2}$

$\begin{matrix} {x^4} + 2{x^2}y + {y^2} - 9 \hfill \\ = \left( {{x^4} + 2{x^2}y + {y^2}} \right) - {3^2} \hfill \\ = {\left( {{x^2} + y} \right)^2} - {3^2} \hfill \\ = \left( {{x^2} + y - 3} \right)\left( {{x^2} + y + 3} \right) \hfill \\ \end{matrix}$

Câu 3 (2 điểm)

a) ${\left( {x + 3} \right)^2} - 4x - 17 = \left( {x + 2} \right)\left( {x - 2} \right)$

$\begin{matrix} \Rightarrow {x^2} + 6x + 9 - 4x - 17 = {x^2} - 4 \hfill \\ \Rightarrow {x^2} + 6x + 9 - 4x - 17 - {x^2} + 4 = 0 \hfill \\ \Rightarrow 2x - 4 = 0 \hfill \\ \Rightarrow x = 2 \hfill \\ \end{matrix}$

Vậy x = 2

b) $\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) - 1 = 0$

$\begin{matrix} \Rightarrow {x^3} - 27 - {x^3} + 4x - 1 = 0 \hfill \\ \Rightarrow 4x - 28 = 0 \hfill \\ \Rightarrow x = 7 \hfill \\ \end{matrix}$

Vậy x = 7

Câu 4:

1) $\left( {2{x^3} - 3{x^2} + x + m} \right):\left( {x + 1} \right) = 2{x^2} - 5x + 6$ dư (m – 6)

Để phép chia là phép chia hết thì m – 6 = 0

=> m = 6

2) $\left\{ {\begin{array}{*{20}{c}} {{a^2} + 1 \geqslant 2a} \\ {{b^2} + 1 \geqslant 2b} \end{array} \Rightarrow {a^2} + {b^2} + 2 \geqslant 2a + 2b \Rightarrow a + b \leqslant 2} \right.$

Chứng minh được với hai số dương m, n bất kì thì $\frac{1}{m} + \frac{1}{n} \geqslant \frac{4}{{m + n}}$

$A = \frac{a}{{a + 1}} + \frac{b}{{b + 1}} = 2 - \left( {\frac{1}{{a + 1}} + \frac{1}{{b + 1}}} \right) \leqslant 2 - \frac{4}{{a + 1 + b + a}} \leqslant 1$

Do đó:

Vậy GTLN của A là 1, đạt được khi a = b = 1

Câu 5:

Hình vẽ minh họa:

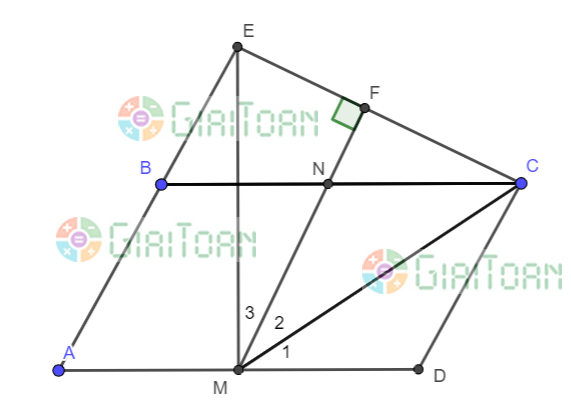
Đề thi giữa kì 1 Toán 8 năm học 2021 - 2022 Đề số 3

a) Ta có: $\left\{ {\begin{array}{*{20}{c}} {CE \bot AB} \\ {MF \bot EC} \end{array} \Rightarrow MF//AB//CD} \right.$ => MNCD là hình bình hành

Ta lại có: $MD = \frac{1}{2}AD = AB = CD$ => MNCD là hình thoi

b) Từ chứng minh trên ta có:

$CN = CD = \frac{1}{2}BC;NF//BE \Rightarrow EF = FC$

Tam giác CME có FM vừa là đường cao vừa là đường trung tuyến là tam giác CME là tam giác cân tại M.

c) Ta có:

$\left\{ {\begin{array}{*{20}{c}} {\widehat {BAD} = \widehat {NMD}\left( {dv} \right)} \\ {\widehat {NMD} = \widehat {{M_1}} + \widehat {{M_2}} = 2\widehat {{M_3}}} \\ {\widehat {{M_3}} = \widehat {AEM}\left( {slt} \right)} \end{array}} \right. \Rightarrow \widehat {BAD} = 2\widehat {AEM}$

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 9

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 9)

Bài 1: (3,0 điểm) Rút gọn các biểu thức sau:

1/ (x – 3)(x + 3) – (x – 3)²

2/ (x – 2)(x² + 2x + 4) – x³ + 5

Bài 2: (3,0 điểm) Phân tích các đa thức sau thành nhân tử

1/ x²– y² - 5x + 5y

2/ 5x³ – 5x²y – 10x² + 10xy

3/ x² + 5x + 4

Bài 3: (1,0 điểm) Chứng minh rằng biểu thức (5n -2)² – (2n -5)² luôn chia hết cho 21, với mọi giá trị nguyên n.

Bài 4: (3,0 điểm) Cho tam giác ABC có BC = 4cm, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC.

1/ Tính độ dài ED

2/ Chứng minh DE//IK

3/ Chứng minh tứ giác EDKI là hình bình hành.

Đáp án đề kiểm tra giữa kì 1 Toán 8

Bài

Câu

Nội dung

Điểm

Bài 1

(3,0 đ)

1,5 đ

(x – 3)(x + 3) – (x – 3)² =

= x²– 9 – x² + 6x – 9

= 6x – 18

0,75 đ

1,5 đ

(x – 2)(x² + 2x + 4) – x³ + 5 =

= x³ – 8 – x³+ 5

= -3

0,75 đ

Bài 2

(3,0 đ)

1,0 đ

x²– y² - 5x + 5y =

= (x – y)(x + y) – 5(x – y)

= (x – y)(x + y – 5)

0,5 đ

0,5đ

1,0 đ

5x³ – 5x²y – 10x² + 10xy =

= 5x(x² – xy – 2x + 2y)

= 5x[x(x – y) – 2(x – y)]

= 5x(x – y)(x – 2)

0,5 đ

0,25đ

0,25 đ

1,0 đ

x² + 5x + 4 =

= x² + x + 4x + 4

= x(x + 1) + 4(x + 1)

= (x + 1)(x + 4)

0,5 đ

0,25đ

0,25 đ

Bài 3

(1,0 đ)

Ta có:

(5n -2)² – (2n -5)² =

= (5n – 2 – 2n + 5)( 5n – 2 + 2n – 5)

= (3n + 3)(7n – 7)

= 21(n + 1)(n – 1)

Mà 2121 nên 21(n + 1)(n – 1) 21

Vậy (5n -2)² – (2n -5)² 21

0,25 đ

0,25đ

0,25 đ

Bài 4

(3,0 đ)

1,25 đ

*/ Vẽ hình đúng

*/Tam giác ABC có:

EA = EB (Vì CE là trung tuyến)

DA = DC (Vì BD là trung tuyến)

Do đó, ED là đường trung bình của tam giác ABC

$\Rightarrow \mathrm{ED}=\frac{1}{2} \mathrm{BC}$ (1)

$\mathrm{ED} / / \mathrm{BC}$

Vậy ED = 2(cm)

0,25 đ

1,0 đ

Tam giác BGC có:

IB = IG (gt)

KC = KG (gt)

Do đó, IK là đường trung bình của tam giác BGC

$\Rightarrow I K=\frac{1}{2} \mathrm{BC}$
và $\mathrm{IK} / / \mathrm{BC}$ (2)

Từ (1) và (2) suy ra ED // IK

0,25 đ

0,75 đ

Từ (1) và (2) suy ra

$\Rightarrow I K=\mathrm{ED}$

và $\mathrm{IK} / / \mathrm{ED}$

Do đó EDKI là hình bình hành

0,25 đ

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 10

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 10)

A. Phần trắc nghiệm

Câu 1: Với giá trị nào của a thì biểu thức ${x^2} - 2x + a$ viết được dưới dạng bình phương của một tổng

A. a = 1	B. a = 9
C. a = 16	D. a = 6

Câu 2: Tính giá trị của biểu thức ${x^2} - 4x + 4$ tại x = 4

A. 3	B. 4
C. -3	D. – 4

Câu 3: Đơn thức thích hợp để điền vào chỗ trống của …….. – 16 = (3x - 4)(3x+4)

A. $3{x^2}$	B. 6x
C. $9{x^2}$	D. $- 9{x^2}$

Câu 4: Điền vào chỗ trống: ${\left( {x - 2y} \right)^3} = \left( {.......} \right)\left( {{x^2} + 2xy + 4{y^2}} \right)$

A. x + 2y	B. x – 2y
C. –x+2y	D. –x – 2y

Câu 5: Tứ giác ABCD có $\widehat A = {120^ \circ };\widehat B = {60^ \circ };\widehat C = {110^ \circ }$ thì

A. $D = {180^ \circ }$	B. $D = {60^ \circ }$
C. $D = {110^ \circ }$	D. $D = {70^ \circ }$

B. Phần tự luận

Câu 1: Rút gọn biểu thức:

$\begin{array}{l} a)\,\,\,3{x^2}\left( {{x^2} - 5x} \right)\\ b)\,\,{\left( {x - 1} \right)^2} - \left( {x + 2} \right)\left( {x - 2} \right) + 2x\\ c)\,\,{\left( {3x + 1} \right)^2} - 2\left( {3x - 1} \right)\left( {3x + 1} \right) + {\left( {3x - 1} \right)^2} \end{array}$

Câu 2: Phân tích đa thức thành nhân tử:

$\begin{array}{l} a)\,\,6{x^3} - 6x\\ b)\,\,{x^2} + 4x - xy - 4y\\ c)\,{x^2} + 4x - 4{y^2} + 4 \end{array}$

Câu 3: Tìm x biết:

$\begin{array}{l} a)\,\,x\left( {x - 4} \right) - 2{x^2} = 0\\ b)\,\,{x^3} - 8 = 0 \end{array}$

Câu 4: Cho tam giác ABC có D là trung điểm của AC. Qua D kẻ đường thẳng DF // AB và DE // BC

a) Chứng minh BDEF là hình bình hành

b) Gọi K là điểm đối xứng với D qua F. Chứng minh rằng BK // AD

Đáp án Đề thi Toán giữa kì 1 lớp 8

A. Phần trắc nghiệm

1. A

2. B

3. C

4. B

5.D

B. Phần tự luận

Câu 1: Rút gọn biểu thức:

Hướng dẫn giải

$\begin{array}{l} a)\,\,\,3{x^2}\left( {{x^2} - 5x} \right)\\ = 3{x^4} - 15{x^3}\\ b)\,\,{\left( {x - 1} \right)^2} - \left( {x + 2} \right)\left( {x - 2} \right) + 2x\\ = {x^2} - 2x + 1 - {x^2} + 4 + 2x\\ = 5\\ c)\,\,{\left( {3x + 1} \right)^2} - 2\left( {3x - 1} \right)\left( {3x + 1} \right) + {\left( {3x - 1} \right)^2}\\ = {\left( {3x + 1 - 3x + 1} \right)^2}\\ = {2^2} = 4 \end{array}$

Câu 2: Phân tích đa thức thành nhân tử:

$\begin{array}{l} a)\,\,6{x^3} - 6x\\ b)\,\,{x^2} + 4x - xy - 4y\\ c)\,{x^2} + 4x - 4{y^2} + 4 \end{array}$

Hướng dẫn giải

$\begin{array}{l} a)\,\,6{x^3} - 6x\\ = 6x\left( {{x^2} - 1} \right) = 6x\left( {x - 1} \right)\left( {x + 1} \right)\\ b)\,\,{x^2} + 4x - xy - 4y\\ = x\left( {x + 4} \right) - y\left( {x + 4} \right)\\ = \left( {x + 4} \right)\left( {x - y} \right)\\ c)\,{x^2} + 4x - 4{y^2} + 4\\ = \left( {{x^2} + 4x + 4} \right) - 4{y^2}\\ = {\left( {x + 2} \right)^2} - {\left( {2y} \right)^2}\\ = \left( {x + 2 - 2y} \right)\left( {x + 2 + 2y} \right) \end{array}$

Câu 3: Tìm x biết:

$\begin{array}{l} a)\,\,x\left( {x - 4} \right) - 2{x^2} = 0\\ b)\,\,{x^3} - 8 = 0 \end{array}$

Hướng dẫn giải

$\begin{array}{l} a)\,\,x\left( {x - 4} \right) - 2{x^2} + 4x + 9 = 0\\ \Leftrightarrow {x^2} - 4x - 2{x^2} + 4x + 9 = 0\\ \Leftrightarrow - {x^2} + 9 = 0\\ \Leftrightarrow \left( {3 - x} \right)\left( {3 + x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} 3 - x = 0\\ 3 + x \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 3\\ x = - 3 \end{array} \right. \end{array}$

Vậy phương trình có nghiệm x = 3 hoặc x = -3

$\begin{array}{l} b)\,\,{x^3} - 8 = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x - 2 = 0\\ {x^2} + 2x + 4 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 2\\ {x^2} + 2x + 4 = 0\left( * \right) \end{array} \right. \end{array}$

Giải (* ) ta được:

$\begin{array}{l} {x^2} + 2x + 4 = 0\\ \Leftrightarrow {x^2} + 2x + 1 + 3 = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2} + 3 = 0 \end{array}$

Ta có:

$\begin{array}{l} {\left( {x + 1} \right)^2} \ge 0\,\,\,\,\forall x\\ \Rightarrow {\left( {x + 1} \right)^2} + 3 \ge 3\,\,\,\,\forall x\\ \Rightarrow \,\,{x^2} + 2x + 4 = 0\,\,\,\left( {vn} \right) \end{array}$

Vậy phương trình có nghiệm x = 2

Câu 4: Cho tam giác ABC có D là trung điểm của AC. Qua D kẻ đường thẳng DF // AB và DE // BC

a) Chứng minh BDEF là hình bình hành

b) Gọi K là điểm đối xứng với D qua F. Chứng minh rằng BK // AD

Hướng dẫn giải

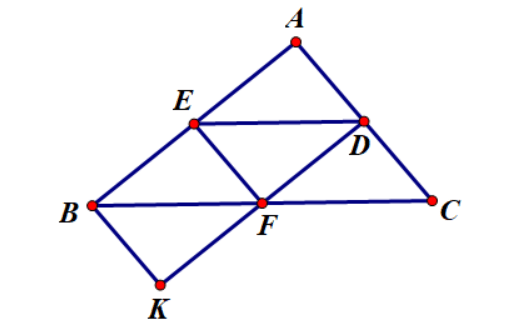
a) Xét tứ giác BDEF có:

$\left\{ \begin{array}{l} DE//BC\\ DF//AB \end{array} \right. \Rightarrow \left\{ \begin{array}{l} DE//BF\\ DF//BE \end{array} \right. \Rightarrow$ tứ giác BDEF là hình bình hành

b) Xét tứ giác ABDK có:

K là điểm đối xứng với D qua F nên KF = FD (1)

Mà $\left\{ \begin{array}{l} DE//BC\\ DA = DC \end{array} \right. \Rightarrow AE = EB$ ( tính chất đường trung bình) (2)

Từ (1) và (2) ta được $\left\{ \begin{array}{l} KF = FD\\ AE = EB \end{array} \right. \Rightarrow$ EF là đường trung bình của tứ giác ABDK

$\Rightarrow EF//BK//AD \Rightarrow BK//AD$

Câu 5: Tìm x, y, z thỏa mãn:

$2{x^2} + 2{y^2} + {z^2} + 25 - 6y - 2xy - 8x + 2z\left( {y - x} \right) = 0$

Hướng dẫn giải

Ta có:

$\begin{array}{l} 2{x^2} + 2{y^2} + {z^2} + 25 - 6y - 2xy - 8x + 2z\left( {y - x} \right) = 0\\ \Leftrightarrow {x^2} + {y^2} + {z^2} - 2xy + 2yz - 2xz + {x^2} - 8x + 16 + {y^2} - 6y + 9 = 0\\ \Leftrightarrow {\left( {x - y - z} \right)^2} + {\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 0 \end{array}$

Ta có:

$\begin{array}{l} {\left( {x - y - z} \right)^2} \ge 0\\ {\left( {x - 4} \right)^2} \ge 0\\ {\left( {y - 3} \right)^2} \ge 0\\ \Rightarrow {\left( {x - y - z} \right)^2} + {\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} \ge 0 \end{array}$

Dấu “ =’’ xảy ra khi $\left\{ \begin{array}{l} {\left( {x - y - z} \right)^2} = 0\\ {\left( {x - 4} \right)^2} = 0\\ {\left( {y - 3} \right)^2} = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 4\\ y = 3\\ z = 1 \end{array} \right.$

Vậy $\left( {x;y;z} \right) = \left( {4;3;1} \right)$

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 11

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 11)

Câu 1: Phân tích đa thức thành nhân tử:

$\begin{array}{l} a)\,\,\,\,5x\left( {7 - x} \right) - 6\left( {x - 7} \right)\\ b)\,\,\,\,36 - 9{y^2}\\ c)\,{x^2} - 2x + 1 - {y^2}\\ d)\,\,{x^2} - 6x + 8 \end{array}$

Hướng dẫn giải

$\begin{array}{l} a)\,\,\,\,5x\left( {7 - x} \right) - 6\left( {x - 7} \right)\\ = 5x\left( {7 - x} \right) + 6\left( {7 - x} \right)\\ = \left( {7 - x} \right)\left( {5x + 6} \right)\\ b)\,\,\,\,36 - 9{y^2}\\ = {6^2} - {\left( {3y} \right)^2} = \left( {6 - 3y} \right)\left( {6 + 3y} \right)\\ = 3\left( {2 - y} \right).3\left( {2 + y} \right) = 9\left( {2 - y} \right)\left( {2 + y} \right)\\ c)\,{x^2} - 2x + 1 - {y^2}\\ = {\left( {x - 1} \right)^2} - {y^2} = \left( {x - 1 - y} \right)\left( {x - 1 + y} \right)\\ d)\,\,{x^2} - 6x + 8\\ = {x^2} - 4x - 2x + 8\\ = x\left( {x - 4} \right) - 2\left( {x - 4} \right)\\ = \left( {x - 4} \right)\left( {x - 2} \right) \end{array}$

Câu 2: Tìm x biết

$\begin{array}{l} a)\,\left( {x - 1} \right)\left( {x + 5} \right) - {\left( {x + 3} \right)^2} + 14 = 0\\ b)\,\,{x^2} + 3x - 4 = 0 \end{array}$

Hướng dẫn giải

$\begin{array}{l} a)\,\left( {x - 1} \right)\left( {x + 5} \right) - {\left( {x + 3} \right)^2} + 14 = 0\\ \Leftrightarrow {x^2} + 5x - x + 5 - {x^2} - 6x - 9 + 14 = 0\\ \Leftrightarrow - x + 10 = 0\\ \Leftrightarrow x = 10 \end{array}$

Vậy phương trình có tập nghiệm $S = \left\{ {10} \right\}$

$\begin{array}{l} b)\,\,{x^2} + 3x - 4 = 0\\ \Leftrightarrow {x^2} + 4x - x - 4 = 0\\ \Leftrightarrow x\left( {x + 4} \right) - \left( {x + 4} \right) = 0\\ \Leftrightarrow \left( {x + 4} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} \left( {x + 4} \right) = 0\\ \left( {x - 1} \right) = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 4\\ x = 1 \end{array} \right. \end{array}$

Vậy phương trình có nghiêm x = - 4 hoặc x = 1

Câu 3: Chứng minh rằng giá trị biểu thức sao không phụ thuộc vào giá trị của biến:

${\left( {2x - 3} \right)^2} - \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right) + x\left( {{x^2} - 4x + 16} \right)$

Hướng dẫn giải

Ta có:

$\begin{array}{l} {\left( {2x + 3} \right)^2} - \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right) + x\left( {{x^2} - 4x - 12} \right)\\ = 4{x^2} + 12x + 9 - {x^3} + 8 + {x^3} - 4{x^2} - 12x\\ = 17 \end{array}$

Vậy giá trị biểu thức sao không phụ thuộc vào giá trị của biến

Câu 4: Cho tam giác ABC vuông tại A, trung tuyến AD, đường cao AH. Gọi M, N lần lượt là chân các đường vuông góc hạ từ D lên AB và AC. Chứng minh:

a) AD = MN

b) Tứ giác DMNC là hình bình hành

c) A đối xứng với H qua MN

Hướng dẫn giải

a) Xét tứ giác AMND có:

$\begin{array}{l} \widehat {BAC} = {90^ \circ }\left( {AB \bot AC} \right)\\ \widehat {DMA} = {90^ \circ }\left( {DM \bot AB} \right)\\ \widehat {DNA} = {90^ \circ }\left( {DN \bot AC} \right)\\ \Rightarrow \widehat {BAC} = \widehat {DMA} = \widehat {DNA} = {90^ \circ } \end{array}$

Tứ giác AMDN là hình chữ nhật $\Rightarrow AD = MN$ ( đường chéo hình chữ nhật)

b) Ta có: $\left\{ \begin{array}{l} DM \bot AB\\ AB \bot NC \end{array} \right. \Rightarrow DM//NC$ (1)

Lại có: $AD = DC = BD = \frac{1}{2}BC \Rightarrow \Delta ADC$ và $\Delta ADB$ cân

Xét tam giác ADC có:

DN là đường cao đồng thời là đường trung tuyến $\Rightarrow AN = NC$

Mà $AN = MD$ ( tính chất hình chữ nhật)

$\Rightarrow NC = MD$ (2)

Từ (1) và (2) ta được tứ giác DMNC là hình bình hành

Xét tam giác ADB có:

DM là đường cao đồng thời là đường trung tuyến $\Rightarrow AM = MB$

Xét tam giác ABC có:

M là trung điểm của AB

N là trung điểm của AC

Suy ra MN là đường trung bình của tam giác ABC

$MN//BC$

Lại có: $\left\{ \begin{array}{l} AH \bot BC\\ MN//BC \end{array} \right. \Rightarrow MN \bot AH$ tại I (1)

Xét tam giác AHC có: $\left\{ \begin{array}{l} NA = NC\\ MN//BC \end{array} \right. \Rightarrow IA = IH$ ( tính chất đường trung bình) (2)

Từ (1) và (2) ta được A đối cứng với H qua MN tại I

Câu 5: Tìm giá trị nhỏ nhất của biểu thức: $2{x^2} + {y^2} + 2xy - 14x - 6y + 50$

Hướng dẫn giải

Ta có:

$\begin{array}{l} 2{x^2} + {y^2} + 2xy - 14x - 6y + 50\\ = {x^2} + 2xy + {y^2} + 6x - 6y + 9 + {x^2} - 20x + 100 + 59\\ = {\left( {x + y - 3} \right)^2} + {\left( {x - 10} \right)^2} + 59 \end{array}$

Ta có:

$\begin{array}{l} \left\{ \begin{array}{l} {\left( {x + y - 3} \right)^2} \ge 0\,\,\,\,\,\,\,\left( {\forall x,y} \right)\\ {\left( {x - 10} \right)^2} \ge 0\,\,\,\,\,\,\,\,\,\,\,\,\,\forall x \end{array} \right.\\ \Rightarrow {\left( {x + y - 3} \right)^2} + {\left( {x - 10} \right)^2} \ge 0\\ \Rightarrow {\left( {x + y - 3} \right)^2} + {\left( {x - 10} \right)^2} + 59 \ge 59 \end{array}$

Vậy GTNN của biểu thức là 59 khi $\left\{ \begin{array}{l} x + y - 3 = 0\\ x - 10 = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 10\\ y = 7 \end{array} \right.$

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 12

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 12)

I. Trắc nghiệm

Câu 1: Khai triển hằng đẳng thức ta được kết quả

A. ${\left( {x - 2y} \right)^3}$

B. ${x^3} - 2{y^3}$

C. ${x^3} - 6{x^2}y + 12x{y^2} - 8{y^3}$

$\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right)$

Câu 2: Kết quả của phép tính $- {x^2}\left( {3 - 2x} \right)$ là

A. $3{x^2} - 2{x^3}$

B. $2{x^3} - 3{x^2}$

C. $- 3{x^2} + 2{x^3}$

D. $- 4{x^2}$

Câu 3: Để thành một hẳng đẳng thức thì giá trị của $4{y^2} - 8y + ....$ …là

A. 4

B.9

C.16

D.25

Câu 4: Giá trị của biểu thức ${1001^2} - 1$ là

A. ${1000^2}$

B. $1002000$

C. 1000

D. 100200

Câu 5: Tìm x biết $4{x^2} - 9 = 0$ . Giá trị của x là

A. $\frac{2}{3};\frac{{ - 2}}{3}$

B. $\frac{3}{2};\frac{{ - 2}}{3}$

C. $\frac{3}{2};\frac{{ - 3}}{2}$

D. $\frac{2}{3};\frac{{ - 3}}{2}$

B. Tự luận

Câu 1: Phân tích đa thức thành nhân tử

$a)\,\,\,36{a^4} - {x^2}$

$b)\,\,\,{x^2} - 2x + 1 - {y^2}$

Câu 2: Tìm x biết

$a)\,\,\,x\left( {x - 4} \right) + 1 = 3x - 5$

$b)\,\,\,2{x^3} - {x^2} - 2x + 1 = 0$

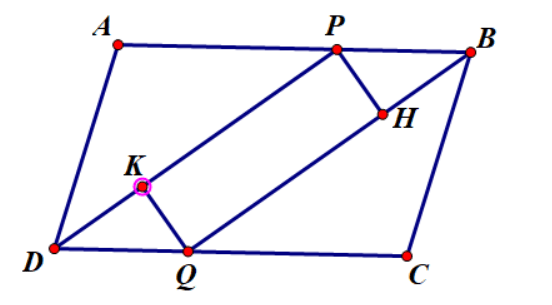
Câu 3: Cho hình bình hành ABCD có AB > BC. Đường phân giác góc D cắt AB tại P, đường phân giác góc B cắt CD tại Q.

a) Chứng minh rằng AP = CQ

b) Chứng minh tứ giác DPBQ là hình bình hành.

c) Gọi H, K lần lượt là hình chiếu của P và Q trên BQ và DP. Chứng minh rằng hai đoạn thẳng AC và PQ cắt nhau tại trung điểm của mỗi đường.

Câu 4: Tìm giá trị nhỏ nhất của biểu thức: $A = - 2{x^2} - 10{z^2} + 4xz + 4x + 4z + 2016$

Đáp án đề thi Toán giữa kỳ 1 lớp 8

1. Phần trắc nghiệm

1. D

2.C

3. A

4.B

5.C

2. Phần tự luận

Câu 1:

$a)\,\,\,36{a^4} - {x^2} = {\left( {6{a^2}} \right)^2} - {x^2} = \left( {6{a^2} - x} \right)\left( {6{a^2} + x} \right)$

$b)\,\,\,{x^2} - 2x + 1 - {y^2} = {\left( {x - 1} \right)^2} - {y^2} = \left( {x - 1 - y} \right)\left( {x - 1 + y} \right)$

Câu 2:

$\begin{array}{l} a)\,\,\,x\left( {x - 4} \right) + 1 = 3x - 5 \Leftrightarrow {x^2} - 4x + 1 - 3x + 5 = 0\\ \Leftrightarrow {x^2} - 7x + 6 = 0\\ \Leftrightarrow {x^2} - 6x - x + 6 = 0\\ \Leftrightarrow x\left( {x - 6} \right) - \left( {x - 6} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x - 1 = 0}\\ {x - 6 = 0} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1}\\ {x = 6} \end{array}} \right. \end{array}$

Vậy phương trình có nghiệm $x = 1$ hoặc $x = 6$

$\begin{array}{l} b)\,\,\,2{x^3} - {x^2} - 2x + 1 = 0\\ \Leftrightarrow \left( {2{x^3} - {x^2}} \right) - \left( {2x - 1} \right) = 0\\ \Leftrightarrow {x^2}\left( {2x - 1} \right) - \left( {2x - 1} \right) = 0\\ \Leftrightarrow \left( {2x - 1} \right)\left( {{x^2} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = \frac{1}{2}\\ x = 1\\ x = - 1 \end{array} \right. \end{array}$

Vậy phương trình có nghiệm $x = \frac{1}{2}$ hoặc $x = 1$ , hoặc $x = - 1$

Câu 3:

a) Xét tam giác ADP và tam giác QBC có:

$\left\{ \begin{array}{l} AD = BC\\ \widehat {ADP} = \widehat {CBQ} = \frac{1}{2}\widehat {ADC}\\ \widehat {DAB} = \widehat {BCD} \end{array} \right.$

b) Ta có $\left\{ \begin{array}{l} AB = AP + PB\\ DC = QC + DQ \end{array} \right.$ mà $\left\{ \begin{array}{l} AB = DC\\ AP = QC \end{array} \right. \Rightarrow PB = DQ$

Lại có $AB//CD \Rightarrow PB//DQ$ nên PBDQ là hình bình hành

c) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD O là trung điểm của DB, O là trung điểm của AC

Gọi O’ là giao điểm của hai đường chéo của hình bình hành PBDQ O’ là trung điểm của DB, O là trung điểm của PQ

Nên O là giao điểm của AC và PQ và cắt nhau tại trung điểm O của mỗi đường

Câu 4:

$\begin{array}{l} A = - 2{x^2} - 10{z^2} + 4xz + 4x + 4z + 2016\\ = - 2\left[ {{x^2} - 2x\left( {y + 1} \right) + {{\left( {y + 1} \right)}^2} + \left( {4{y^2} - 4y + 1} \right) - 1010} \right]\\ = - 2{\left( {x - y - 1} \right)^2} - 2{\left( {2y - 1} \right)^2} + 2020 \end{array}$

Vậy GTLN của A bằng 2020 khi $y = \frac{1}{2};\,\,x = \frac{3}{2}$

Đề thi Toán lớp 8 Giữa kì 1 năm 2022 - 2023 có đáp án (20 Đề) - Đề 13

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 13)

Câu 1 (2 điểm) Phân tích đa thức thành nhân tử

$a. 2{{x}^{2}}-3x-2$	$b. 4x\left( x-2 \right)+3\left( 2-x \right)$
$c. 27{{x}^{3}}+8$	$d. {{x}^{2}}+2x-{{y}^{2}}+1$

Câu 2 (2 điểm) Tìm giá trị của x, biết:

$a. 9{{x}^{2}}+6x-3=0$
$b. x\left( x-2 \right)\left( x+2 \right)-\left( x+2 \right)\left( {{x}^{2}}-2x+4 \right)=4$
Câu 3 (2 điểm) Rút gọn và tính giá trị biểu thức:

với

b. tại

Câu 4 (3,5 điểm) Cho tam giác ABC cho N, E lần lượt là trung điểm của các cạnh AB, AC, BC. Chứng minh rằng:

$a. NE=\frac{1}{2}AB$

b. Tứ giác ANEB là hình thang

c. Kẻ đường cao AH. Tính độ dài AH biết NE = 5cm, BH = 6cm

Câu 5 (0,5 điểm) Tính giá trị nhỏ nhất của biểu thức

Đáp án đề thi giữa học kì 1 môn Toán 8

Câu 1:

a. (0,5 điểm)

$\begin{align} & 2{{x}^{2}}-3x-2=2{{x}^{2}}-4x+x-2=\left( 2{{x}^{2}}-4x \right)+\left( x-2 \right) \\ & =2x\left( x-2 \right)+\left( x-2 \right)=\left( x-2 \right)\left( 2x+1 \right) \\ \end{align}$

b. (0,5 điểm)

$4x\left(x-2\right)+3\left(2-x\right)=4x\left(x-2\right)-3\left(x-2\right)=\left(x-2\right)\left(4x-3\right)$

c. (0.5 điểm)

$27{{x}^{3}}+8={{\left( 3x \right)}^{3}}+{{2}^{3}}=\left( 3x+2 \right)\left[ {{\left( 3x \right)}^{2}}-2.3x+{{2}^{2}} \right]=\left( 3x+2 \right)\left( 9{{x}^{2}}-6x+2 \right)$

d. (0,5 điểm)

$\begin{align} & {{x}^{2}}+2x-{{y}^{2}}+1=\left( {{x}^{2}}+2x+1 \right)-{{y}^{2}}={{\left( x+1 \right)}^{2}}-{{y}^{2}} \\ & =\left( x+1-y \right)\left( x+1+y \right) \\ \end{align}$

Câu 2:

a. (1 điểm)

$\begin{align} & 9{{x}^{2}}+6x-3=0 \\ & \Leftrightarrow 3\left( 3{{x}^{2}}+2x-1 \right)=0 \\ & \Leftrightarrow 3\left( 3{{x}^{2}}-x+3x-1 \right)=0 \\ & \Leftrightarrow 3\left[ x\left( 3x-1 \right)+\left( 3x-1 \right) \right]=0 \\ & \Leftrightarrow 3\left( x+1 \right)\left( 3x-1 \right)=0 \\ \end{align}$

Suy ra $x=\frac{-1}{3}$ hoặc $x=-1$

Vậy $x=\frac{-1}{3}$ hoặc $x=-1$

b. (1 điểm)

$\begin{align} & x\left( x-2 \right)\left( x+2 \right)-\left( x+2 \right)\left( {{x}^{2}}-2x+4 \right)=4 \\ & \Leftrightarrow x\left( {{x}^{2}}-4 \right)-\left( {{x}^{3}}+8 \right)=4 \\ & \Leftrightarrow {{x}^{3}}-4x-{{x}^{3}}-8-4=0 \\ & \Leftrightarrow -4x=12 \\ & \Leftrightarrow x=-3 \\ \end{align}$

Suy ra x = -3

Vậy x = -3

Câu 3:

a. (1 điểm)

$A=x\left( x+y \right)-5\left( x+y \right)=\left( x+y \right)\left( x-5 \right)$ (*)

Thay $x=1,y=2$ vào biểu thức (*) ta có:

$A=\left( 1+2 \right)\left( 1-5 \right)=3.\left( -4 \right)=-12$

Vậy với thì A = -12

b. (1 điểm)

$\begin{align} & B=3x\left( {{x}^{2}}-3 \right)+{{x}^{2}}\left( 4-3x \right)-4{{x}^{2}}+1 \\ & B=3{{x}^{3}}-9x+4{{x}^{2}}-3{{x}^{3}}-4{{x}^{2}}+1 \\ & B=-9x+1 \\ \end{align}$

Thay $x=\frac{1}{9}$ vào biểu thức B ta có

$B=-9.\frac{1}{9}+1=0$

Vậy khi $x=\frac{1}{9}$ thì B = 0

Câu 4: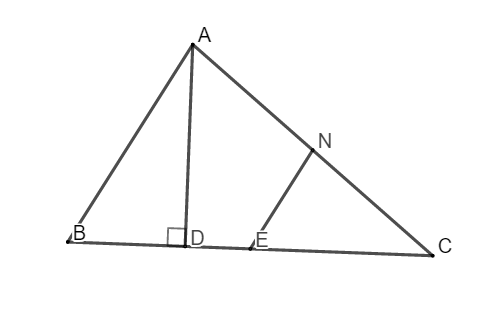 Đề kiểm tra giữa học kì 1 môn Toán lớp 8 năm học 2020 - 2021 Đề 1

a. Ta có N là trung điểm của AC nên AN = NC

E là trung điểm của BC nên BE = EC

Suy ra NE là đường trung bình của tam giác ABC

Theo tính chất của đường trung bình ta có:

NE // AB và

b. Từ chứng minh câu a có NE // AB nên tứ giác AENB là hình thang

c. Ta có NE = 5cm suy ra AB = 2NE = 10cm (chứng minh câu a)

Xét tam giác AHB vuông tại H

Áp dụng định lý Pi – ta – go ta có:

$\begin{align} & A{{B}^{2}}=A{{H}^{2}}+B{{H}^{2}} \\ & \Rightarrow A{{H}^{2}}=A{{B}^{2}}-B{{H}^{2}}={{10}^{2}}-{{6}^{2}}={{8}^{2}} \\ & \Rightarrow AH=8cm \\ \end{align}$