Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 3 Bài 2: Phương trình bậc nhất một ẩn và cách giải. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 2Phương trình bậc nhất một ẩn và cách giải. Mời các bạn đón xem:
Bài tập Toán 8 Chương 3 Bài 2: Phương trình bậc nhất một ẩn và cách giải
A. Bài tập Phương trình bậc nhất một ẩn và cách giải
I. Bài tập trắc nghiệm
Bài 1: Nghiệm của phương trình 2x - 1 = 3 là ?
A. x = - 2.
B. x = 2.
C. x = 1.
D. x = - 1.
Hướng dẫn:
Ta có: 2x - 1 = 3 ⇔ 2x = 1 + 3 ⇔ 2x = 4
⇔ x = ⇔ x = 2.
Vậy nghiệm của phương trình là x = 2.
Chọn đáp án B.
Bài 2: Nghiệm của phương trình + 3 = 4 là?
A. y = 2.
B. y = - 2.
C. y = 1.
D. y = - 1.
Hướng dẫn:
Ta có: + 3 = 4 ⇔ = 4 - 3 ⇔ = 1
⇔ y = 2.1 ⇔ y = 2.
Vậy nghiệm của phương trình là y = 2.
Chọn đáp án A.
Bài 3: Giá trị của m để phương trình 2x = m + 1 có nghiệm x = - 1 là ?
A. m = 3.
B. m = 1.
C. m = - 3
D. m = 2.
Hướng dẫn:
Phương trình 2x = m + 1 có nghiệm x = - 1
Khi đó ta có: 2.( - 1 ) = m + 1 ⇔ m + 1 = - 2 ⇔ m = - 3.
Vậy m = - 3 là giá trị cần tìm.
Chọn đáp án C.
Bài 4: Tập nghiệm của phương trình - 4x + 7 = - 1 là?
A. S = { 2 }.
B. S = { - 2 }.
C. S = { }.
D. S = { 3 }.
Hướng dẫn:
Ta có: - 4x + 7 = - 1 ⇔ - 4x = - 1 - 7 ⇔ - 4x = - 8
⇔ x = ⇔ x = 2.
Vậy phương trình có tập nghiệm là S = { 2 }.
Chọn đáp án A.
Bài 5: x = là nghiệm của phương trình nào sau đây?
A. 3x - 2 = 1.
B. 2x - 1 = 0.
C. 4x + 3 = - 1.
D. 3x + 2 = - 1.
Hướng dẫn:
+ Đáp án A: 3x - 2 = 1 ⇔ 3x = 3 ⇔ x = 1 → Loại.
+ Đáp án B: 2x - 1 = 0 ⇔ 2x = 1 ⇔ x = → Chọn.
+ Đáp án C: 4x + 3 = - 1 ⇔ 4x = - 4 ⇔ x = - 1 → Loại.
+ Đáp án D: 3x + 2 = - 1 ⇔ 3x = - 3 ⇔ x = - 1 → Loại.
Chọn đáp án B.
Bài 6: Giải phương trình:
A. x = 2
B. x = 1
C. x = -2
D. x = -1
Chọn đáp án A
Bài 7: Giải phương trình: 4x - 2(x + 1) = 3x + 2
A. x = 2
B. x = -3
C. x = - 4
D. x = 5
Chọn đáp án C
Bài 8: Tìm số nghiệm của phương trình sau: x + 2 - 2(x + 1) = -x
A. 0
B.1
C. 2
D. Vô số
Ta có: x + 2 - 2(x + 1) = -x
⇔ x + 2 - 2x - 2 = -x
⇔ -x = -x ( luôn đúng với mọi x)
Do đó, phương trình đã cho có vô số nghiệm.
Chọn đáp án D
Bài 9: Tìm tập nghiệm của phương trình sau: 2(x + 3) - 5 = 4 – x
A. S = {1}
B. S = 1
C. S = {2}
D. S = 2
Lời giải:
Chọn đáp án A
Bài 10: Phương trình sau có 1 nghiệm 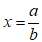
A. 22 B. 17
C. 27 D. 20
Lời giải:
Chọn đáp án C
II. Bài tập tự luận có lời giải
Bài 1: Phương trình 2x – 3 = 12 – 3x có bao nhiêu nghiệm?
Lời giải
Ta có 2x – 3 = 12 – 3x
⇔ 2x + 3x = 12 + 3
⇔ 5x = 15
⇔ x = 15 : 5
⇔ x = 3
Vậy phương trình có một nghiệm duy nhất x = 3
Bài 2 Số nghiệm của phương trình (x – 1)2 = x2 + 4x – 3 là:
Lời giải
(x – 1)2 = x2 + 4x – 3
⇔ x2 – 2x + 1 = x2 + 4x – 3
⇔ x2 – 2x + 1 – x2 – 4x + 3 = 0
⇔ -6x + 4 = 0
⇔ x =
Vậy phương trình có nghiệm duy nhất x =
Bài 3 Cho biết 2x – 2 = 0. Tính giá trị của 5x2 – 2.
Lời giải
Ta có
2x – 2 = 0
⇔ 2x = 2 ⇔ x = 1
Thay x = 1 vào 5x2 – 2 ta được: 5.12 – 2 = 5 – 2 = 3
Bài 4 Giả sử x0 là một số thực thỏa mãn 3 – 5x = -2. Tính giá trị của biểu thức S = ta đươc
Lời giải
Ta có 3 – 5x = -2
⇔ -5x = -2 – 3
⇔ -5x = -5 ⇔ x = 1
Khi đó x0 = 1, do đó S = 5.12 – 1 = 4
Bài 5 Tính giá trị của (5x2 + 1)(2x – 8) biết 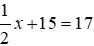
Lời giải
Thay x = 4 vào (5x2 + 1)(2x – 8) ta được: (5.42 + 1)(2.4 – 8) = (5.42 + 1).0 = 0
Bài 6 Giải các phương trình:
a) x – 4 = 0;
b) + x = 0;
c) 0,5 – x = 0.
Hướng dẫn giải chi tiết:
a) x – 4 = 0
⇔ x = 0 + 4
⇔ x = 4
Vậy phương trình có một nghiệm duy nhất x = 4
b) + x = 0
⇔ x = 0-
⇔ x =
Vậy phương trình có một nghiệm duy nhất x=
c) 0,5 – x = 0
⇔ x = 0,5-0
⇔ x = 0,5
Vậy phương trình có một nghiệm duy nhất x = 0,5
Bài 7 Giải các phương trình:
a) = -1;
b) 0,1x = 1,5;
c) -2,5x = 10.
Hướng dẫn giải chi tiết:
a) = -1
⇔ x = (-1).2
⇔ x = -2
Vậy phương trình có một nghiệm duy nhất x = -2
b) 0,1x = 1,5
⇔ x =
⇔ x = 15
Vậy phương trình có một nghiệm duy nhất x = 15
c) -2,5x = 10
⇔ x =
⇔ x = -4
Vậy phương trình có một nghiệm duy nhất x = - 4
Bài 8 Giải phương trình: -0,5x + 2,4 = 0.
Hướng dẫn giải chi tiết:
- 0,5x + 2,4 = 0
⇔ -0,5x = -2,4
⇔ x =
⇔ x = 4,8
Vậy phương trình có một nghiệm duy nhất x = 4,8
Bài 9 Tính diện tích S của hình thang ABCD theo x bằng hai cách:
1) Tính theo công thức: S = BH x (BC + DA) : 2
2) S = SABH + SBCKH + SCKD
Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?
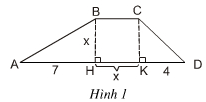
Hướng dẫn giải chi tiết:
1) Công thức: S = BH x (BC + DA) : 2
+ Có BH ⊥ HK, CK ⊥ HK (giả thiết)
Mà BC // HK (vì ABCD là hình thang)
Do đó: BH ⊥ BC, CK ⊥ BC
Tứ giác BCKH có bốn góc vuông nên BCKH là hình chữ nhật.
Mặt khác: BH = HK = x (giả thiết) nên BCKH là hình vuông.
⇒ BH = BC = CK = KH = x
+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.
Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2 =
2) S = SABH + SBCKH + SCKD
+ ABH là tam giác vuông tại H
⇒ SBAH = .BH.AH = .7.x = .
+ BCKH là hình chữ nhật
⇒ SBCKH = x.x = x2.
+ CKD là tam giác vuông tại K
⇒ SCKD = .CK.KD = .4.x = 2x.
Do đó: S = SABH + SBCKH + SCKD = + x2 + 2x = x2 + .
- Với S = 20 ta có phương trình:
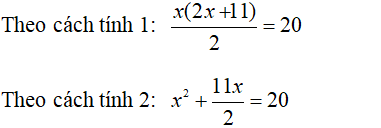
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.
Bài 10 Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:
a) 1 + x = 0
b) x + x2 = 0
c) 1 – 2t = 0
d) 3y = 0
e) 0x – 3 = 0.
Hướng dẫn giải chi tiết:
Phương trình dạng ax+ b= 0, với a, b là hai số đã cho và a ≠ 0 , được gọi là phương trình bậc nhất một ẩn.
+ Phương trình 1 + x = 0 là phương trình bậc nhất với a = 1 ; b = 1.
+ Phương trình x + x2 = 0 không phải phương trình bậc nhất vì có chứa x2 bậc hai.
+ Phương trình 1 – 2t = 0 là phương trình bậc nhất ẩn t với a = -2 và b = 1.
+ Phương trình 3y = 0 là phương trình bậc nhất ẩn y với a = 3 và b = 0.
+ Phương trình 0x – 3 = 0 không phải phương trình bậc nhất vì hệ số bậc nhất a = 0.
Bài 11 Cho phương trình
a) Tìm m để phương trình vô nghiệm.
b) Tìm m để phương trình có nghiệm duy nhất
c) Tìm m để phương trình có vô số nghiệm.
Hướng dẫn giải chi tiết:
a) Để phương trình vô nghiệm thì
Vậy m = -1 thì phương trình vô nghiệm.
b) Để phương trình có nghiệm duy nhất thì
Vậy thì phương trình có nghiệm duy nhất.
c) Để phương trình vô số nghiệm thì
Vậy m = 1 thì phương trình có vô số nghiệm.
Bài 12 Giải các phương trình sau
a) 3x – 6 = 0
b) 2x – x + 4 = 0
c) 8 – 2x = 9 – x
Hướng dẫn giải chi tiết:
a) 3x – 6 = 0
Vậy tập nghiệm của phương trình .
b) 2x – x + 4 = 0
Vậy tập nghiệm của phương trình là .
c) 8 – 2x = 9 – x
Vậy phương trình đã cho có nghiệm .
III. Bài tập vận dụng
Bài 1 Giải các phương trình:
a) 4x – 20 = 0
b) 2x + x + 12 = 0
c) x – 5 = 3 – x
d) 7 – 3x = 9 – x
Bài 2 Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm.
a) 3x – 11 = 0
b) 12 + 7x = 0
c) 10 – 4x = 2x – 3
Bài 3 Giải phương trình x + 3 = 0
Bài 4 Giải phương trình = - 2.
Bài 5 Giải các phương trình
a) 4x – 20 = 0
b) 2x + x + 12 = 0
c) x – 5 = 3 – x
d) 7 – 3x = 9 – x
Bài 6 Giải các phương trình:
a) x – 4 = 0;
b) + x = 0;
c) 0,5 – x = 0.
Bài 7 Giải các phương trình:
a) = -1;
b) 0,1x = 1,5;
c) -2,5x = 10.
Bài 8 Giải phương trình: -0,5x + 2,4 = 0.
B. Lý thuyết Phương trình bậc nhất một ẩn và cách giải
1. Khái niệm
Phương trình bậc nhất một ẩn là phương trình có dạng:
trong đó a, b là hai số đã cho và .
2. Các quy tắc cơ bản
a) Quy tắc chuyển vế:
Khi chuyển vế một hạng tử từ một vế của phương trình sang vế còn lại, ta phải đổi dấu hạng tử đó:
.
b) Quy tắc nhân (hoặc chia) với một số khác 0:
Khi nhân (hoặc chia) hai vế của phương trình với một số khác 0 ta được phương trình mới tương đương với phương trình đã cho:
3. Cách giải phương trình bậc nhất
Ta có:
(sử dụng quy tắc chuyển vế)
(sử dụng quy tắc chia cho )