Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập Liên hệ giữa thứ tự và phép cộng Toán lớp 8, tài liệu bao gồm 3 trang đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Lý thuyết và bài tập Liên hệ giữa thứ tự và phép cộng gồm các nội dung chính sau:

I. Tóm tắt lý thuyết

- tóm tắt lý thuyết ngắn gọn.

II. Bài tập và các dạng bài toán

- gồm 2 dạng Lý thuyết và bài tập Liên hệ giữa thứ tự và phép cộng.

III. Bài tập tự luyện

- gồm 14 bài tập tự luyện giúp học sinh tự rèn luyện cách giải các dạng Lý thuyết và bài tập Liên hệ giữa thứ tự và phép cộng.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

LIÊN HỆ GIỮA THỨ TỰ VÀ PHÉP CỘNG

I. TÓM TẮT LÝ THUYẾT

1. Thứ tự trên tập hợp số

- Mối quan hệ giữa các tập hợp  $\mathbb{N}*\subset \mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset ℝ$

- Biểu đồ Venn

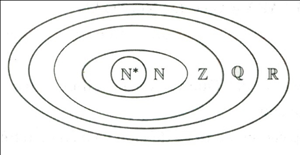
- So sánh hai số a và b trên tập số thực

Chú ý:         $A^2\ge 0$ với mọi A;

                  $-A^2\le 0$  với mọi A;

                  $\left|A\right|\ge 0$  với mọi A là số thực

                   $-\left|A\right|\le 0$  với mọi A là số thực

2. Bất đẳng thức

- Hệ thức dạng $a>b(haya<b;a\ge b;a\le b)$ được gọi là bất đẳng thức; trong đó a và b lần lượt được gọi là vế trái và vế phải.

- Khi cộng cùng một số vào cả hai vế của một bất đẳng thức, ta được bất đẳng thức mới cùng chiều và bất đẳng thức đã cho, cụ thể như sau:

+ Nếu a > b thì a + c > b + c;

+ Nếu a < b thì a + c < b + c;

+ Nếu a ≥ b thì a + c ≥ b + c;

+ Nếu a ≤ b thì a + c ≤ b + c.

II. BÀI TẬP VÀ CÁC DẠNG TOÁN

Dạng 1. Sắp xếp thứ tự các số trên trục số. Biểu diễn mối quan hệ giữa các tập số

Phương pháp giải: Dựa vào các kiến thức cơ bản đã học ở các lớp dưới để làm

1A. Sắp xếp các số sau từ bé đến lớn và biểu diễn trên trục số:

a)  $-2;-4;0,4;\frac{1}{2};\frac{4}{3};\frac{1}{4};$                           b)  $-\sqrt{3};-1;3;\sqrt{6}$

1B. Sắp xếp các số sau từ lớn đến bé  và biểu diễn trên trục số:

a) $-7;-8;-1;-5;0,3,8;$                            b) $-\frac{3}{5};\frac{-1}{2};0;\sqrt{2};\sqrt{5};1$.

2A. Điền các kí hiệu thích hợp vào chỗ trống:

a) $\mathbb{Z}\mathrm{...........}\mathbb{Q}$                              b) $ℝ\cap I=\mathrm{...................}$ 

2B. Điền các kí hiệu thích hợp vào chỗ trống:

a) $ℝ\mathrm{.................}\mathbb{Z}$                                   b)  $I\cap \mathbb{Q}=\mathrm{................}$ 

Dạng 2. Xét tính đúng sai. So sánh

Phương pháp giải: Dựa vào các kiến thức cơ bản, các tính chất, để đưa ra các đánh giá, so sánh.

3A. Hãy xét xem các khẳng định sau đúng hay sai? Vì sao?

a) $(-5)+3>-1$                           b) $2-(-4)>6$;

c) $\frac{1}{3}-3>\frac{1}{2}+4$                            d)  $\frac{x^2}{3}-7\ge -7$

3B. Hãy xét xem các khẳng định sau đúng hay sai? Vì sao?

a)  $-3.\left(2\right)>6$                             b)  $2-\frac{1}{5}<-\frac{1}{5}+2$ 

c) $\left|-2\right|+3<7;$                              d)  $-x^2-1\le 0$

4A. Cho a < b, hãy so sánh:

a) a + 1 và b + 1;                      b) 2 - a và 2 - b

4B. Cho a > b, hãy so sánh

a) a + b và 2b;                          b) 1- a và 1 - b.

5A. Cho m > n, chứng minh:

a) m + 2017 > n + 2016            b) n - 1 < m + 2

5B. Cho m > n, chứng minh:

a) 2019 - n > 2018-m;               b) -1 - m < -n + 2.

6A. Cho x - 8 > 9. Chứng minh x + 3 > 20.

6B. Cho x + 5 > 15. Chứng minh x - 2 > 8.

7A. Cho a > b. Chứng minh a + 1 +  2 + 3 +...+ 9 + 10 > b + 54.

7B. Cho m ≤ n. Chứng minh m + 1+3  + 5 +...+23 + 25 ≤ n + 169.