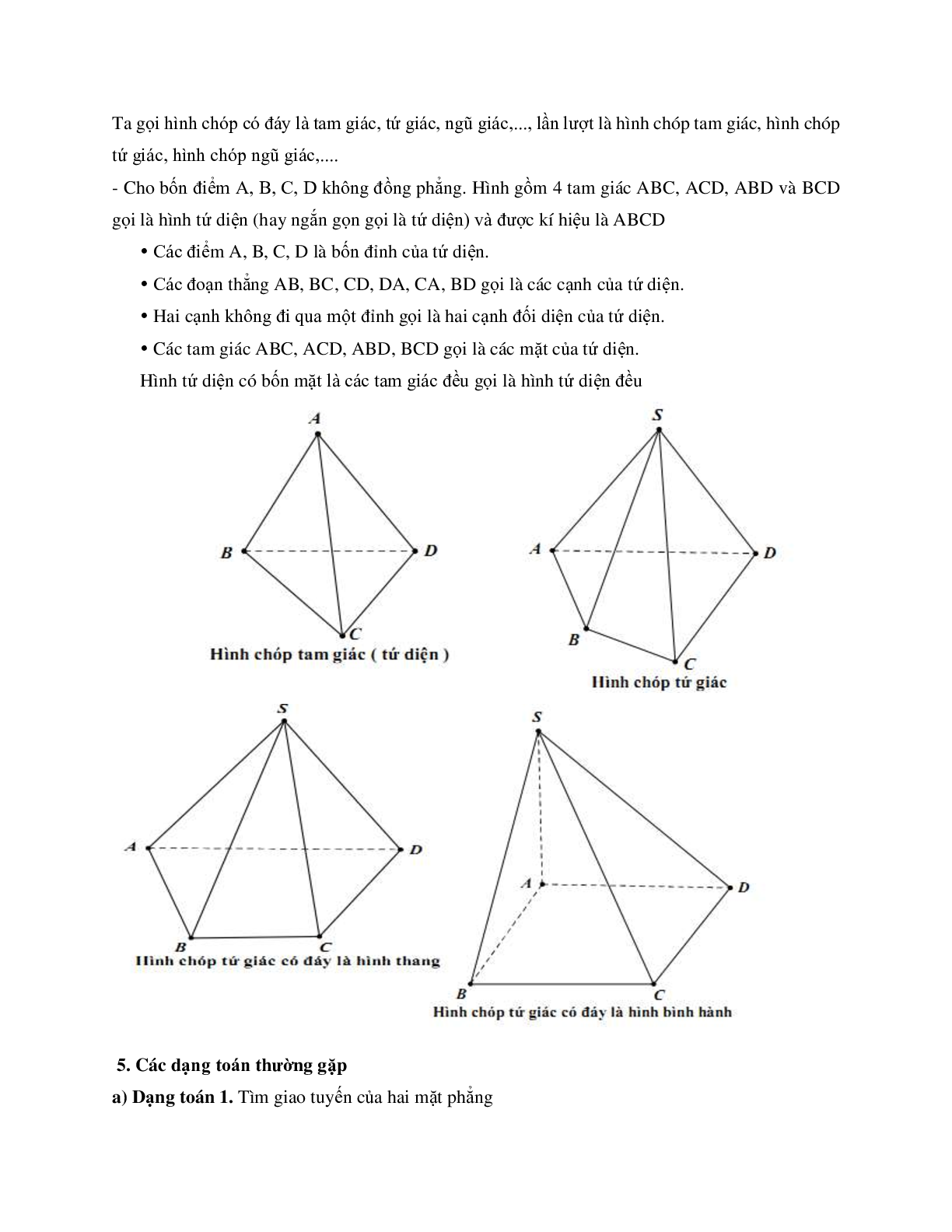
Tailieumoi.vn xin giới thiệu chuyên đề Đại cương về đường thẳng và mặt phẳng thuộc chương trình Toán 11. Chuyên đề gồm 25 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 11.

Chuyên đề Đại cương về đường thẳng và mặt phẳng

Tài liệu gồm các phần sau: 

Phần 1: Lý thuyết

- Tổng hợp kiến thức trọng tâm về Đại cương về đường thẳng và mặt phẳng cần nhớ

Phần 2: Bài tập

- Dạng toán 1. Tìm giao tuyến của hai mặt phẳng: 19 bài tập vận dụng tự luyện 

- Dạng toán 2. Tìm giao điểm của đường thẳng và mặt phẳng: 29 bài tập vận dụng tự luyện 

- Dạng toán 3. Tìm thiết diện của hình (H) khi cắt bởi mặt phẳng (P): 17 bài tập vận dụng tự luyện 

- Dạng toán 4. Chứng minh ba điểm thẳng hàng: 14 bài tập vận dụng tự luyện 

- Dạng toán 5. Chứng minh ba đường thẳng đồng quy: 7 bài tập vận dụng tự luyện 

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BÀI 1: ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG

1. Mở đầu về hình học không gian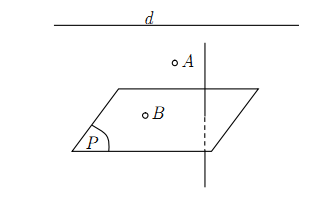

- Đối tượng cơ bản:

+ Điểm: kí hiệu A, B, C, …

+ Đường thẳng: kí hiệu a, b, c, d, …

+ Mặt phẳng: kí hiệu $\left(\mathrm{P}\right),\left(\mathrm{Q}\right),\left(\mathrm{\alpha }\right),\left(\mathrm{\beta }\right),\mathrm{\dots }$

- Quan hệ cơ bản:

 + Thuộc: kí hiệu $\in$  .Ví dụ:  $\mathrm{A}\in \mathrm{d},\mathrm{M}\in \left(\mathrm{P}\right)$

 + Chứa, nằm trong: kí hiệu $\subset$ .Ví dụ:  $\mathrm{d}\subset \left(\mathrm{P}\right),\mathrm{b}\subset \left(\mathrm{\alpha }\right)$

- Hình biểu diễn của một hình trong không gian:

+ Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng biểu diễn bởi đoạn thẳng.

+ Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song (hoặc cắt nhau)

+ Hai đoạn thẳng song song hoặc bằng nhau được biểu diễn bởi hai đoạn thẳng song song và bàng nhau.

+ Dùng nét vẽ liền (__) để biểu diễn cho những đường trông thấy và dùng nét đứt đoạn (----) để biểu diễn cho những đường bị che khuất.

2. Các tính chất thừa nhận trong hình học không gian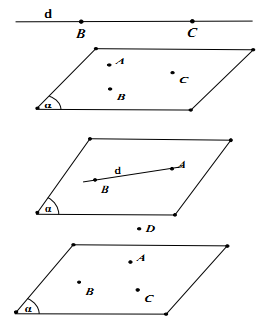

- Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt không thẳng hàng cho trước.

- Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

- Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

- Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

- Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa. Từ tính chất này suy ra: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy. Đường thẳng chung là duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng chung đó được gọi là giao tuyến của hai mặt phẳng.

- Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

3. Điều kiện xác định mặt

- Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.

- Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.

- Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.

Mặt phẳng hoàn toàn có thể mở rộng ra đến vô cực