Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Đường thẳng và mặt phẳng trong không gian quan hệ song song, tài liệu bao gồm 53 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

§1. Đại cương về đường thẳng và mặt phẳng

§2. Hai đường thẳng chéo nhau và hai đường thẳng song song

§3. Đường thẳng và mặt phẳng song song

§4. Hai mặt phẳng song song

§5. Phép chiếu song song

Ôn tập chương II

Trắc nghiệm chương II

Một số đề ôn kiểm tra 1 tiết

Đường thẳng và mặt phẳng trong không gian quan hệ song song

Chương II Đường thẳng và mặt phẳng trong không gian quan hệ song song

§1. Đại cương về đường thẳng và mặt phẳng

A. Kiến thức cần nắm

I. Các tính chất thừa nhận

Tính chất 1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt .

Tính chất 2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

Tính chất 3 . Nếu đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Lưu ý: Đường thẳng d nằm trong \(mp(\alpha )\) ta kí hiệu: \(d \subset (\alpha )\) hay \((\alpha ) \supset d\)

Tính chất 4. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

Tính chất 5 . Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.

Như vậy: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung đi qua điểm chung ấy và đường thẳng đó gọi là giao tuyến của hai mặt phẳng.

Tính chất 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

II. Cách xác định mặt phẳng.

Một mặt phẳng hoàn toàn xác định khi biết:

1. Nó đi qua ba điểm không thẳng hàng

(ABC) biểu thị mặt phẳng xác định bởi ba điểm phân biệt không thẳng hàng A, B, C.

2. Nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó (M,d) biểu thị mặt phẳng xác định bởi đường thẳng d và điểm M không nằm trên D.

3. Nó chứa hai đường thẳng cắt nhau (a,b) biểu thị mặt phẳng xác định bởi hai đường thẳng cắt nhau a và b.

III. Hình chóp và hình tứ diện

1. Hình chóp : Trong mặt phẳng \((\alpha )\) cho đa giác lồi \({A_1}{A_2} \ldots {A_n}\).

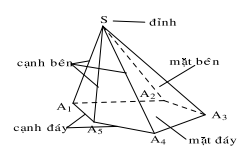
Điểm S nằm ngoài \((\alpha )\). Lần lượt nối S với các đỉnh \({A_1},{A_2}, \ldots ,{A_n}\) ta được n tam giác \(S{A_1}{A_2},S{A_2}{A_3}, \ldots ,S{A_n}{A_1}\). Hình gồm có đa giác \({A_1}{A_2} \ldots {A_n}\) và \(n\) tam giác \(S{A_1}{A_2},S{A_2}{A_3}, \ldots ,S{A_n}{A_1}\) được gọi là hình chóp , kí hiệu \(S \cdot {A_1}{A_2} \ldots {A_n}\)

2. Hình tứ diện

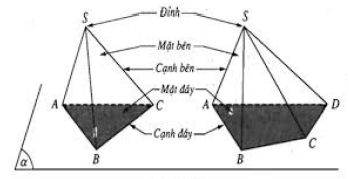
Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ABD, ACD và BCD được gọi là hình tứ diện , kí hiệu ABCD.

B. Bài tập

Vấn đề 1. Tìm giao tuyến của hai mặt phẳng

Phương pháp: Ta đi tìm hai điểm chung phân biệt của hai mặt phẳng đó. Giao tuyến của chúng là đường thẳng đi qua hai điểm đó.

Nghĩa là:\({\rm{ }}\left\{ {\begin{array}{*{20}{l}}{\alpha  \cap \beta  = M}\\{\alpha  \cap \beta  = N \Rightarrow \alpha  \cap \beta  = MN}\\{M \ne N}\end{array}} \right.\)

Bài 1.1. Cho bốn điểm không đồng phẳng A,B,C và D. Trên đoạn AB và AC lấy hai điểm M và N sao cho \(\frac{{AM}}{{BM}} = 1;\frac{{AN}}{{NC}} = 2\). Hãy xác định giao tuyến của mặt phẳng (DMN) với các mặt (ABD),(ACD),(ABC) và (BCD).

Hướng dẫn giải:

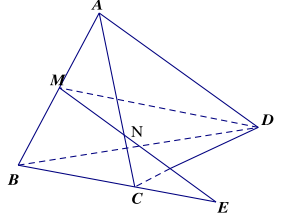
* \((DMN) \cap (ADB) = \) ?

Ta có \(D \in (DMN) \cap (ADB)\)

\(\left. {\begin{array}{*{20}{l}}{M \in (DMN)}\\{M \in AB \subset (ABD) \Rightarrow M \in (ABD)}\end{array}} \right\} \Rightarrow M \in (DMN) \cap (ABD)\)

Vậy: \(DM = (DMN) \cap (ABD)\)

* \((DMN) \cap (ACD) = DN\)

* \((DMN) \cap (ABC) = MN\)

\( \star (DMN) \cap (BCD) = \) ?

Trong mp(ABC) có \(\frac{{AM}}{{BM}} \ne \frac{{AN}}{{NC}}\), nên \(MN \cap BC = E\)

Tương tự: \((DMN) \cap (BCD) = DE\)

Bài 1.2. Cho S là một điểm không thuộc mặt phẳng hình bình hành ABCD. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).

Hướng dẫn giải

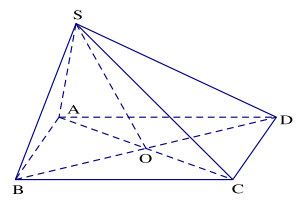
Gọi O là giao điểm của AC và BD. Ta có \(S \in (SAC) \cap (SBD)\)

\(\left. {\begin{array}{*{20}{l}}{O \in AC \subset (SAC)}\\{O \in BD \subset (SBD)}\end{array}} \right\} \Rightarrow O \in (SAC) \cap (SBD)\)

nên \(SO = (SAC) \cap (SBD)\)

Vậy giao tuyến hai mặt phẳng (SAC) và (SBD) là đường thẳng SO.

Bài 1.3. Cho S là một điểm không thuộc mặt phẳnh hình thang ABCD(AB//CD) và AB > CD. Tìm giao tuyến hai mặt phẳng (SAD) và (SBC).

Hướng dẫn giải

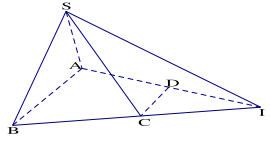
Gọi I là giao điềm AD và BC. Ta có S và I là hai điểm chung của (SAD) và (SBC), nên \(SI = (SAD) \cap (SBC)\)

Vậy giao tuyến hai mặt phẳng (SAD) và (SBC) là đường thẳng SI.

Bài 1.4. Cho bốn điểm A, B, C, D không đồng phẳng. Gọi I, K lần lượt là trung điểm của hai đoạn thẳng AD và BC.

a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD)

b) Gọi M và N là hai điểm lần lượt trên hai đường thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).

Hướng dẫn giải

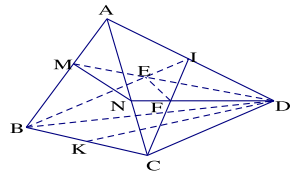
a) \((IBC) \cap (KAD) = KI\). Vậy giao tuyến hai mặt phẳng (IBC) và (KAD) là đường thẳng KI.

b) Trong mp (ABD), gọi \(E = MD \cap BI\), trong mp(ACD), gọi \(F = ND \cap CI\)

Ta có:

\((IBC) \cap (DMN) = EF\)

Vậy giao tuyến hai mặt phẳng (IBC) và (DMN) là đường thẳng EF.

Vấn đề 2. Tìm giao điểm của đường thẳng d và mặt phẳng \((\alpha )\)

Phương pháp: Để tìm giao điểm của một đường thẳng d và một mặt phẳng \((\alpha )\), ta có thể đưa về việc tìm giao điểm của đường thẳng d với một đường thẳng \({d^\prime }\) nằm trong mặt phẳng \((\alpha )\)

Nghĩa là \(\left. {\begin{array}{*{20}{l}}{mpphu(\beta ) \supset d}\\{(\beta ) \cap (\alpha ) = {d^\prime }}\\{{d^\prime } \cap d = I}\end{array}} \right\} \Rightarrow d \cap (\alpha ) = I\)

Bài 1.5. Cho tam giác BCD và điểm A không thuộc mặt phẳng (BCD). Gọi K là trung điểm của đoạn AD và G là trọng tâm của tam giác ABC. Tìm giao điểm của đường thẳng GK với mặt phẳng (BCD).

Hướng dẫn giải

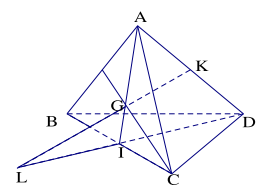
Gọi J là giao điểm của AG và BC. Trong mặt phẳng (AJD), ta có \(\frac{{AG}}{{AJ}} = \frac{2}{3};\frac{{AK}}{{AD}} = \frac{1}{2}\) nên GK và JD cắt nhau. Gọi L là giao điểm của GK và JD.

Ta có \(L \in GK\)

\(\left\{ {\begin{array}{*{20}{l}}{L \in JD}\\{JD \subset (BCD)}\end{array} \Rightarrow L \in (BCD)} \right.\)

Vậy L là giao điểm của GK và (BCD)

Bài 1.6. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và CD, trên AD lấy điểm P không trùng với trung điểm AD

a) Gọi E là giao điểm của đường thẳng MP và BD. Tìm giao tuyến của hai mp (PMN) và (BCD)

b) Tìm giao điểm của hai mp(PMN) và BC.

Hướng dẫn giải

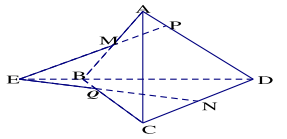
a) \((MNP) \cap (BCD) = EN\)

b) Trong mp (BCD), gọi \(Q = EN \cap BC\)

Ta có \(:BC \cap (MNP) = Q\)

Bài 1.7. Cho tứ diện ABCD. Gọi I, J là các điểm lần lượt nằm trên các cạnh AB, AD với \(AI = \frac{1}{2}IB\) và \(AJ = \frac{2}{3}JD\). Tìm giao điểm của đường thẳng IJ với mặt phẳng (BCD).

Hướng dẫn giải

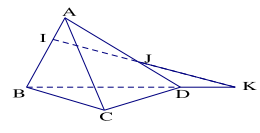
Do \(\left\{ {\begin{array}{*{20}{l}}{AI = \frac{1}{2}IB}\\{AJ = \frac{2}{3}JD}\end{array}} \right.\) nên I  kéo dài cắt BD, gọi giao điểm là K. Khi đó \(K = IJ \cap (BCD)\)

Bài 1.8. Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuôc miền trong của tam giác SCD. Tìm giao tuyến của hai mặt phẳng

a) (SBM) và (SCD)

b) (ABM) và (SCD)

c) (ABM) và (SAC)

Hướng dẫn giải

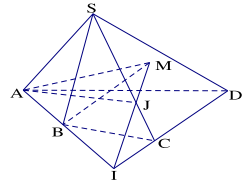
a) Ta có ngay: \((SBM) \cap (SCD) = SM\)

b) Ta có: \(M \in (ABM) \cap (SCD)\)

Trong mp (ABCD) gọi \(I = AB \cap CD\)

Suy ra: \(MI = (ABM) \cap (SCD)\)

c) Ta có: \(A \in (ABM) \cap (SAC)\).

Trong mp (SCD), gọi \(J = IM \cap SC\)

Suy ra: \(J \in (ABM) \cap (SAC)\)

Vậy: \(AJ = (ABM) \cap (SAC)\)

Bài 1.9. Cho hình chóp S.ABCD có đáy ABCD là tứ giác, M và N tương ứng là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).

Hướng dẫn giải

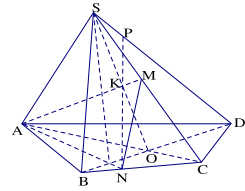
Gọi \(O = AC \cap BD\). Trong mp(SAC), gọi Trong mp (ABCD), gọi \(L = BD \cap AN\)

Chọn mặt phẳng phụ (SBD) chứa SD.

Và ta có: \(LK = (SBD) \cap (AMN)\)

Mà trong mp (SBD), có \(LK \cap SD = P\) V

ậy: \(P = SD \cap (AMN)\)

Vấn đề 3. Chứng minh ba điểm thẳng hàng

Phương pháp: Để chứng minh ba điềm thăng hàng, ta có thể chứng minh chúng cùng thuộc hai mặt phăng riêng biệt.

Bài 1.10. Cho tứ diện SABC. Trên SA, SB, SC lần lượt lấy các điểm D, E và F sao cho cắt AB tại I, E F cắt BC tại J, FD cắt CA tại K. Chứng minh rằng ba điểm I, J, K thẳng hàng.

Hướng dẫn giải

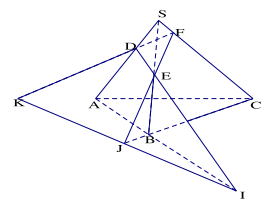
Ta có: \(\left. {\begin{array}{*{20}{l}}{I \in DE}\\{DE \subset (DEF)}\end{array}} \right\} \Rightarrow I \in (DEF)\)

và \(\left. {\begin{array}{*{20}{l}}{I \in AB}\\{AB \subset (ABC)}\end{array}} \right\} \Rightarrow I \in (ABC)\).

Suy ra: \(J \in (MNK) \cap (BCD)\)

Lí luận tương tự ta có: J, K cũng là điểm chung của hai mặt phẳng (DEF) và (ABC)

Vậy I, J, K thuộc về giao tuyến của hai mặt phẳng (DEF) và (ABC) nên I, J, K thẳng hàng.

Bài 1.11. Cho ba điểm A,B,C không thuộc mặt phẳng (Q) và các đường thẳng BC, CA,AB cắt (Q) lần lượt tại M,N,P. Chứng minh rằng M, N, P thẳng hàng.

Hướng dẫn giải

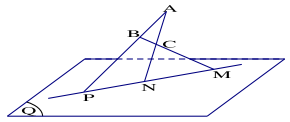
Ta có M, N, P lần lượt thuộc về hai mặt phẳng (Q) và (ABC), nên M, N, P thuộc về giao tuyến của hai mặt phẳng (Q) và (ABC). Vậy M, N, P thẳng hàng.

Bài 1.12. Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD

a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)

b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)

c) Tìm giao điểm I của đường thẳng BM và mp(SAC)

d) Tìm giao điểm P của SC và mp(ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM).

Hướng dẫn giải

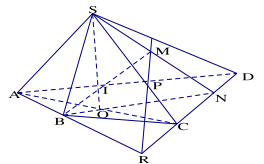
a) Gọi \(N = SM \cap CD\). Ta có \(N = CD \cap (SBM)\)

b) Gọi \(O = AC \cap BN\).Ta có: \((SBM) \cap (SAC) = SO\)

c) Gọi \(I = SO \cap BM\)

Ta có \(I = BM \cap (SAC)\)

d) Gọi \(R = AB \cap CD,P = MR \cap SC\)

Ta có \(P = SC \cap (ABM) \Rightarrow PM = (SCD) \cap (ABM)\)

Bài 1.13. Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD.

a) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)

b) Tìm giao điểm của đường thẳng BM và mp(SAC)

c) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (ABM)

Hướng dẫn giải

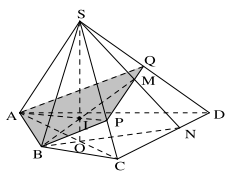
a) Gọi \({\rm{N}} = {\rm{SM}} \cap {\rm{CD}},{\rm{O}} = {\rm{AC}} \cap {\rm{BN}}\).

Khi đó \({\rm{SO}} = ({\rm{SAC}}) \cap \) (SBM).

b) Trong mp(SBM), đường thẳng BM cắt SO tại I. Ta có \({\rm{I}} = {\rm{BM}} \cap ({\rm{SAC}})\).

c) Trong mp(SAC), đường thẳng AI cắt SC tại P. Ta có P và M là hai điểm chung của mp(ABM) và mp(SCD). Vậy \(({\rm{ABM}}) \cap ({\rm{SCD}}) = {\rm{PM}}\). Đường thẳng PM cắt SD tại Q, thiết diện của hình chóp khi cắt bởi mp(ABM) là tứ giác ABPQ.

Bài 1.14. Cho hình chóp S.ABCD có đáy là hình thang ABCD(AB//CD,AB > CD) .Gọi I, J theo thứ tự là trung điểm của các cạnh SB và SC.

a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC), (SAC) và (SBD)

b) Tìm giao điểm của đường thẳng SD với mp(AIJ)

c) Xác định thiết diện của hình chóp S.ABCD cắt bởi mp(AIJ)

Hướng dẫn giải

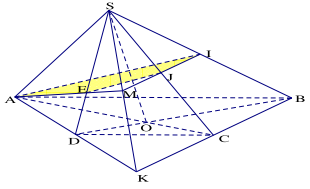
a) Gọi K là giao điểm của AD và BC, khi đó hai mătt phẳng (SAD) và (SBC) có hai điểm chung là S và K. Vậy: \((SAD) \cap (ABC) = SK\)

Gọi O là giao điểm của AC và BD. Vậy \((SAC) \cap (ABD) = SO\)

b) Gọi M là giao điểm của SK và IJ. Khi đó \((SAD) \cap (AIJ) = AM\). Gọi E là giao điểm của AM và SD thì E chính là giao điểm của SD với mp(AIJ).

c) Thiết diện của hình chóp khi cắt bởi mp(AIJ) là tứ giác AIJE.