Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Hai mặt phẳng song song Toán lớp 11, tài liệu bao gồm 4 trang, tuyển chọn 12 bài tập Hai mặt phẳng song song đầy đủ lý thuyết, phương pháp giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

A. LÝ THUYẾT CƠ BẢN

1. Vị trí tương đối của hai mặt phẳng phân biệt

Cho đường thẳng d và mặt phẳng (P). Có ba trường hợp xảy ra:

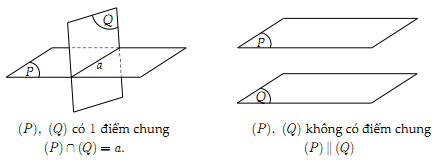
Định nghĩa. Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung.

2. Các định lí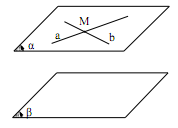

- Định lí 1. Nếu mặt $\left(\alpha \right)$ chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng $\left(\mathrm{\beta }\right)$ thì $\left(\alpha \right)$ song song với $\left(\mathrm{\beta }\right)$

Lưu ý:

- Muốn chứng minh hai mặt phẳng song song, ta phải chứng minh có hai đường thẳng cắt nhau thuộc mặt phẳng này lần lượt song song với mặt phẳng kia.

-  Muốn chứng minh đường thẳng a // (Q) ta chứng minh đường thẳng a nằm trong mặt phẳng (P) // (Q)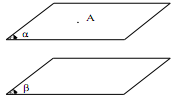

- Định lí 2. Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

Hệ quả:

- Nếu đường thẳng d song song với mặt phẳng $\left(\alpha \right)$ thì trong $\left(\alpha \right)$ có một đường thẳng song song với d và qua d có duy nhất một mặt phẳng song song với $\left(\alpha \right)$. Dó đó đường thẳng d song song với $\left(\alpha \right)$ ta phải chứng minh d thuộc mặt phẳng 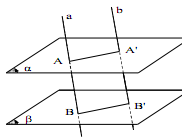$\left(\mathrm{\beta }\right)$ và có  $\left(\mathrm{\beta }\right)\left|\right|\left(\mathrm{\alpha }\right)\Rightarrow \mathrm{d}\left|\right|\left(\mathrm{\alpha }\right)$

- Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

- Cho điểm A không nằm trên mặt phẳng $\left(\alpha \right)$. Mọi đường thẳng đi qua A và song song với $\left(\alpha \right)$ đều nằm trong mặt phẳng đi qua A và song song với $\left(\alpha \right)$

- Định lí 3. Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau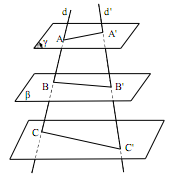

- Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.

- Định lí Thales: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.

B. BÀI TẬP

Câu 1: Cho hai đường thẳng chéo nhau a và b. (P) chứa a và song song với b, Q chưa b và song song với a. Phát biểu nào sau đây là đúng?

A. (P) và (Q) cắt nhau

B. (P) và (Q) song song với nhau

C. (P) và (Q) trùng nhau

D. (P) và (Q) cắt nhau hoặc song song với nhau.

Câu 2: Trong các mệnh đề sau, mệnh đề nào sai.

A. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.

B. Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì cắt mặt phẳng còn lại.

C. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại.

D. Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C nằm ngoài (P) lúc đó, nếu 3 đường thẳng AB, BC, CA đều cắt mặt phẳng (P) thì ba giao điểm đó thẳng hàng.

Câu 3: Cho hình bình hành ABCD. Qua các đỉnh A, B, C, D ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với mặt phẳng (ABCD). Một mặt phẳng (P) cắt bốn đường thẳng nói trên tại A’, B’, C’, D’. Hỏi A’B’C’D’ là hình gì?

A. Hình thoi

B. Hình thang có đúng một cặp cạnh song song

C. Hình chữ nhật

D. Hình bình hành

Câu 4: Cho hình lăng trụ ABC.A’B’C’. gọi I, J, K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. mặt phẳng nào sau đây song song với (IJK)?

A. (ABC)      

B. (A’BC’)

C. (BB’C’)      

D. (AA’C)

Câu 5: Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng đi qua B, C, D và song song với nhau. Mặt phẳng (∝) đi qua A và cắt Bx, Cy, Dz lần lượt tại A’, C’, D’ với BB’ = 2, DD’ = 4. Khi đó CC’ bằng:

A. 3      

B. 4      

C. 5      

D. 6

Câu 6: Cho hình lăng trụ ABC.A’B’C’. gọi I. J. K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. Mặt phẳng nào sau đây song song với (IJK)

A. (AA’B’)      

B. (AA’C’)

C. (A’B’C’)      

D. (BB’C’)

Câu 7: Cho hai đường thẳng a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q).

A. a và b là hai đường thẳng song song

B. nếu điểm M không nằm trên (P) và (Q) thì không thể coi đường thẳng nào đi qua M và cắt cả a lẫn b.

C. nếu a và b không song song với nhau, điểm M không nằm trên (P) và (Q), thì luôn có duy nhất một đường thẳng đi qua M cắt cả a và b.

D. cả 3 câu trên đều sai.

Câu 8: Khẳng định nào sau đây là đúng?

A. nếu mặt phẳng (P) chứa hai đường thẳng cùng song song với mặt phẳng (Q) thì (P) // (Q).

B. nếu hai đường thẳng cùng nằm trong một mặt phẳng lần lượt song song với hai đường thẳng của một mặt phẳng khác thì hai mặt phẳng đó song song.

C. hai mặt phẳng cùng song song với mặt phẳng thứ ba thì song song với nhau

D. cho hai mặt phẳng (P) , (Q) song song. Khi đó nếu đường thẳng a không nằm trong mặt phẳng (Q) và a song song với (P) thì a song song với (Q)

Câu 9: Trong các mệnh đề sau, những mệnh đề nào đúng?

   (1) hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.

   (2) hai mặt phẳng phân biệt không song song thì cắt nhau.

   (3) hai mặt phẳng cùng song song với một mặt phảng thứ ba thì song song với nhau.

   Một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại.

A.(1), (2)      

B. (1), (2), (3)

C. (2), (4)      

D. (1), (2), (3), (4)

Câu 10: Cho hai mặt phẳng phân biệt (P) và (Q)

   (1) nếu hai mặt phẳng (P) và (Q) song song với nhay thì mọi đường thẳng nằm trên (P) đều song song với mọi đường thẳng nằm trên (Q).

   (2) nếu mọi đường thẳng nằm trong mặt phẳng (P) đều song song với (Q) thì (P) song song với (Q).

   Trong hai phát biểu trên.

A. chỉ có một phát biểu đúng.

B. chỉ có phát biểu (2) đúng.

C. cả hai phát biểu đều đúng.

D. cả hai phát biểu đều sai.

Câu 11: Cho mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến a và b. Khi đó.

A. a và b có một điểm chúng duy nhất

B. a và b không có điểm chung nào

C. a và b trùng nhau

D. a và b song song hoặc trùng nhau