Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 121 bài tập trắc nghiệm quan hệ song song, tài liệu bao gồm 23 trang, 121 câu trắc nghiệm. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

121 bài tập trắc nghiệm quan hệ song song

Bài tập trắc nghiệm quan hệ song song

Câu 1: Cho hình chóp S.ABCD , đáy ABCD có AD cắt BC tại E. Gọi M là trung điểm của \({\rm{SA}},{\rm{N}} = {\rm{SD}} \cap ({\rm{BCM}})\). Qua điểm N kẻ đường thẳng d song song với BD. \({\rm{Khi}}\) đó d cắt:

A. \({\rm{AB}}\)

B. SC

C. SB

D. SA

Câu 2: Phát biểu nào sau đây là sai?

A. Cả 3 câu trên đều sai.

B. Hình thang có thể là hình biểu diễn của một hình bình hành.

C. Trọng tâm G của tam giác ABC có hình chiếu song song là trọng tâm \({{\rm{G}}^\prime }\) của tam giác \({{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\), trong đó \({{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\) là hình chiếu song song của tam giác ABC.

D. Hình chiếu song song của hai đường chéo nhau có thể là hai đường song song.

Câu 3: Cho tứ diện ABCD cótrọng tâm G. M,N lần lượt là trung điểm của CD,AB

. Khi đó BC và MN là hai đường thẳng:

A. chéo nhau

B. có hai điểm chung

C. song song

D. cắt nhau

Câu 4: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Điểm M thuộc cạnh SCsao cho \({\rm{SM}} = 3{\rm{MC}},{\rm{N}}\) là giao điểm của SD và (MAB). Khi đó hình chiếu song song của SM trên mp(ABC) theo phương chiếu SA là:

A. BC

B. AC

C. DB

D. DC

Câu 5: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Điểm M thuộc cạnh SC sao cho SM = 3MC,N là giao điểm của SD và (MAB). Khi đó hai đường thẳng CD và MN là hai đường thẳng:

A. cắt nhau

B. chéo nhau

C. song song

D. có hai điểm chung

Câu 6: Cho tứ diện ABCD,M là trung điểm của ABMN là trung điểm của AC,P là trung điểm của AD. Đường thẳng MN song song với mặt phẳng nào trong các mặt phẳng sau đây?

A. mặt phẳng (PCD).

B. mặt phẳng (ABC).

C. mặt phẳng (ABD).

D. mặt phẳng (BCD).

Câu 7: Cho hình chóp S.ABCD có đáy là hình bình hành. Một \(mp(\alpha )\) cắt các cạnh SA,SB,SC,SD lần lượt tại các điểm \({{\rm{A}}^\prime },{{\rm{B}}^\prime },{{\rm{C}}^\prime },{{\rm{D}}^\prime }\) sao cho tứ giác \({{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) cũng là hình bình hành. Qua S kẻ Sx,Sy lần lượt song song với AB,AD. Gọi O là giao điểm của AC và BD. Khi đó ta có:

A. Giao tuyến của \(({\rm{SAC}})\) và \(\left( {{\rm{S}}{{\rm{B}}^\prime }{{\rm{D}}^\prime }} \right)\) là đường thẳng Sx

B. Giao tuyến của \(\left( {{\rm{S}}{{\rm{B}}^\prime }{{\rm{D}}^\prime }} \right)\) và \(({\rm{SAC}})\) là đường thẳng SO

C. Giao tuyến của \(\left( {{\rm{S}}{{\rm{A}}^\prime }{{\rm{B}}^\prime }} \right)\) và \(\left( {{\rm{S}}{{\rm{C}}^\prime }{{\rm{D}}^\prime }} \right)\) là đường thẳng S

D. Giao tuyến của \(\left( {{\rm{S}}{{\rm{A}}^\prime }{{\rm{D}}^\prime }} \right)\) và \(({\rm{SBC}})\) là đường thẳng SO

Câu 8: Cho hình chóp S.ABCD. Gọi G, E lần lượt là trọng tâm các tam giác SAD và SCD . Lấy M,N\({\rm{M}},{\rm{N}}\) lần lượt là trung điểm AB,BC. Khi đó ta có:

\({\rm{A}}\). GE và MN trùng nhau

B. GE và M N chéo nhau

C. \(GE//MN\)

D. GE cắt BC

Câu 9: Cho hình chóp S.ABCD với ABCD là hình bình hành tâm O. Khi đó giao tuyến của hai mặt phẳng (SAC) và (SBD) là :

A. SC

B. SB

C. SA

D. SO

Câu 10: Trong \({\rm{mp}}(\alpha )\), Cho tứ giác ABCD có AB cắt C tại E,AC cắt B tại F,S là điểm không thuộc \((\alpha )\). Giao tuyến của (SAC) và (SBD) là:

A. SF

B. SC

C. AE

D. SE

Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình thang \(AB//CD\). Gọi d là giao tuyến của hai mf(SAB) và (SCD). Mệnh đề nào sau đây là đúng?

A. \({\rm{d}}//{\rm{AB}}\)

B. d cắt \({\rm{AB}}\)

C. \(d\) cắt \({\rm{AD}}\)

D. d cắt CD

Câu 12: Phát biểu nào sau đây là đúng?

A. Nếu 3 mặt phẳng phân biệt đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến đó hoặc đồng quy hoặc đôi một song song với nhau.

B. Nếu 3 mặt phẳng phân biệt đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến đó hoặc đồng quy .

C. Cả A, B, C đều sai.

D. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến đó hoặc đồng quy hoặc đôi một song song với nhau.

Câu 13: Cho tứ diện ABCD,M là trung điểm của cạnh CD,G là trọng tâm tứ diện. Khi đó hai đường thẳng AD và GM là hai đường thẳng:

A. chéo nhau

B. có hai điểm chung

C. song song

D. có một điểm chung

Câu 14: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất ?

A. Một điểm và một đường thẳng

B. Hai đường thẳng cắt nhau

C. Ba điểm

D. Bốn điểm

Câu 15: Cho lăng trụ tam giác \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\). Gọi M, N, P, Q lần lượt là trung điểm các cạnh \({\rm{AC}},{\rm{A}}{{\rm{A}}^\prime },{{\rm{A}}^\prime }{{\rm{C}}^\prime },{\rm{BC}}\). Khi đó:

A. (MNP) \(//\left( {{\rm{B}}{{\rm{C}}^\prime }{{\rm{A}}^\prime }} \right)\)

B. \(({\rm{MNQ}})//\left( {{{\rm{A}}^\prime }{{\rm{B}}^\prime }{\rm{C}}} \right)\)

C. \(({\rm{NQP}})//\left( {{\rm{C}}{{\rm{A}}^\prime }{{\rm{B}}^\prime }} \right)\)

D. (MNP) / / \(\left( {{{\rm{A}}^\prime }{\rm{C}}{{\rm{C}}^\prime }} \right)\)

Câu 16: Trên hình vẽ ta có hai \(mp(\alpha )\) và \((\beta )\) cắt nhau theo giao tuyến \(\Delta \). Hai đường thẳng d và \({{\rm{d}}^\prime }\) cắt các \({\rm{mp}}\) đó tại các điểm M,N và \({{\rm{M}}^\prime },{{\rm{N}}^\prime }\). Mệnh đề nào sau đây là đúng?

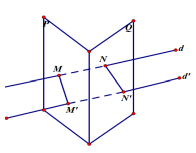
\({\rm{A}}\). d và \({{\rm{d}}^\prime }\) chéo nhau

B. d và \({{\rm{d}}^\prime }\) cắt nhau

C. d và \({d^\prime }\) song song

D. Có thể xảy ra cả 3TH

Câu 17: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai đường thẳng không có điểm chung thì song song.

B. Hai đường thẳng không cùng nằm trên một mặt phẳng thì chéo nhau.

C. Hai đường thẳng không cắt nhau thì song song.

D. Hai đường thẳng không có điểm chung thì chéo nhau.

Câu 18: Cho tứ diện ABCD. Gọi M,N là trọng tâm của tam giác ABC và ACD. Khi đó ta có:

A. MN cắt AD

B. MN//CD

C. MN cắt BC

D. \({\rm{MN}}//{\rm{BD}}\)

Câu 19: Cho hình chóp S.ABCD đáy ABCD là hình bình hành. \({\rm{Mp}}(\alpha )\) qua AB và cắt cạnh SC tại M ở giữa S và C. Khi đó : Giao tuyến của \(mp(\alpha )\) và (SCD) là:

\({\rm{A}}\). đường thẳng qua M song song với AC

B. đường thẳng qua

M song song với CD

C. MA

D. MD

Câu 20: Cho tứ diện ABCD,M là trung điểm cạnh AC,N là điểm thuộc cạnh AD sao cho \({\rm{ND}} = 2{\rm{AN}}\). O là một điểm thuộc miền trong của tam giác BCD. Khi đó AB và MN là hai đường thẳng:

A. có hai điểm chung

B. song song

C. cắt nhau

D. chéo nhau

Câu 21: Cho hình chóp SABCD. Đáy ABCD là hình bình hành. Giả sử M thuộc đoạn SB.Mặt phẳng (ADM) cắt hình chóp SABCD theo thiết diện là hình:

A. Hình bình hành.

B. Tam giác.

C. Hình thang.

D. Hình chữ nhật.

Câu 22: Trong \({\rm{mp}}(\alpha )\), Cho tứ giác ABCD có AB cắt C tại E,AC cắt B tại F,S là điểm không thuộc \((\alpha )\). Giao tuyến của (SAB) và (SCD) là:

A. CD

B. SD

C. AC

D. SE

Câu 23: Cho hình chóp A.ABCD, đáy ABCD có AD cắt BC tại E. Gọi M là trung điểm của \({\rm{SA}},{\rm{N}} = {\rm{SD}} \cap ({\rm{BCM}})\). Khi đó ba đường thẳng nào đồng quy?

A. MN,DC,AB

B. NB,MC,AD

C. \({\rm{MN}},{\rm{AD}},{\rm{BC}}\)

D. AD, SC, BN

Câu 24: Trong các mệnh đề sau mệnh đề nào sai :

A. Dùng nét đứt để biểu diễn cho đường bị che khuất

B. Hình biểu diễn của đường thẳng là đường thẳng

C. Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.

D. Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song nhau

Câu 25: Tìm mệnh đề đúng?

A. Nếu hai mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau thì mọi đường thẳng nằm trong mặt phẳng \((\alpha )\) đều song song với \((\beta )\).

B. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt \((\alpha )\) và \((\beta )\) thì \((\alpha )\) song song với \((\beta )\).

C. Nếu hai mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau thì mọi đường thẳng nằm trong mặt phẳng \((\alpha )\) đều song song với mọi đường thẳng nằm trong \((\beta )\).

D. Qua 1 điểm nằm ngoài mặt phẳng cho trước ta vẽ được 1 và chỉ 1 đường thẳng song song với mặt phẳng trước đó.

Bài 26: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M là trung điểm của SA. Thiết diện của mặt phẳng (MCD) với hình chóp S.ABCD là hình gì?

   A. tam giác      B. hình bình hành

   C. hình thang      D. hình thoi

Đáp án: C

   Vì CD ⊂ (MCD), CD // AB, AB ⊂ (SAB) nên giao tuyến của (MCD) và (SAB) là đường thẳng qua M và song song với AB, cắt SB tại N là trung điểm của SB. Vậy MN // CD. Hơn nữa MN ≠ CD. Vậy thiết diện là hình thang CNMD.

Bài 27: Cho hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng, có tâm lần lượt là O và O’. Chọn khẳng định đúng trong các khẳng định sau:

   A. OO’ // (ABCD)      B. OO’ // (ABEF)

   C. OO’ // (BDF)      D. OO’ / /(ADF)

Đáp án: D

Bài 28: Cho tứ diện ABCD. Hai điểm M, N lần lượt là trung điểm của AC, AD. Mặt phẳng (∝) chứa MN và song song với AB. Thiết diện của (∝) với tứ diện ABCD là:

   A. hình thang      B. hình bình hành

   C. hình chữ nhật      D. hình vuông