Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các công thức tính diện tích, chu vi hình tam giác Toán lớp 10, tài liệu bao gồm 1 trang, tổng hợp đầy đủ lí thuyết công thức tính diện tích tam giác, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

CÁC CÔNG THỨC TÍNH DIỆN TÍCH, CHU VI HÌNH TAM GIÁC

A. Công thức tính chu vi, diện tích hình tam giác

1. Công thức tính chu vi hình tam giác

Cho tam giác ABC với độ dài 3 cạnh là BC = a; AC = b; AB = c và chiều cao ứng với cạnh a là h.

Chu vi tam giác là tổng độ dài ba cạnh của tam giác:

C = a + b + c (đơn vị độ dài)

2. Công thức tính diện tích hình tam giác

Diện tích tam giác bằng một nửa tích của cạnh đáy nhân với chiều cao tương ứng.

S = $\frac{1}{2}$a . h (đơn vị diện tích)

* Đối với tam giác thường:

S = $\frac{1}{2}$a . h (đơn vị diện tích)

* Đối với tam giác vuông:

Ngoài công thức tính diện tích tam giác như tam giác thường, để tính diện tích tam giác vuông ta có thể tính bằng cách lấy tích hai cạnh góc vuông rồi chia cho 2.

S = $\frac{1}{2}$a . h = $\frac{1}{2}$b. c (đơn vị diện tích)

*Công thức tính diện tích tam giác cân

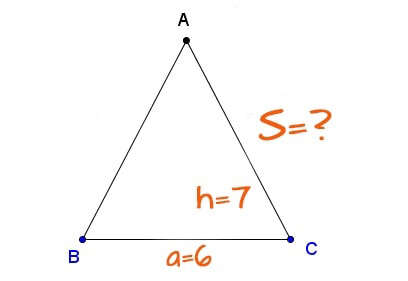
Công thức tính diện tích tam giác cân:

+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)

+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).

8 công thức tính diện tích tam giác nâng cao

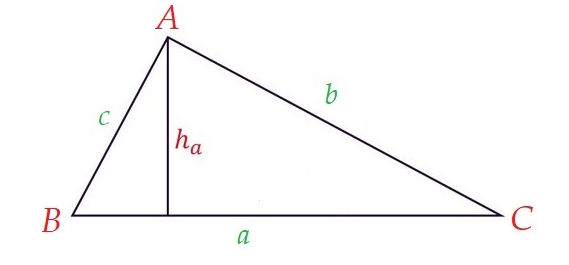
Cho tam giác ABC, ta kí hiệu độ dài các cạnh là a=BC, b=CA, c=AB, các góc của tam giác được viết đơn giản là A,B,C. Diện tích tam giác được kí hiệu là S.

Công thức 1

Gọi độ dài đường cao (chiều cao) hạ từ các đỉnh A,B,C lần lượt là h_a, h_b, h_c.

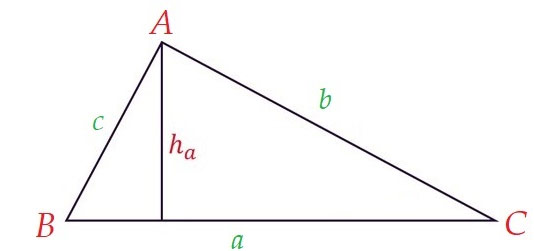
Đặc biệt:

Diện tích tam giác vuông tại A là: 

Diện tích tam giác cân tại A là:  (với H là trung điểm của BC).

Diện tích tam giác đều cạnh a là: 

Công thức 2

Công thức 3

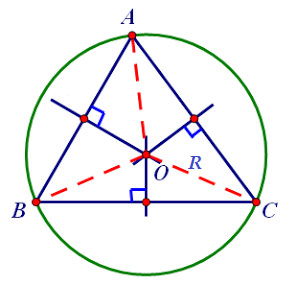
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Ta có: 

Công thức 4

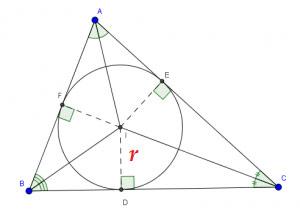
Gọi r là bán kính đường tròn nội tiếp tam giác ABC và p là nửa chu vi tam giác (): 

Công thức 5 (Công thức Héron)

Với p là kí hiệu nửa chu vi như ở mục 4, ta có:  

Công thức 6

Công thức 7

Trong mặt phẳng Oxy, gọi tọa độ các đỉnh của tam giác ABC là: A(x_A,y_A),B(x_B,y_B),C(x_C,y_C).
Khi đó: 

Công thức 8

Áp dụng trong không gian, với khái niệm tích có hướng của 2 vectơ. Ta có: 

B. Ví dụ minh họa

Ví dụ 1. Cho hình vẽ sau:

Tính diện tích phần hình được tô màu. (coi mỗi cạnh của 1 ô vuông nhỏ là 1dm)

Hướng dẫn giải:

Ta chia hình ban đầu thành hai hình: Hình vuông ABCF và hình tam giác DFE

Diện tích hình vông ABCF là:

S_ABFC = 2.2 = 4 (dm²).

Diện tích tam giác DEF là:

S_DEF = $\frac{1}{2}$2.1 = 1 (dm²).

Vậy diện tích hình được tô màu là:

4 + 1 = 5 (dm²).

Ví dụ 2. Tính diện tích tam giác biết chiều cao của tam giác đó là 5cm và độ dài cạnh đáy tương ứng là 8cm.

Hướng dẫn giải:

Diện tích tam giác là:

S = $\frac{1}{2}.5.8=20\left(c{m}^2\right)$

Vậy diện tích tam giác là 20cm².

Ví dụ 3. Cho tam giác ABC vuông tại A có các cạnh AB = 3cm; AC = 4cm và BC = 5cm. Tính chu vi và diện tích tam giác ABC.

Hướng dẫn giải:

Chu vi tam giác ABC là:

3 + 4 + 5 = 12 (cm)

Diện tích tam giác ABC là:

S = $\frac{1}{2}.3.4=6\left(c{m}^2\right)$

Vậy chu vi tam giác ABC là 12cm, diện tích tam giác ABC là 6cm².

C. Bài tập tự luyện

Bài 1. Tính diện tích tam giác có:

a) Độ dài cạnh đáy là 15cm và chiều cao là 12cm.

b) Độ dài đáy là 6cm và chiều cao là 4,5cm.

Bài 2. Tính diện tích tam giác vuông có:

a) Hai cạnh góc vuông lần lượt là 3cm và 4cm.

b) Hai cạnh góc vuông lần lượt là 6m và 8m.

Bài 3. Cho tam giác ABC đều có cạnh bằng 12 cm. Chiều cao của tam giác là 14cm. Tính chu vi, diện tích tam giác.

Bài 4. Cho hình chữ nhật ABCD có AD = 4cm, AB = 6cm. DM = 3cm, MC = 1cm.

a) Tính diện tích tam giác ADM?

b) Tính diện tích tam giác AMC?

Bài 5. Tính diện tích phần được tô màu trong hình vẽ: