Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 8 Bài 1: Liên hệ giữa thứ tự và phép cộng chọn lọc, có đáp án. Tài liệu gồm 22 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 8. Hi vọng với bộ câu hỏi trắc nghiệm Liên hệ giữa thứ tự và phép cộng có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi môn Toán 8.
Giới thiệu về tài liệu:
- Số câu hỏi trắc nghiệm: 22 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Liên hệ giữa thứ tự và phép cộng có đáp án - Toán lớp 8:
Trắc nghiệm Toán 8
Bài 1: Liên hệ giữa thứ tự và phép cộng
Bài 1: Cho biết a < b. Trong các khẳng định sau, số khẳng định sai là?
(I) a - 1 < b - 1
(II) a - 1 < b
(III) a + 2 < b + 1
A. 1
B. 2
C. 3
D. 0
Lời giải
+ Vì a < b, cộng hai vế của bất đẳng thức với -1 ta được a - 1 < b - 1 ⇒ (I) đúng.
+ Vì a - 1 < b - 1 (cmt) mà b - 1 < b nên a - 1 < b ⇒ (II) đúng
+ Vì a < b, cộng hai vế của bất đẳng thức với 1 ta được a + 1 < b + 1 mà
a + 1 < a + 2 nên ta chưa đủ dữ kiện để nói rằng a + 2 < b + 1 ⇒ (III) sai.
Vậy có 1 khẳng định sai.
Đáp án cần chọn là: A
Bài 2: Cho biết a < b. Trong các khẳng định sau, số khẳng định đúng là?
(I) a - 1 < b - 1 (II) a - 1 < b (III) a + 2 < b + 1
A. 1
B. 2
C. 3
D. 0
Lời giải
+ Vì a < b, cộng hai vế của bất đẳng thức với -1 ta được: a - 1 < b - 1 ⇒ (I) đúng.
+ Vì a - 1 < b - 1 (cmt) mà b - 1 < b nên a - 1 < b ⇒ (II) đúng.
+ Vì a < b, cộng hai vế của bất đẳng thức với 1 ta được: a + 1 < b + 1 mà
a + 1 < a + 2 nên ta chưa đủ dữ kiện để nói rằng a + 2 < b + 1 ⇒ (III) sai.
Do đó có 2 khẳng định đúng.
Đáp án cần chọn là: B
Bài 3: Cho a bất kỳ, chọn câu sai?
A. 2a - 5 < 2a + 1
B. 3a - 3 > 3a - 1
C. 4a < 4a + 1
D. 5a + 1 > 5a - 2
Lời giải
+ Vì -5 < 1 nên cộng hai vế của bất đẳng thức với số 2a bất kì ta được
2a - 5 < 2a + 1 ⇒ A đúng.
+ Vì 0 < 1 nên cộng hai vế của bất đẳng thức với số 4a bất kì ta được
4a < 4a + 1 ⇒ C đúng.
+ Vì 1 > -2 nên cộng hai vế của bất đẳng thức với số 5a bất kì ta được
5a + 1 < 5a - 2 ⇒ D đúng.
+ Vì -3 < -1 nên cộng hai vế của bất đẳng thức với số 3a bất kì ta được
3a - 3 < 3a - 1 ⇒ B sai.
Đáp án cần chọn là: B
Bài 4: Cho a bất kỳ, chọn câu sai?
A. -2a - 5 < -2a + 1
B. 3a - 3 < 3a - 1
C. 4a < 4a + 1
D. -5a + 1 < -5a - 2
Lời giải
+ Vì -5 < 1 nên cộng hai vế của bất đẳng thức với số -2a bất kì ta được:
-2a - 5 < -2a + 1 ⇒ A đúng.
+ Vì 0 < 1 nên cộng hai vế của bất đẳng thức với số 4a bất kì ta được:
4a < 4a + 1 ⇒ C đúng.
+ Vì 1 > -2 nên cộng hai vế của bất đẳng thức với số -5a bất kì ta được:
-5a + 1 > -5a - 2 ⇒ D sai.
+ Vì -3 < -1 nên cộng hai vế của bất đẳng thức với số 3a bất kì ta được:
3a - 3 < 3a - 1 ⇒ B đúng.
Đáp án cần chọn là: D
Bài 5: Cho x - 3 ≤ y - 3, so sánh x và y. Chọn đáp án đúng nhất?
A. x < y
B. x = y
C. x > y
D. x ≤ y
Lời giải
Cộng cả hai vế của bất đẳng thức x - 3 ≤ y - 3 với 3 ta được:
x - 3 ≤ y - 3 ⇒ x - 3 + 3 ≤ y - 3 + 3 ⇒ x ≤ y.
Đáp án cần chọn là: D
Bài 6: Cho a - 3 < b. So sánh a + 10 và b + 13?
A. a + 10 < b + 13
B. a + 10 > b + 13
C. a + 10 = b + 13
D. Không đủ dữ kiện để so sánh
Lời giải
Cộng cả hai vế của bất đẳng thức a - 3 < b với 13 ta được:
a - 3 < b ⇒ a - 3 + 13 < b + 13 ⇒ a + 10 < b + 13.
Đáp án cần chọn là: A
Bài 7: Cho biết a - 1 = b + 2 = c - 3. Hãy sắp xếp các số a, b, c theo thứ tự tăng dần?
A. b < c < a
B. a < b < c
C. b < a < c
D. a < c < b
Lời giải
Từ a - 1 = b + 2 suy ra a = b + 2 + 1 = b + 3.
Từ b + 2 = c - 3 suy ra c = b + 2 + 3 = b + 5.
Mà b < b + 3 < b + 5 nên b < a < c.
Đáp án cần chọn là: C
Bài 8: Cho biết a = b - 1 = c - 3. Hãy sắp xếp các số a, b, c theo thứ tự tăng dần?
A. b < c < a
B. a < b < c
C. b < a < c
D. a < c < b
Lời giải
Từ a = b - 1 suy ra b = a + 1.
Từ a = c - 3 suy ra c = a + 3.
Mà a < a + 1 < a + 3 nên a < b < c.
Đáp án cần chọn là: B
Bài 9: Với a, b, c bất kỳ. Hãy so sánh 3(a2 + b2 + c2) và (a + b + c)2
A. 3(a2 + b2 + c2) = (a + b + c)2
B. 3(a2 + b2 + c2) ≤ (a + b + c)2
C. 3(a2 + b2 + c2) ≥ (a + b + c)2
D. 3(a2 + b2 + c2) < (a + b + c)2
Lời giải
Xét hiệu:
3(a2 + b2 + c2) - (a + b + c)2
= 3a2 + 3b2 + 3c2 - a2 - b2 - c2 - 2ab - 2bc - 2ac
= 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac
= (a - b)2 + (b - c)2 + (c - a)2 ≥ 0
(vì (a - b)2 ≥ 0; (b - c)2 ≥ 0; (c - a)2 ≥ 0 với mọi a, b, c
Nên 3(a2 + b2 + c2) ≥ (a + b + c)2.
Đáp án cần chọn là: C
Bài 10: Với a, b, c bất kỳ. Hãy so sánh a2 + b2 + c2 và ab + bc + ca?
A. a2 + b2 + c2 = ab + bc + ca
B. a2 + b2 + c2 ≥ ab + bc + ca
C. a2 + b2 + c2 ≤ ab + bc + ca
D. a2 + b2 + c2 > ab + bc + ca\
Lời giải
Xét hiệu:
a2 + b2 + c2 - ab - bc - ca
= 
(2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca)
= [(a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ca + a2)]
= [(a - b)2 + (b - c)2 + (c - a)2] ≥ 0
(vì (a - b)2 ≥ 0; (b - c)2 ≥ 0; (c - a)2 ≥ 0 với mọi a, b, c)
Nên a2 + b2 + c2 ≥ ab + bc + ca.
Dấu “=” xảy ra khi a = b = c.
Đáp án cần chọn là: B
Bài 11: Cho a > b khi đó
A. a - b > 0
B. a - b < 0
C. a - b = 0
D. a - b ≤ 0
Lời giải
Từ a > b, cộng -b vào hai vế ta được a - b > b - b, tức là a - b > 0.
Đáp án cần chọn là: A
Bài 12: So sánh m và n biết m - = n?
A. m < n
B. m = n
C. m ≤ n
D. m > n
Lời giải
Ta có: m - = n ⇒ m - n = ⇒ m - n > 0 ⇒ m > n.
Đáp án cần chọn là: D
Bài 13: So sánh m và n biết m + = n?
A. m < n
B. m = n
C. m > n
D. Cả A, B, C đều đúng
Lời giải
Ta có: m + = n ⇒ m - n = - ⇒ m - n < 0 ⇒ m < n.
Đáp án cần chọn là: A
Bài 14: Cho a + 8 < b. So sánh a - 7 và b - 15?
A. a - 7 < b - 15
B. a - 7 > b - 15
C. a - 7 ≥ b - 15
D. a - 7 ≤ b - 15
Lời giải
Cộng cả hai vế của bất đẳng thức a + 8 < b với (-15) ta được
a + 8 < b ⇒ a + 8 - 15 < b - 15 ⇒ a - 7 < b - 15
Đáp án cần chọn là: A
Bài 15: Cho a - 3 < b. So sánh a + 10 và b + 13?
A. a + 10 < b + 13
B. a + 10 > b + 13
C. a + 10 = b + 13
D. Không đủ dữ kiện để so sánh
Lời giải
Cộng cả hai vế của bất đẳng thức a - 3 < b với 13 ta được:
a - 3 < b ⇒ a - 3 + 13 < b + 13 ⇒ a + 10 < b + 13.
Đáp án cần chọn là: A
Bài 16: Cho biết a - 1 = b + 2 = c - 3. Hãy sắp xếp các số a, b, c theo thứ tự tăng dần?
A. b < c < a
B. a < b < c
C. b < a < c
D. a < c < b
Lời giải
Từ a - 1 = b + 2 suy ra a = b + 2 + 1 = b + 3.
Từ b + 2 = c - 3 suy ra c = b + 2 + 3 = b + 5.
Mà b < b + 3 < b + 5 nên b < a < c.
Đáp án cần chọn là: C
Bài 17: Cho biết a = b - 1 = c - 3. Hãy sắp xếp các số a, b, c theo thứ tự tăng dần?
A. b < c < a
B. a < b < c
C. b < a < c
D. a < c < b
Lời giải
Từ a = b - 1 suy ra b = a + 1.
Từ a = c - 3 suy ra c = a + 3.
Mà a < a + 1 < a + 3 nên a < b < c.
Đáp án cần chọn là: B
Bài 18: Với a, b, c bất kỳ. Hãy so sánh 3(a2 + b2 + c2) và (a + b + c)2
A. 3(a2 + b2 + c2) = (a + b + c)2
B. 3(a2 + b2 + c2) ≤ (a + b + c)2
C. 3(a2 + b2 + c2) ≥ (a + b + c)2
D. 3(a2 + b2 + c2) < (a + b + c)2
Lời giải
Xét hiệu:
3(a2 + b2 + c2) - (a + b + c)2
= 3a2 + 3b2 + 3c2 - a2 - b2 - c2 - 2ab - 2bc - 2ac
= 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac
= (a - b)2 + (b - c)2 + (c - a)2 ≥ 0
(vì (a - b)2 ≥ 0; (b - c)2 ≥ 0; (c - a)2 ≥ 0 với mọi a, b, c
Nên 3(a2 + b2 + c2) ≥ (a + b + c)2.
Đáp án cần chọn là: C
Bài 19: Với a, b, c bất kỳ. Hãy so sánh a2 + b2 + c2 và ab + bc + ca?
A. a2 + b2 + c2 = ab + bc + ca
B. a2 + b2 + c2 ≥ ab + bc + ca
C. a2 + b2 + c2 ≤ ab + bc + ca
D. a2 + b2 + c2 > ab + bc + ca
Lời giải
Xét hiệu:
a2 + b2 + c2 - ab - bc - ca
= (2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca)
= [(a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ca + a2)]
= [(a - b)2 + (b - c)2 + (c - a)2] ≥ 0
(vì (a - b)2 ≥ 0; (b - c)2 ≥ 0; (c - a)2 ≥ 0 với mọi a, b, c)
Nên a2 + b2 + c2 ≥ ab + bc + ca.
Dấu “=” xảy ra khi a = b = c.
Đáp án cần chọn là: B
Bài 20: Với a, b bất kỳ. Chọn khẳng định sai?
A. a2 + 5 > 4a
B. a2 + 10 < 6a - 1
C. a2 + 1 > a
D. ab - b2 ≤ a2
Lời giải
* a2 + 5 - 4a = a2 - 4a + 4 + 1 = (a - 2)2 + 1 > 0 (luôn đúng) nên a2 + 5 > 4a
* a2 + 1 - a = a2 - 2a.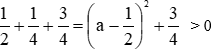
(luôn đúng) nên a2 + 1 > a
a2 + 10 - (6a + 1)
= a2 - 6a + 10 - 1
= a2 - 6a + 9
= (a - 3)2 ≥ 0
Vì (a - 3)2 ≥ 0 (luôn đúng) nên a2 + 10 > 6a + 1. Do đó B sai.
* Ta có:
Vì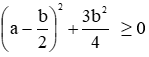 
(luôn đúng) nên a2 ≥ ab - b2.
Đáp án cần chọn là: B
Bài 21: Với a, b bất kỳ. Chọn khẳng định sai?
A. a2 + 3 > -2a
B. 4a + 4 ≤ a2 + 8
C. a2 + 1 < a
D. ab - b2 ≤ a2
Lời giải
* a2 + 3 + 2a = a2 + 2a + 1 + 2 = (a + 1)2 + 2 > 0 (luôn đúng) nên a2 + 3 > -2a nên A đúng.
* a2 + 8 - 4a - 4 = a2 - 4a + 4 = (a - 2)2 ≥ 0 (luôn đúng) nên a2 + 8 ≥ 4a + 4 hay 4a + 4 ≤ a2 + 8 nên B đúng.
* a2 + 1 - a = a2 - 2a.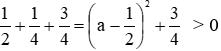
(luôn đúng) nên a2 + 1 > a hay C sai.
* Ta có:
Vì 
(luôn đúng) nên a2 ≥ ab - b2 hay D đúng.
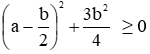
Đáp án cần chọn là: C
Bài 22: Cho a > 1 > b, chọn khẳng định không đúng?
A. a -1 > 0
B. a - b < 0
C. 1 - b > 0
D. a - b > 0
Lời giải
Từ a > b, cộng -b vào hai vế ta được a - b > b - b, tức là a - b > 0.
Do đó D đúng, B sai.
Ngoài ra A, C đúng vì:
Cộng cả hai vế của bất đẳng thức a > 1 với (-1) ta được:
a + (-1) > 1 + (-1) hay a - 1 > 0.
Cộng cả hai vế của bất đẳng thức 1 > b với -b ta được:
1 + (-b) > b + (-b) hay 1 - b > 0.
Đáp án cần chọn là: B
Bài giảng Toán 8 Bài 1 : Liên hệ giữa thứ tự và phép cộng
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
