Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 8 Bài 5: Phương trình chứa dấu giá trị tuyệt đối chọn lọc, có đáp án. Tài liệu gồm 28 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 8. Hi vọng với bộ câu hỏi trắc nghiệm Phương trình chứa dấu giá trị tuyệt đối có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi môn Toán 8.
Giới thiệu về tài liệu:
- Số câu hỏi trắc nghiệm: 28 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Phương trình chứa dấu giá trị tuyệt đối có đáp án - Toán lớp 8:

Trắc nghiệm Toán 8
Bài 5: Phương trình chứa dấu giá trị tuyệt đối
Bài 1: Tập nghiệm của phương trình |5x – 3| = x + 7 là
Lời giải
TH1: |5x – 3| = 5x – 3 nếu |5x – 3| ≥ 0 ⇔ 5x ≥ 3 ⇔ x ≥
Phương trình đã cho trở thành 5x – 3 = x + 7
⇔ 4x = 10 ⇔ x = 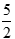
TH2: |5x – 3| = -(5x – 3) nếu 5x – 3 < 0 ⇔ 5x < 3 ⇔ x <
Phương trình đã cho trở thành –(5x – 3) = x + 7
⇔ -6x = 4 ⇔ x = 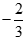
Vậy tập nghiệm của phương trình S =
Đáp án cần chọn là: D
Bài 2: Tập nghiệm của phương trình - |5x – 3| = x + 7 là
Lời giải
TH1: |5x – 3| = 5x – 3 nếu |5x – 3| ≥ 0 ⇔ 5x ≥ 3 ⇔ x ≥
Phương trình đã cho trở thành –(5x – 3) = x + 7
⇔ -6x = 4 ⇔ x = 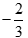
TH2: |5x – 3| = -(5x – 3) nếu 5x – 3 < 0 ⇔ 5x < 3 ⇔ x <
Phương trình đã cho trở thành –[- (5x – 3)] = x + 7
⇔ 5x – 3 = x + 7
⇔ 4x = 10 ⇔ x = 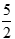
Vậy tập nghiệm của phương trình S = Ø
Đáp án cần chọn là: A
Bài 3: Số nghiệm của phương trình |x – 3|+ 3x = 7 là
A. 3
B. 2
C. 0
D. 1
Lời giải
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ⇔ x ≥ 3
Phương trình đã cho trở thành x – 3 + 3x = 7
⇔ 4x = 10 ⇔ x = 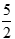
TH2: |x – 3| = -(x – 3) khi x – 3< 0 ⇔ x < 3
Phương trình đã cho trở thành –(x – 3) + 3x = 7
⇔2x = 4 ⇔ x = 2 (TM)
Vậy phương trình có một nghiệm x = 2
Đáp án cần chọn là: D
Bài 4: Số nghiệm của phương trình 2|x – 3| + x = 3 là:
A. 1
B. 2
C. 0
D. 3
Lời giải
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ⇔ x ≥ 3
Phương trình đã cho trở thành 2(x – 3) + x = 3
⇔ 2x – 6 + x – 3 = 0
⇔ 3x – 9 = 0 ⇔ x = 3 (TM)
TH2: |x – 3| = -(x – 3) khi x – 3< 0 ⇔ x < 3
Phương trình đã cho trở thành -2(x – 3) + x = 3
⇔-x = -3 ⇔ x = 3 (TM)
Vậy phương trình có một nghiệm x = 3
Đáp án cần chọn là: A
Bài 5: Phương trình nào sau đây vô nghiệm?
A. |x – 1| = 1
B. |x| = -9
C. |x + 3| = 0
D. |2x| = 10
Lời giải
+) Xét |x – 1| = 1
TH1: |x – 1| = x – 1 khi x ≥ 1, nên ta có phương trình x – 1 = 1 ⇔ x = 2 (TM)
TH2: |x – 1| = 1 – x khi x < 1 nên ta có phương trình 1 – x = 1 ⇔ x = 0 (TM)
Vậy S = {0; 2}
+) Xét |x + 3| = 0 ⇔ x + 3 = 0 ⇒ x = -3 nên S = {-3}
+) Xét |2x| = 10
TH1: |2x| = 2x khi x ≥ 0 nên ta có phương trình 2x = 10 ⇒ x = 5 (TM)
TH2: |2x| = -2x khi x < 0 nên ta có phương trình -2x = 10 ⇔ x = -5 (TM)
Vậy S = {5; -5}
+) Xét |x| = -9
Thấy rằng |x| ≥ 0; Ɐx mà -9 < 0 nên |x| > -9 với mọi x. Hay phương trình |x| = -9 vô nghiệm.
Đáp án cần chọn là: B
Bài 6: Tổng các nghiệm của phương trình |3x – 1| = x + 4 là
Lời giải
TH1: |3x – 1| = 3x – 1 khi |3x – 1| ≥ 0 ⇔ 3x ≥ 1 ⇔ x ≥
Phương trình đã cho trở thành 3x – 1 = x + 4
⇔ 2x = 5 ⇔ x = 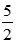
TH2: |3x – 1| = 1 – 3x khi 3x – 1 < 0 ⇔ x <
Phương trình đã cho trở thành 1 – 3x = x + 4
Đáp án cần chọn là: D
Bài 7: Số nghiệm của phương trình |3x – 1| = 3x – 1 là
A. 1
B. 2
C. 0
D. Vô số
Lời giải
Nếu 3x – 1 ≥ 0 ⇔ 3x ≥ 1 ⇔ x ≥ 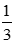
Khi đó phương trình trở thành 3x – 1 = 3x – 1 ⇔ 0x = 0 (đúng)
Nên x ≥ 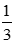
Nếu 3x – 1 < 0 ⇔ 3x < 1 ⇔ x < 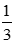
Khi đó phương trình trở thành 3x – 1 = 1 – 3x ⇔ 2 = 6x ⇔ x = 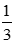
Do đó phương trình có nghiệm x ≥ 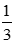
Đáp án cần chọn là: D
Bài 8: Nghiệm lớn nhất của phương trình |2x| = 3 – 3x là
Lời giải
TH1: |2x| = 2x khi 2x ≥ 0 ⇔ x ≥ 0
Phương trình đã cho trở thành 2x = 3 – 3x ⇔ 5x = 3 ⇔ x = 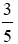
TH2: |2x| = -2x khi 2x < 0 ⇔ x < 0
Phương trình đã cho trở thành -2x = 3 – 3x ⇔ x = 3 (KTM)
Vậy phương trình có nghiệm x =
Đáp án cần chọn là: C
Bài 9: Nghiệm lớn nhất của phương trình 5 - |2x| = -3x là:
A. -5
B. -1
C. 0
D. 5
Lời giải
TH1: |2x| = 2x khi 2x ≥ 0 ⇔ x ≥ 0
Phương trình đã cho trở thành 5 – 2x = -3x ⇔ 5 = -3x + 2x
⇔ x = -5 (KTM)
TH2: |2x| = -2x khi 2x < 0 ⇔ x < 0
Phương trình đã cho trở thành 5 + 2x = -3x ⇔ 5 = -5x ⇔ x = -1 (TM)
Vậy phương trình có nghiệm duy nhất x = -1
Đáp án cần chọn là: B
Bài 10: Số nghiệm của phương trình |1 – x| - |2x – 1| = x – 2 là
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta có |1 – x| - |2x – 1| = x – 2 (1)
Xét:
Ta có bảng xét dấu đa thức 1 – x và 2x – 1 dưới đây
Từ bảng xét dấu ta có:
TH1: x < 
1 – x – (1 – 2x) = x – 2 ⇔ 1 – x – 1 + 2x = x – 2 ⇔ x = x – 2
⇔ 0 = - 2 (vô lý)
TH2: 
TH3: x > 1, khi đó |2x – 1| = 2x – 1; |1 – x| = x – 1 nên phương trình (1) trở thành
x – 1 – (2x – 1) = x – 2 ⇔ -x + 1 = x – 2 ⇔ 2x = 3 ⇔ x = 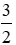
vậy phương trình có hai nghiệm x = 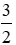
Đáp án cần chọn là: B
Bài 11: Cho các khẳng định sau:
(1) |x – 3| = 1 chỉ có một nghiệm là x = 2
(2) x = 4 là nghiệm của phương trình |x – 3| = 1
(3) |x – 3| = 1 có hai nghiệm là x = 2 và x = 4
Các khẳng định đúng là:
A. (1); (3)
B. (2); (3)
C. Chỉ (3)
D. Chỉ (2)
Lời giải
Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ⇔ x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ⇔ x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ⇔ x < 3
Phương trình đã cho trở thanh 3 – x = 1 ⇔ x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4
Nên x = 4 là nghiệm của phương trình |x – 3| = 1
Khẳng định đúng là (2) và (3)
Đáp án cần chọn là: B
Bài 12: Cho các khẳng định sau:
(1) Phương trình |x – 3| = 1 chỉ có một nghiệm là x = 2
(2) Phương trình |x – 1| = 0 có 2 nghiệm phân biệt
(3) Phương trình |x – 3| = 1 có hai nghiệm phân biệt là x = 2 và x = 4
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3
Lời giải
Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ⇔ x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ⇔ x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ⇔ x < 3
Phương trình đã cho trở thanh 3 – x = 1 ⇔ x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4 hay (1) sai và (3) đúng
|x – 1| = 0 ⇔ x – 1 = 0 ⇔ x = 1 nên phương trình |x – 1| = 0 có nghiệm duy nhất hay (2) sai.
Vậy có 1 khẳng định đúng
Đáp án cần chọn là: B
Bài 13: Nghiệm nhỏ nhất của phương trình |2 + 3x| = |4x – 3| là
Lời giải
Ta có |2 + 3x| = |4x – 3|
Vậy nghiệm nhỏ nhất của phương trình là x =
Đáp án cần chọn là: A
Bài 14: Nghiệm nhỏ nhất của phương trình |5 – 2x| = |x – 1| là:
A. 2
B. 5
C. -2
D. 4
Lời giải
Ta có |5 – 2x| = |x – 1|
Vậy nghiệm nhỏ nhất của phương trình là x = 2
Đáp án cần chọn là: A
Bài 15: Tổng các nghiệm của phương trình |3x – 1| = x + 4 là
Lời giải
TH1: |3x – 1| = 3x – 1 khi |3x – 1| ≥ 0 ⇔ 3x ≥ 1 ⇔ x ≥
Phương trình đã cho trở thành 3x – 1 = x + 4
⇔ 2x = 5 ⇔ x = 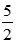
TH2: |3x – 1| = 1 – 3x khi 3x – 1 < 0 ⇔ x <
Phương trình đã cho trở thành 1 – 3x = x + 4
Đáp án cần chọn là: D
Bài 16: Số nghiệm của phương trình |3x – 1| = 3x – 1 là
A. 1
B. 2
C. 0
D. Vô số
Lời giải
Nếu 3x – 1 ≥ 0 ⇔ 3x ≥ 1 ⇔ x ≥ 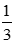
Khi đó phương trình trở thành 3x – 1 = 3x – 1 ⇔ 0x = 0 (đúng)
Nên x ≥ 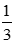
Nếu 3x – 1 < 0 ⇔ 3x < 1 ⇔ x < 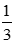
Khi đó phương trình trở thành 3x – 1 = 1 – 3x ⇔ 2 = 6x ⇔ x = 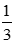
Do đó phương trình có nghiệm x ≥ 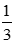
Đáp án cần chọn là: D
Bài 17: Nghiệm lớn nhất của phương trình |2x| = 3 – 3x là
Lời giải
TH1: |2x| = 2x khi 2x ≥ 0 ⇔ x ≥ 0
Phương trình đã cho trở thành 2x = 3 – 3x ⇔ 5x = 3 ⇔ x = 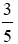
TH2: |2x| = -2x khi 2x < 0 ⇔ x < 0
Phương trình đã cho trở thành -2x = 3 – 3x ⇔ x = 3 (KTM)
Vậy phương trình có nghiệm x =
Đáp án cần chọn là: C
Bài 18: Nghiệm lớn nhất của phương trình 5 - |2x| = -3x là:
A. -5
B. -1
C. 0
D. 5
Lời giải
TH1: |2x| = 2x khi 2x ≥ 0 ⇔ x ≥ 0
Phương trình đã cho trở thành 5 – 2x = -3x ⇔ 5 = -3x + 2x
⇔ x = -5 (KTM)
TH2: |2x| = -2x khi 2x < 0 ⇔ x < 0
Phương trình đã cho trở thành 5 + 2x = -3x ⇔ 5 = -5x ⇔ x = -1 (TM)
Vậy phương trình có nghiệm duy nhất x = -1
Đáp án cần chọn là: B
Bài 19: Số nghiệm của phương trình |1 – x| - |2x – 1| = x – 2 là
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta có |1 – x| - |2x – 1| = x – 2 (1)
Xét:
Ta có bảng xét dấu đa thức 1 – x và 2x – 1 dưới đây
Từ bảng xét dấu ta có:
TH1: x < 
1 – x – (1 – 2x) = x – 2 ⇔ 1 – x – 1 + 2x = x – 2 ⇔ x = x – 2
⇔ 0 = - 2 (vô lý)
TH2: 
TH3: x > 1, khi đó |2x – 1| = 2x – 1; |1 – x| = x – 1 nên phương trình (1) trở thành
x – 1 – (2x – 1) = x – 2 ⇔ -x + 1 = x – 2 ⇔ 2x = 3 ⇔ x = 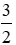
vậy phương trình có hai nghiệm x = 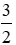
Đáp án cần chọn là: B
Bài 20: Số nghiệm của phương trình |x + 1| - |x + 2| = x + 3 là
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta có:
+) x + 1 = 0 ⇔ x = -1
+) x + 2 = 0 ⇔ x = -2
Ta có bảng:
TH2: x < -2 ta có
|x + 1| - |x + 2| = x + 3
⇔ (-x – 1) – (-x – 2) = x + 3
⇔ 1 = x + 3
⇔ x = -2 (KTM)
TH2: -2 ≤ x ≤ -1 ta có
|x + 1| - |x + 2| = x + 3
⇔ (-x – 1) – (x + 2) = x + 3
⇔ -x – 1 – x – 2 = x + 3
⇔ -2x -3 = x + 3
⇔ -3x = 6
⇔ x = -2 (TM)
TH3: x > -1 ta có
|x + 1| - |x + 2| = x + 3
⇔ (x + 1) – (x + 2) = x + 3
⇔ x + 1 – x – 2 = x + 3
⇔ -1 = x + 3
⇔x = -4 (KTM)
Vậy phương trình có nghiệm duy nhất x = -2
Đáp án cần chọn là: A
Bài 21: Cho hai phương trình 4|2x – 1| + 3 = 15 (1) và |7x + 1| - |5x + 6| = 0 (2). Kết luận nào sau đây là đúng.
A. Phương trình (1) có nhiều nghiệm hơn phương trình (2)
B. Phương trình (1) có ít nghiệm hơn phương trình (2)
C. Cả hai phương trình đều có hai nghiệm phân biệt
D. Cả hai phương trình đều vô số nghiệm
Lời giải
+) Xét phương trình 4|2x – 1| + 3 = 15 (1)
TH1: |2x – 1| = 2x – 1 khi x ≥ 
Phương trình (1) trở thành 4(2x – 1) + 3 = 15
⇔ 4(2x – 1) = 12 ⇔ 2x – 1 = 3
⇔ x = 2 (TM)
TH2: |2x – 1| = 1 – 2x khi x < 
Phương trình (1) trở thành 4(1 – 2x) + 3 = 15
⇔ 4(1 – 2x) = 12 ⇔ 1 – 2x = 3
⇔ x = -1 (TM)
Vậy phương trình (1) có hai nghiệm x = -1; x = 2
+) Xét phương trình |7x + 1| - |5x + 6| = 0
⇔ |7x + 1| = |5x + 6|
Đáp án cần chọn là: C
Bài 22: Cho hai phương trình 4|2x – 1| + 3 = 15 (1) và |7x + 1| - |5x + 6| = 0 (2). Kết luận nào sau đây là sai.
A. Phương trình (1) có hai nghiệm phân biệt
B. Phương trình (2) có hai nghiệm phân biệt
C. Hai phương trình tương đương
D. Phương trình (1) có nghiệm nguyên
Lời giải
+) Xét phương trình 4|2x – 1| + 3 = 15 (1)
TH1: |2x – 1| = 2x – 1 khi x ≥ 
Phương trình (1) trở thành 4(2x – 1) + 3 = 15
⇔ 4(2x – 1) = 12 ⇔ 2x – 1 = 3
⇔ x = 2 (TM)
TH2: |2x – 1| = 1 – 2x khi x < 
Phương trình (1) trở thành 4(1 – 2x) + 3 = 15
⇔ 4(1 – 2x) = 12 ⇔ 1 – 2x = 3
⇔ x = -1 (TM)
Vậy phương trình (1) có hai nghiệm nguyên x = -1; x = 2 nên A và D đúng
+) Xét phương trình |7x + 1| - |5x + 6| = 0
Dễ thấy các nghiệm của (1) không trùng với các nghiệm của (2) nên hai phương trình không tương đương hay C sai.
Đáp án cần chọn là: C
Bài 23: Tập nghiệm của bất phương trình |1 – x| ≥ 3 là:
A. x ≥ 4, x ≤ -2
B. -2 ≤ x ≤ 4
C. x ≤ -2, x ≤ 4
D. x ≤ 4, x ≥ -2
Lời giải
TH1: |1 – x| = 1 – x với 1 – x ≥ 0 ⇔ x ≤ 1
Bất phương trình đã cho trở thành
1 – x ≥ 3 ⇔ x ≤ -2, kết hợp điều kiện x ≤ 1 ta có x ≤ -2
TH2: |1 – x| = x – 1 với 1 – x < 0 ⇔ x > 1
Bất phương trình đã cho trở thành
x – 1 ≥ 3 ⇔ x ≥ 4, kết hợp điều kiện x > 1 ta có x ≥ 4
Vậy bất phương trình có nghiệm x ≥ 4, x ≤ -2
Đáp án cần chọn là: A
Bài 24: Nghiệm của bất phương trình |2x – 3| < 3 là:
A. x > 3
B. -3 < x < 0
C. 0 < x < 3
D. Vô nghiệm
Lời giải
TH1: 2x – 3 ≥ 0 ⇔ 2x ≥ 3 ⇔ x ≥ 
2x – 3 < 3 ⇔ 2x < 6 ⇔ x < 3
Kết hợp với x ≥ 

TH2: 2x – 3 < 0 ⇔ x < 
-2x + 3 < 3 ⇔ -2x < 0 ⇔ x > 0
Kết hợp x < 

Kết hợp nghiệm của hai trường hợp ta được:
Vậy bất phương trình có nghiêm 0 < x < 3
Đáp án cần chọn là: CBài 25: Số nguyên dương nhỏ nhất thỏa mãn bất phương trình |x – 6| + 5 ≥ x là
A. x = 0
B. x = 5
C. x = 6
D. x = 3
Lời giải
TH1: |x – 6| = x – 6 với x – 6 ≥ 0 ⇔ x ≥ 6
Bất phương trình đã cho trở thành
x – 6 + 5 ≥ x ⇔ -1 ≥ 0 (vô lý)
TH2: |x – 6| = 6 – x với x – 6 < 0 ⇔ x < 6
Bất phương trình đã cho trở thành
6 – x + 5 ≥ x ⇔ -2x ≥ -11 ⇔ x ≤ 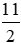
Bất phương trình có tập nghiệm S = {x Є R|x ≤ 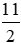
Nghiệm nguyên dương nhỏ nhất thỏa mãn là x = 5
Đáp án cần chọn là: B
Bài 26: Số nguyên dương nhỏ nhất thỏa mãn bất phương trình |-x + 2| + 5 ≥ x – 2 là
A. x = 1
B. x = 5
C. x = 6
D. Không có
Lời giải
TH1: -x + 2 ≥ 0 ⇔ x ≤ 2 thì |-x + 2| = -x + 2. Khi đó:
(-x + 2) + 5 ≥ x – 2 ⇔ -x + 7 – x + 2 ≥ 2
⇔ -2x + 9 ≥ 0 ⇔ x ≤
Kết hợp với x ≤ 2 ta được x ≤ 2
TH2: -x + 2 < 0 ⇔ x > 2 thì |-x + 2| = x – 2. Khi đó
x – 2 + 5 ≥ x – 2 ⇔ 5 > 0 (luôn đúng)
Do đó x > 2 luôn là nghiệm của bất phương trình
Vậy từ hai trường hợp ta thấy bất phương trình nghiệm đúng với mọi x Є R
Nghiệm nguyên dương nhỏ nhất thỏa mãn bất phương trình là x = 1
Đáp án cần chọn là: A
Bài 27: Nghiệm của phương trình sau đây là:
A. x = 104
B. x = 105
C. x = 103
D. x = 106
Lời giải
Điều kiện 209x ≥ 0 ⇔ x ≥ 0
Đáp án cần chọn là: A
Bài 28: Nghiệm của phương trình sau là:
Lời giải
NX: VT ≥ 0 nên VP = 2020x – 2020 ≥ 0 ⇔ x ≥ 1
Đáp án cần chọn là: A
Bài giảng Toán 8 Bài 5: Phương trình chứa dấu giá trị tuyệt đối