50 bài tập Những hằng đẳng thức đáng nhớ tiếp (có đáp án)

50 bài tập Những hằng đẳng thức đáng nhớ tiếp (có đáp án) - Toán 8

Trần Thị Hồng Ngày: 08-03-2024 Lớp 8

Tải xuống 19 1.1 K 11

Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 1 Bài 4:Những hằng đẳng thức đáng nhớ (tiếp). Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp). Mời các bạn đón xem:

Bài tập Toán 8 Chương 1 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp)

A. Bài tập Những hằng đẳng thức đáng nhớ (tiếp)

I. Bài tập trắc nghiệm

Câu 1: Biểu thức nào dưới đây viết được dưới dạng lập phương của một hiệu?

A. ${a^3} - 3a{b^2} + 3{a^2}b - {b^3}$	B. ${a^3} + 3{a^2}b - 3a{b^2} + {b^3}$
C. ${a^3} + 3{a^2}b + 3a{b^2} + {b^3}$	D. ${a^3} - 3{a^2}b + 3a{b^2} - {b^3}$

Câu 2: Biểu thức nào dưới đây viết được dưới dạng lập phương của một tổng?

A. ${x^3} - 3{x^2} + 3x - 1$	B. ${x^3} + 2{x^2} + 2x + 1$
C. $27{x^3} + 27{x^2} + 9x + 1$	D. ${x^3} - 3{x^2} + 3x + 8$

Câu 3: Có bao nhiêu giá trị x thỏa mãn: ${\left( {x + 1} \right)^3} = 1$

A. 1

B. 2

C. 3

D. 4

Câu 4: Giá trị của biểu thức ${x^3} - 6{x^2}y + 12x{y^2} - 8{y^3}$ tại x = 2021 và y = 1010 là:

A. 1

B. 4242

C. 2021

D. 1010

Câu 5: Khai triển biểu thức ${\left( {x - 1} \right)^3} - {\left( {x + 1} \right)^3}$ được:

A. $2{x^3} + 2$

B. $- 6{x^2} - 2$

C. 0

D. 1

II. Bài tập tự luận

Bài 1: Khai triển các hằng đẳng thức sau:

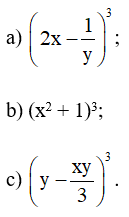
Lý thuyết Những hằng đẳng thức đáng nhớ (tiếp theo) chi tiết – Toán lớp 8 (ảnh 1)

Lời giải:

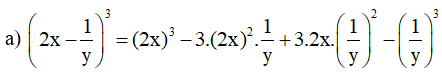
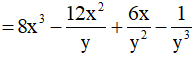
b) (x² + 1)³ = (x²)³ + 3.(x²)².1 + 3.x².1² + 1³ = x⁶ + 3x⁴ + 3x² + 1

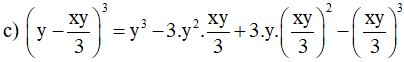
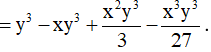
Lý thuyết Những hằng đẳng thức đáng nhớ (tiếp theo) chi tiết – Toán lớp 8 (ảnh 1)

Bài 2: Tính giá trị biểu thức.

a) P = x³ – 3x² + 3x – 1 tại x = 1001.

b) Q = 27x³y⁶ – 54x²y⁴z + 36xy²z² – 8z³ tại x = 4; y = 5; z = 150.

c) R = y³ + 3y²(1 – y) + 3y(1 – y)² + (1 – y)³ tại y = 1000.

Lời giải:

a) P = x³ – 3x² + 3x – 1

P = (x – 1)³

Thay x = 1001 vào P, ta được: P = (1001 – 1)³ = 1000³ = 1 000 000 000.

b) Q = 27x³y⁶ – 54x²y⁴z + 36xy²z² – 8z³

Q = (3xy²)³ – 3.(3xy²)².2z + 3.3xy².(2z)² – (2z)³

Q = (3xy² – 2z)³

Thay x = 4; y = 5; z = 150 vào Q, ta được: Q = (3.4.5² – 2.150)³ = 0.

c) R = y³ + 3y²(1 – y) + 3y(1 – y)² + (1 – y)³

R = (y + 1 – y)³

R = 1³

R = 1.

Vậy R = 1.

Bài 3: Tính nhanh

a) A = 102³ – 6.102² + 12.102 – 8;

b) B = 47³ + 9.47² + 27.47 + 27.

Lời giải:

a) A = 102³ – 6.102² + 12.102 – 8

A = 102³ – 3.102².2 + 3.102.2² – 2³

A = (102 – 2)³

A = 100³

A= 1 000 000

b) B = 47³ + 9.47² + 27.47 + 27

B = 47³ + 3.47².3+ 3.47.3²+ 3³

B = (47 + 3)³

B = 50³

B = 125 000

III. Bài tập vận dụng

Bài 1: Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu

a, ${x^3} - 3{x^2} + 3x - 1$	b, $- {x^3} + 6{x^2} - 12x + 8$
c, $27{y^3} - 9{y^2} + y - \frac{1}{{27}}$	d, $8{x^6} + 12{x^4}y + 6{x^2}{y^2} + {y^3}$
e, ${x^3} + 9{x^2} + 27x + 27$	f, ${\left( {x + y} \right)^3}{\left( {x - y} \right)^3}$

Bài 2: Tìm x, biết:

a, ${\left( {x + 1} \right)^2} - x\left( {x - 3} \right) = 2x + 3$

b, $\left( {x + 2} \right)\left( {x - 3} \right) - {\left( {x - 3} \right)^2} = 15$

c, ${\left( {x + 1} \right)^3} - \left( {{x^3} + 3{x^2} + 2x - 3} \right) = 0$

Bài 3: Chứng minh rằng:

a, ${a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)$

b, ${a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right)$

B. Lý thuyết Những hằng đẳng thức đáng nhớ (tiếp)

1. Lập phương của một tổng

Lập phương của một tổng bằng lập phương số thứ nhất cộng ba lần tích của bình phương số thứ nhất nhân số thứ hai cộng ba lần tích của số thứ nhất nhân bình phương số thứ hai cộng lập phương số thứ hai.

Với A, B là các biểu thức tùy ý, ta có: (A + B)³ = A³ + 3A²B + 3AB² + B³.

Ví dụ 1:

${(\frac{x}{3} + 1)}^{3} = {(\frac{x}{3})}^{3} + 3 {(\frac{x}{3})}^{2} .1 + 3. \frac{x}{3} {.1}^{2} + 1^{3} = \frac{x^{3}}{27} + \frac{x^{2}}{3} + x + 1$

(2m + n)³ = (2m)³ + 3.(2m)².n + 3.2m.n² + n³

= 8m³ + 12m²n + 6mn² + n³.

2. Lập phương của một hiệu

Lập phương của một hiệu bằng lập phương số thứ nhất trừ ba lần tích của bình phương số thứ nhất nhân số thứ hai cộng ba lần tích của số thứ nhất nhân bình phương số thứ hai trừ lập phương số thứ hai.

Với A, B là các biểu thức tùy ý, ta có: (A – B)³ = A³ – 3A²B + 3 AB² – B³

Ví dụ 2:

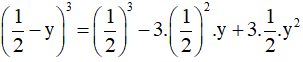
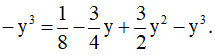
(x² – y)³ = (x²)³ – 3.(x²)².y + 3.x².y² – y³ = x⁶ – 3x⁴y + 3x²y² – y³.

Tài liệu có 19 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm