Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9 Bài 5: Công thức nghiệm rút gọn chọn lọc, có đáp án. Tài liệu có 11 trang gồm 30 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Công thức nghiệm rút gọn có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.

Giới thiệu về tài liệu:

- Số trang: 11 trang

- Số câu hỏi trắc nghiệm: 30 câu

- Lời giải & đáp án: có

Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Công thức nghiệm rút gọn có đáp án – Toán lớp 9:

Công thức nghiệm rút gọn

Câu 1: Cho phương trình ax² + bx + c = 0 (a ≠ 0) có biệt thức b = 2b’; ∆' = b² - ac Phương trình đã cho có hai nghiệm phân biệt khi?

A. ∆'  > 0   

B. ∆'  = 0    

C. ∆'  ≥ 0   

D. ∆'  ≤ 0

Lời giải:

Xét phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) với b = 2b’ và biệt thức ∆' = b² - ac

Trường hợp 1: Nếu ∆ < 0 thì phương trình vô nghiệm

Trường hợp 2: Nếu ∆ = 0 thì phương trình có nghiệm kép 

Trường hợp 3: Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt 

Đáp án cần chọn là: A

Câu 2: Cho phương trình ax² + bx + c = 0 (a ≠ 0) có biệt thức b = 2b’; ∆' = b² - ac Phương trình đã cho vô nghiệm khi?

A. ∆'  > 0   

B. ∆'  = 0    

C. ∆'  ≥ 0   

D. ∆'  ≤ 0

Lời giải:

Xét phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) với b = 2b’ và biệt thức ∆' = b² - ac

Trường hợp 1: Nếu ∆ < 0 thì phương trình vô nghiệm

Trường hợp 2: Nếu ∆ = 0 thì phương trình có nghiệm kép 

Trường hợp 3: Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt 

Đáp án cần chọn là: D

Câu 3: Cho phương trình ax² + bx + c = 0 (a ≠ 0) có biệt thức b = 2b’; ∆' = b² - ac Nếu ∆' = 0 thì?

Lời giải:

Xét phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có b = 2b’và biệt thức ∆' = b² - ac

Nếu ∆' = 0 thì phương trình có nghiệm kép 

Đáp án cần chọn là: C

Câu 4: Tính ∆' và tìm số nghiệm của phương trình 7x² − 12x + 4 = 0

A. ∆' = 6 và phương trình có hai nghiệm phân biệt

B. ∆' = 8 và phương trình có hai nghiệm phân biệt

C. ∆' = 8 và phương trình có nghiệm kép

D. ∆' = 0 và phương trình có hai nghiệm phân biệt

Lời giải:

Phương trình 7x² − 12x + 4 = 0 có a = 7; b’ = −6; c = 4 suy ra

∆' = (−6)² – 4.7 = 8 > 0

Nên phương trình có hai nghiệm phân biệt

Đáp án cần chọn là: B

Câu 5: Tính ∆' và tìm số nghiệm của phương trình 16x² − 24x + 9 = 0

A. ∆' = 432 và phương trình có hai nghiệm phân biệt

B. ∆' = − 432 và phương trình vô nghiệm

C. ∆' = 0 và phương trình có nghiệm kép

D. ∆' = 0 và phương trình có hai nghiệm phân biệt

Lời giải:

Phương trình 16x² − 24x + 9 = 0 có a = 16; b’ = −12; c = 9 suy ra

∆' = (−12)² – 9.16 = 0

Nên phương trình có nghiệm kép

Đáp án cần chọn là: C

Câu 6: Tìm m để phương trình 2mx² – (2m + 1)x − 3 = 0 có nghiệm là x = 2

Lời giải:

Thay x = 2 vào phương trình 2mx² – (2m + 1)x − 3 = 0, ta được:

Đáp án cần chọn là: C

Câu 7: Tìm m để phương trình (3m + 1)x² – (5 – m)x − 9 = 0 có nghiệm là x = −3

Lời giải:

Thay x = −3 vào phương trình (3m + 1)x² – (5 – m)x − 9 = 0 ta được

Đáp án cần chọn là: D

Câu 8: Tính ∆' và tìm nghiệm của phương trình 

A. ∆' = 5 và phương trình có hai nghiệm 

B. ∆' = 5 và phương trình có hai nghiệm  

C. ∆' = √5 và phương trình có hai nghiệm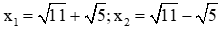  

D. ∆' = 5 và phương trình có hai nghiệm  

Lời giải:

Phương trình 2x² + 2 x + 3 = 0 có a = 2; b’ = ; c = 3 suy ra

∆' = b² - ac = 11 – 2.3 = 5 > 0 nên phương trình có hai nghiệm phân biệt

  

Đáp án cần chọn là: D

Câu 9: Tính ∆' và tìm nghiệm của phương trình 3x² − 2x = x² + 3

A. ∆' = 7 và phương trình có hai nghiệm  

B. ∆' = 7 và phương trình có hai nghiệm 

C. ∆' = √7 và phương trình có hai nghiệm 

D. ∆' = 7 và phương trình có hai nghiệm 

Lời giải:

Phương trình 3x² − 2x = x² + 3 ⇔ 2x² – 2x – 3 = 0 có a = 2; b’ = −1; c = −3

Suy ra ∆' = b² - ac = (−1)² – 2.(−3) = 7 > 0 nên phương trình có hai nghiệm phân biệt là:

  

Đáp án cần chọn là: B

Câu 10: Cho phương trình mx² – 2(m – 1)x + m – 3 = 0. Với giá trị nào dưới đây của m thì phương trình không có hai nghiệm phân biệt

Lời giải:

Phương trình mx² – 2(m – 1)x + m – 3 = 0 có a = m; b’ = − (m – 1); c = m – 3

Suy ra ∆' = [− (m – 1)]² – m(m − 3) = m + 1

Để phương trình có hai nghiệm phân biệt thì 

Nên với đáp án A: 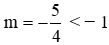  thì phương trình không có hai nghiệm phân biệt

Đáp án cần chọn là: A

Câu 11: Cho phương trình (m + 1)x² – 2(m + 1)x + 1 = 0. Tìm các giá trị của m để phương trình có hai nghiệm phân biệt

A. m > 0     

B. m < −1   

C. −1 < m < 0       

D. Cả A và B đúng

Lời giải:

Phương trình (m + 1)x² – 2(m + 1)x + 1 = 0 có a = m + 1; b’ = − (m + 1); c = 1

Suy ra ∆' = [− (m + 1)]² – (m + 1) = m² + m

Để phương trình (m + 1)x² – 2(m + 1)x + 1 = 0 có hai nghiệm phân biệt thì:

Vậy m > 0 hoặc m < −1 thì phương trình có hai nghiệm phân biệt

Đáp án cần chọn là: D

Câu 12: Cho phương trình (m – 3)x² – 2mx + m − 6 = 0. Tìm các giá trị của m để phương trình vô nghiệm

A. m < −2   

B. m < 2     

C. m < 3     

D. m < −3

Lời giải:

Phương trình (m – 3)x² – 2mx + m − 6 = 0 có a = m – 3; b’ = −m; c = m – 6

Suy ra ∆' = (−m)² – (m − 3)(m – 6) = 9m – 18

Đáp án cần chọn là: B

Câu 13: Cho phương trình mx² – 4(m – 1) x + 2 = 0. Tìm các giá trị của m để phương trình vô nghiệm.

Lời giải:

Phương trình mx² – 4(m – 1) x + 2 = 0 có a = m; b’ = −2(m – 1); c = 2

Suy ra ∆' = [−2(m – 1)]² – m.2 = 4m² – 10m + 4

TH1: m = 0 ta có phương trình 4x + 2 = 0 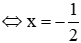 nên loại m = 0

TH2: m ≠ 0. Để phương trình vô nghiệm thì

Đáp án cần chọn là: C

Câu 14: Cho phương trình (m – 2)x² – 2(m + 1)x + m = 0. Tìm các giá trị của m để phương trình có một nghiệm.

Lời giải:

Phương trình (m – 2)x² – 2(m + 1)x + m = 0 có a = m – 2; b’ = − (m + 1); c = m

Suy ra ∆' = [−(m + 1)]² – (m – 2).m = 4m + 1

Với m = 2 thì phương trình có một nghiệm 

Đáp án cần chọn là: B

Câu 15: Tìm m để phương trình có nghiệm kép và tìm nghiệm kép đó

Lời giải:

Để phương trình mx² – 2(m – 1)x + 2 = 0 có nghiệm kép thì

Đáp án cần chọn là: D

Câu 16: Tìm các giá trị của m để phương trình mx² – 2(m – 1)x + m + 2 = 0 có nghiệm.

Lời giải:

Phương trình mx² – 2(m – 1)x + m + 2 = 0 có a = m; b’ = − (m – 1); c = m + 2

Suy ra ∆' = (m – 1)² – m(m + 2) = −4m + 1

TH1: m = 0, ta có phương trình 2x + 2 = 0 ⇔ x = −1

TH2: m ≠ 0. Phương trình có nghiệm khi 

Kết hợp cả hai trường hợp ta có với 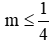 thì phương trình có nghiệm

Đáp án cần chọn là: A

Câu 17: Phương trình (m – 3)x² – 2(3m + 1)x + 9m – 1 = 0 có nghiệm khi?

Lời giải:

Phương trình (m – 3)x² – 2(3m + 1)x + 9m – 1 = 0 có a = m – 3; b’ = − (3m + 1) và c = 9m – 1

TH1: Nếu m – 3 = 0 ⇒ m = 3 thì phương trình (m – 3)x² – 2(3m + 1)x + 9m – 1 = 0 trở thành −2(3.3 + 1) x + 9.3 – 1 = 0 ⇒ −20x + 26 = 0 ⇒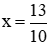   

Vậy m = 3 thì phương trình có nghiệm duy nhất nên ta nhận m = 3

TH2: m ≠ 3 thì phương trình là phương trình bậc hai. Phương trình có nghiệm khi

Đáp án cần chọn là: A

Câu 18: Trong trường hợp phương trình −x² + 2mx − m² – m = 0 có hai nghiệm phân biệt. Hai nghiệm của phương trình là?

Lời giải:

Phương trình −x² + 2mx − m² – m = 0 có a = −1; b’ = m; c = −m² – m

Suy ra ∆' = m² – (−1).( −m² – m) = −m

Phương trình có hai nghiệm phân biệt khi –m > 0 ⇔ m < 0

Đáp án cần chọn là: A

Câu 19: Trong trường hợp phương trình x² – 2(m – 2)x + 2m − 5 = 0 có hai nghiệm phân biệt. Hai nghiệm của phương trình là?

Lời giải:

Phương trình x² – 2(m – 2)x + 2m − 5 = 0 có a = 1; b’ = − (m – 2); c = 2m – 5

Suy ra ∆' = [− (m – 2)]² – 1.(2m − 5) = m² – 6m + 9 = (m – 3)²

Để phương trình có hai nghiệm phân biệt thì ∆' > 0 ⇔ (m – 3)² > 0 ⇔ m ≠ 3

Khi đó, phương trình có hai nghiệm phân biệt là:

  

Đáp án cần chọn là: B

Câu 20: Cho phương trình x² + (a + b + c)x + (ab + bc + ca) = 0 với a, b, c là ba cạnh của một tam giác. Khẳng định nào sau đây là đúng?

A. Phương trình luôn có hai nghiệm phân biệt

B. Phương trình luôn có nghiệm kép

C. Chưa đủ điều kiện để kết luận

D. Phương trình luôn vô nghiệm

Lời giải:

Phương trình x² + (a + b + c)x + (ab + bc + ca) = 0

Có ∆ = (a + b + c)² − 4(ab + bc + ca) = a² + b² + c² – 2ab – 2bc – 2ac

= (a – b)² – c² + (b – c)² – a² + (a – c)² – b²

= (a – b – c)(a + c – b) + (b – c – a)(a + b – c) + (a – c – b)(a – c + b)

Mà a, b, c là ba cạnh của một tam giác nên  

Nên ∆ < 0 với mọi a, b, c

Hay phương trình luôn vô nghiệm với mọi a, b, c

Đáp án cần chọn là: D

Câu 21: Cho phương trình b²x² – (b² + c² – a²)x + c² = 0 với a, b, c là ba cạnh của một tam giác. Khẳng định nào sau đây là đúng?

A. Phương trình luôn có hai nghiệm phân biệt

B. Phương trình luôn có nghiệm kép

C. Chưa đủ điều kiện để kết luận

D. Phương trình luôn vô nghiệm

Lời giải:

Phương trình b²x² – (b² + c² – a²)x + c² = 0

Có ∆ = (b² + c² – a²) – b²c² = (b² + c² – a² + 2bc)(b² + c² – a² – 2bc)

= [(b + c)² – a²] [(b – c)² – a²]

= (b + c + a)(b + c – a)(b – c – a)(b – c + a)

Mà a, b, c là ba cạnh của tam giác nên 

Nên ∆ < 0 với mọi a, b, c

Hay phương trình luôn vô nghiệm với mọi a, b, c

Đáp án cần chọn là: D

Bài giảng Toán 9 Bài 5: Công thức nghiệm thu gọn