Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 1 Bài 2: Hình thang. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 2: Hình thang. Mời các bạn đón xem:

Bài tập Toán 8 Chương 1 Bài 2: Hình thang

A. Bài tập Hình thang

I. Bài tập trắc nghiệm

Bài 1: Chọn câu đúng trong các câu sau:

A. Hình thang có ba góc tù, một góc nhọn.

B. Hình thang có ba góc vuông, một góc nhọn.

C. Hình thang có ba góc nhọn, một góc tù.

D. Hình thanh có nhiều nhất hai góc nhọn và nhiều nhất hai góc tù.

Lời giải:

Ta có tổng các góc của hình thang bằng 360⁰.

+ Hình thang có ba góc tù, một góc nhọn.

Ví dụ: Hình thang có 3 góc tù là 100⁰,120⁰,135⁰ và 1 góc nhọn là 60⁰.

⇒ Tổng 4 góc của hình thang bằng 100⁰ + 120⁰ + 135⁰ + 60⁰ = 415⁰ > 360⁰

⇒ Không tồn tại hình thang có ba góc tù, một góc nhọn. ⇒ Đáp án A sai

+ Hình thang có ba góc vuông, một góc nhọn.

Ví dụ: Hình thang có 3 góc bằng 90⁰ và một góc nhọn bằng 65⁰

⇒ Tổng 4 góc của hình thang bằng 90⁰ + 90⁰ + 90⁰ + 65⁰ = 335⁰ < 360⁰

⇒ Không tồn tại hình thang ba góc vuông, một góc nhọn. ⇒ Đáp án B sai.

+ Hình thang có ba góc nhọn, một góc tù.

Ví dụ: Hình thang có ba góc nhọn là 45⁰,75⁰,80⁰, một góc tù là 160⁰

⇒ Tổng 4 góc của hình thang bằng 45⁰ + 75⁰ + 80⁰ + 160⁰ = 360⁰

⇒ Tồn tại Hình thang có ba góc nhọn, một góc tù. ⇒ Đáp án C đúng

⇒ Hình thang có nhiều nhất là 3 góc nhọn. ⇒ Đáp án D sai.

Chọn đáp án C.

Bài 2: Một hình thang có một cặp góc đối là 125⁰ và 75⁰, cặp góc đối còn lại của hình thang đó là ?

A. 105⁰,55⁰   

B. 105⁰,45⁰

C. 115⁰,55⁰   

D. 115⁰,65⁰

Lời giải:

Tổng bốn góc của hình thang bằng 360⁰.

Theo giả thiết ta có một cặp góc đối là 125⁰ và 75⁰

⇒ Tổng số đo góc của cặp góc đối còn lại là 160⁰.

Xét đáp án ta có cặp 105⁰,55⁰ thỏa mãn.

Chọn đáp án A.

Bài 3: Hình thang ABCD có $\hat{C}+\hat{D}$ˆ = 150⁰. Khi đó $\hat{A}+\hat{B}$ˆ = ?

A. 220⁰   

B. 210⁰

C. 200⁰   

D. 190⁰

Lời giải:

Tổng bốn góc của hình thang bằng 360⁰.

Khi đó ta có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}$ˆ = 360⁰ ⇒ $\hat{A}+\hat{B}$ˆ = 360⁰ - ( $\hat{C}+\hat{D}$ˆ )

⇒ $\hat{A}+\hat{B}$ˆ = 360⁰ - 150⁰ = 210⁰.

Chọn đáp án B.

Bài 4: Cho hình thang ABCD trong đó có $\hat{A}$ = 120⁰, $\hat{B}$ˆ = 60⁰, $\hat{D}$ = 135⁰ thì số đo của góc $\hat{C}$ˆ = ?

A. 55⁰   

B. 45⁰

C. 50⁰   

D. 60⁰

Lời giải:

Tổng bốn góc của hình thang bằng 360⁰.

Khi đó ta có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}$ˆ = 360⁰ ⇒ $\hat{C}$ = 360⁰ - ( $\hat{A}+\hat{B}+\hat{D}$ˆ )

⇒ $\hat{C}$ = 360⁰ - ( 120⁰ + 60⁰ + 135⁰ ) = 45⁰.

Chọn đáp án B.

Bài 5: Cho hình thang ABCD có AB // CD. Biết $\hat{A}$ˆ = 100^o, tính $\hat{D}$ˆ

A. 80^o    

B. 100^o

C. 120^o    

D. 50^o

Lời giải:

Chọn đáp án A

Bài 6: Cho hình thang ABCD có AB // CD và $\hat{A}$ˆ = 120^o, $\hat{B}$ˆ = 120^o. Tính $\hat{C}, \hat{D}$ˆ

Lời giải:

Chọn đáp án A

Bài 7: Cho hình thang vuông ABCD vuông tại A và D. Biết AD = 3 cm và CD = 4cm. Tính AC?

A. 3cm    

B. 4cm

C. 3,5cm    

D. 5cm

Lời giải:

Do tứ giác ABCD là hình thang vuông nên $\hat{D}$ˆ = 90^o

Suy ra, tam giác ADC là tam giác vuông tại D.

Áp dụng đinh lí Py ta go vào tam giác vuông ACD ta có:

AC² = AD² + DC² = 3² + 4² = 25

Suy ra: AC = 5cm

Chọn đáp án D

Bài 8: Cho tứ giác lồi ABCD có AB // CD và AD = 6cm; DC = 8cm và AC = 10cm. Tìm khẳng định sai ?

A. Tam giác ADC vuông tại D.

B. Tứ giác ABCD là hình thang

C. Tứ giác ABCD là hình thang vuông có $\hat{D}$ˆ = 90^o

D. Tứ giác ABCD là hình thang vuông có $\hat{B}$ˆ = 90^o

Lời giải:

Tứ giác ABCD có AB // CD nên tứ giác ABCD là hình thang có 2 đáy là AB và CD.

Xét tam giác ACD có: AD² + CD² = AC² (6² + 8² = 10² = 100)

Suy ra: tam giác ADC là tam giác vuông tại D.

Do đó: $\hat{D}$ˆ = 90^o

Suy ra: Tứ giác ABCD là hình thang vuông có $\hat{D}$ˆ = 90^o

Vậy khẳng định D sai

Chọn đáp án D

Bài 9: Cho hình thang ABCD có AB // CD và $\hat{A}=2\hat{D}$ˆ. Tính góc $\hat{A}$?

A. 60^o    

B. 120^o

C. 90^o    

D. 80^o

Lời giải:

Chọn đáp án B

Bài 10: Cho hình thang ABCD có AB // CD và $\hat{C}-\hat{D}$ = 30^o . Tính góc C?

A. 105^o    

B. 90^o

C. 75^o    

D. 60^o

Lời giải:

Chọn đáp án A

Bài 11: Cho hình thang ABCD có 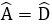 = 90⁰, DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.

A. 110⁰           

B. 150⁰           

C. 120⁰                       

D. 135⁰

Lời giải:

Từ B kẻ BE vuông góc với CD tại E.

Tứ giác ABED là hình thang có hai cạnh bên AD // BE nên AD = BE, AB = DE.

Mặt khác, DC = BC = 2AB nên DC = 2ED, do đó E là trung điểm của DC.

Xét ΔBDE và ΔBCE có 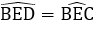 = 900; DE = EC; BE cạnh chung nên ΔBED = ΔBEC (c – g – c)

Suy ra BD = BC mà BC = DC (gt) ⇒ BD = BC = CD nên ΔBCD đều.

Xét ΔBCD đều có BE là đường cao cũng là đường phân giác nên

Đáp án cần chọn là: C

Bài 12: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE.

Tứ giác BDEC là hình gì?

A. Hình thang                        

B. Hình thang vuông

C. Hình thang cân                              

D. Cả A, B, C đều sai

Lời giải:

Tam giác ADE có AD = AE (gt) nen tam giác ADE cân tại A.

Suy ra 

Tam giác ABC cân tại A (gt) nên 

Từ (1) và (2) suy ra 

Mà 2 góc  là hai góc ở vị trí đồng vị nên suy ra DE // BC

Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang

Lại có  (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

Đáp án cần chọn là: C

Bài 13: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC.

Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?

A. Hình thang                        

B. Hình thang vuông

C. Hình thang cân                              

D. Cả A, B, C đều sai

Lời giải:

Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.

Lại có 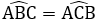 (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

Đáp án cần chọn là: C

Bài 14: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.

1. Chọn khẳng định đúng nhất?

A. Tứ giác BDIC là hình thang                     

B. Tứ giác BIEC là hình thang

C. Tứ giác BDEC là hình thang                    

D. Cả A, B, C đều đúng

Lời giải

Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.

Tương tự:

Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.

Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.

Đáp án cần chọn là: D

2. Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.

Chọn khẳng định đúng.

A. DE > BD + CE                              

B. DE = BD + CE

C. DE < BD + CE                              

D. BC = BD + CE

Lời giải

Suy ra tam giác EIC cân đỉnh E

Do đó EI = EC (2)

Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE

⇒ DE = BD + CE

Đáp án cần chọn là: B

Bài 15: Cho hình thang cân MNPQ (MN // PQ) có góc 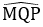 = 45⁰ và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:

A. 728 cm²     

B. 346 cm²     

C. 364 cm²     

D. 362 cm²

Lời giải:

Kẻ MH ⊥ QP; NK ⊥ QP tại H, K ⇒ MH // NK

Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK

⇒ MN = HK; MH = NK

(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)

Lại có

MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)

Mà HK = MN = 12 cm nên QH = KP = 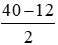 = 14 cm

Mà 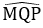 = 450 ⇒ ΔMHQ vuông cân tại H ⇒ MH = QH = 14 cm

Diện tích hình thang cân MNPQ là

SMNPQ = 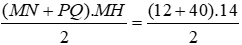 = 364 cm2

Đáp án cần chọn là: C

II. Bài tập tự luận có lời giải

Bài 1: Một hình thang có hiệu của đáy lớn và đáy bé bằng 21cm, đáy bé bằng  đáy lớn, chiều cao bằng 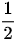 đáy bé. Hãy tìm diện tích của hình thang nói trên.

Lời giải: Đáp số: $539c{m}^2$

Bài 2: Một hình thang vuông có đáy bé bằng 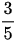 đáy lớn và chiều cao bằng 23cm, người ta mở rộng hình thang để được một hình chữ nhật thì diện tích của nó tăng thêm lên . Hãy tính diện tích hình thang lúc đầu.

Lời giải:

 Gợi ý: Phần mở rộng là một tam giác vuông, có cạnh góc vuông bằng chiều cao của hình thang. Số đo cạnh góc vuông còn lại bằng

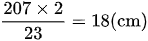
18cm chính là hiệu số đo hai đáy của hình thang. Coi đáy bé hình thang gồm ba phần bằng nhau thì đáy lớn gồm 5 phần. Hiệu số phần bằng nhau là:

5 – 3 = 2 (phần)

Đáy lớn của hình thang bằng:

(18 : 2) x 5 = 45 (cm)

Đáy bé của hình thang bằng

45 – 18 = 27 (cm)

Diện tích hình thang lúc đầu là:

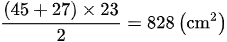
Đáp số: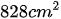 

Bài 3: Một miếng đất hình thang có diện tích 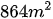, đáy lớn hơn đáy bé 12m. Người ta mở rộng miếng đất bằng cách tăng đáy lớn thêm 5m thì được miếng đất hình thang có diện tích bằng 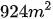. Tìm độ dài đáy lớn, đáy bé của miếng đất hình thang lúc chưa mở rộng.

Lời giải:

Sau khi mở rộng, diện tích đất tăng thêm là:

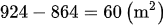
Phần tăng thêm có dạng hình tam giác, có đáy bằng 5m, chiều cao bằng chiều cao của miếng đất hình thang, chiều cao đó bằng:

60 x 2 : 5 = 24 (m)

Tổng hai đáy của hình thang lúc chưa mở rộng bằng:

864 x 2 : 24 = 72 (m)

Hai lần đáy bé bằng:

72 – 12 = 60 (m)

Đáy bé bằng:

60 : 2 = 30 (m)

Đáy lớn lúc chưa mở rộng bằng:

30 + 12 = 42 (m)

Đáp số: 30m; 42m

Bài 4: Cho hình thang ABCD có diện tích 1000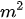. Trên cạnh bên AD lấy hai điểm M, N sao cho AM bằng ND và bằng 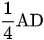. Từ M và N kẻ các đường song song với hai đáy AB và CD, chúng lần lượt cắt cạnh BC tại P và Q. Tính diện tích hình tứ giác MNQP.

Lời giải:

Kẻ hai đường chéo AC và BD, khi đó 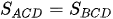 và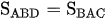 

Vì MP song song với NQ và DC nên các tứ giác ABPM;; MPQN; NQCD đều là các hình thang, nên:

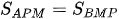 VÀ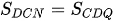 

Ta có: 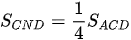 (vì đáy ND bằng  và chúng có chung chiều cao hạ từ đỉnh C xuống AD).

Ta có: 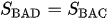 và 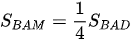. Suy ra

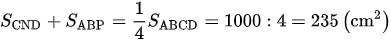
Từ đó:

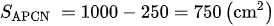
Nối NP, ta có:

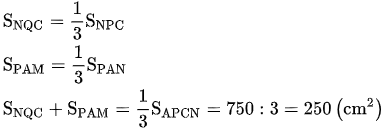
Từ đó suy ra:

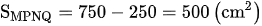
Đáp số: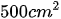 

Bài 5: Cho hình thang ABCD có diện tích 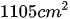, đáy lớn 47cm, đáy bé 38cm. Đoạn đường BD chia hình thang thành hai tam giác ABD và BCD. Hãy tính diện tích mỗi tam giác.

Lời giải:

Đáp số: $S_{BCD}=611c{m}^2; S_{ADB}=494c{m}^2$

Bài 6: Một hình thang có diện tích 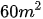, hiệu của hai đáy bằng 4m. Hãy tính độ dài mỗi đáy, biết rằng nếu đáy lớn được tăng thêm 2m thì diện tích hình thang sẽ tăng thêm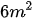 

Lời giải:

Ta có:

Chiều cao BH của tam giác BCE (phần mở rộng là):

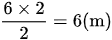
Đó cũng là chiều cao của hình thang.

Tổng của hai đáy là:

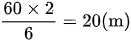
Đáy bé là:

(20 – 4) : 2 = 8 (m)

Đáy lớn là:

8 + 4 = 12 (m)

Đáp số: Đáy bé: 8m; Đáy lớn: 12m

Bài 7: Một thửa ruộng hình thang có diện tích là 1155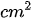 và có đáy bé kém đáy lớn 33m. Người ta kéo dài đáy bé thêm 20m và kéo dài đáy lớn thêm 5m về cùng một phía để được hình thang mới. Diện tích hình thang mới này bằng diện tích của một hình chữ nhật có chiều rộng là 30m và chiều dài 51m. Hãy tính đáy bé, đáy lớn của thửa ruộng ban đầu.

Lời giải:

Hình thang AEGD có diện tích bằng diện tích của một hình chữ nhật có chiều rộng 30m và chiều dài 51m

Do đó diện tích hình thang AEGD là:

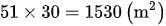
Diện tích phần tăng thêm BEGC là:

1530 – 1155 = 375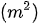 

Chiều cao BH của hình thang BEGC là:

375 x 2 : (20 + 5) = 30 (m)

Chiều cao BH cũng là chiều cao của hình thang ABCD. Do đó tổng hai đáy AB và CD là:

1155 x 2 : 30 = 77 (m)

Đáy bé là:

(77 – 33) : 2 = 22 (m)

Đáy lớn là:

77 – 22 = 55 (m)

Đáp số: Đáy bé: 22m; đáy lớn: 55m.

Bài 8: Cho hình thang ABCD có hai đáy là AB và CD. Biết AB = 15cm, CD = 20cm, chiều cao hình thang là 14cm. Hai đường chéo AC và BD cắt nhau ở E.

a) Tính diện tích hình thang ABCD

b) Chứng minh hai tam giác AED và BEC có diện tích bằng nhau

c) Tính diện tích tam giác CED.

Lời giải:

a) Gọi S là diện tích hình ABCD thì:

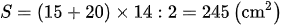
b) Ta có: 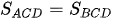 (do đây là hai tam giác chung đáy DC và chung chiều cao)

Hai tam giác này lại có chung nhau phần diện tích tam giác DEC nên hai phần còn lại là tam giác AED và tam giác BEC phải có diện tích bằng nhau.

c) Ta có tam giác ABC và tam giác ADC là hai tam giác có cùng đường cao chính là đường cao của hình thang ABCD nên tỉ số diện tích của chúng là tỉ số của cạnh .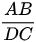

Hai tam giác ABC và ADc này lại chung đáy AC nên 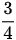 cũng là tỉ lệ chiều cao của chúng và đồng thời là tỉ lệ diện tích và bằng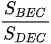 

Tổng diện tích cả hai tam giác BEC và DEC (chính là diện tích tam giác BCD) là:

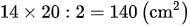
Vậy diện tích tam giác DEC là:

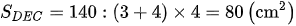
Đáp số: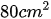 

Bài 9: Cho hình thang ABCD, MA = MC; MN song song BD (hình vẽ). Giải thích tại sao BN chia hình thang thành hai phần có diện tích bằng nhau ?

Lời giải:

Vì MN song song BD nên 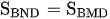 và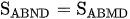 

Vì  nên ;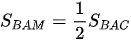 

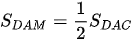
Như v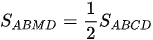ậy  hay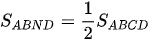 

Suy ra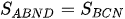 

Bài 10: Hình thang ABCD (AB // CD) có $\hat{A}-\hat{D}={20}^{\circ };\hat{B}=2\hat{C}$. Tính các góc của hình thang.

Hướng dẫn:

Hình thang ABCD có AB // CD nên:

$\hat{A}+\hat{D}={180}^{\circ }$ và $\hat{B}+\hat{C}={180}^{\circ }$ (trong cùng phía)

Ta có: 

+) $\hat{A}+\hat{D}={180}^{\circ };\hat{A}-\hat{D}={20}^{\circ }\Rightarrow \hat{A}={100}^{\circ };D=\widehat{{80}^{\circ }}$

+) $\hat{B}+\hat{C}={180}^{\circ };\hat{B}=2\hat{C}\Rightarrow \hat{B}={120}^{\circ };\hat{C}={60}^{\circ }$

Bài 11: Hình thang vuông ABCD có $\hat{A}=\hat{D}={90}^{\circ }$; AB = AD = 3cm; DC = 6cm. Tính các góc B và C của hình thang.

Hướng dẫn:

Kẻ BE $\perp$ CD thì AD // BE, do cùng vuông góc với CD nên hình thang ABED có hai cạnh bên song song.

$\Rightarrow$ BE = AD = 3cm; DE = AB = 3cm. Do đó EC = DC - DE = 6cm - 3cm = 3cm

$\Rightarrow \mathrm{\Delta }BCE$ vuông cân tại E nên $\hat{C}={45}^{\circ }$

Do $\hat{B}$ và $\hat{C}$ là hai góc trong cùng phía của AB // DC nên chúng bù nhau hay $\hat{B}+\hat{C}={180}^{\circ }\Rightarrow \hat{B}={180}^{\circ }-{45}^{\circ }={135}^{\circ }$

Bài 12: Cho hình thang cân ABCD có AB // CD, AB < CD. Kẻ các đường cao AH, BK của hình thang. Chứng minh rằng DH = CK.

Hướng dẫn:

Áp dụng định nghĩa, tính chất và giải thiết vào hình thang cân ABCD ta được:

• $\hat{D}=\hat{C}$
• AD = BC
• $\hat{H}=\hat{K}={90}^{\circ }$

$\Rightarrow \mathrm{\Delta }$ADH = $\mathrm{\Delta }$BCK (trường hợp cạnh huyền - góc nhọn)

$\Rightarrow$ DH = CK

Bài 13: Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, các cạnh đáy AB = 6cm và CD = 14cm.

Hướng dẫn:

Kẻ $AH\perp DC;BK\perp DC$ thì AH // BK nên hình thang ABKH có hai cạnh bên song song.

$\Rightarrow$ AH = BK, HK = AB = 6cm

Áp dụng định lí Py-ta-go vào $\mathrm{\Delta }$ADH vuông tại H ta được:

$A{D}^2=D{H}^2+H{A}^2$ hay $5^2=4^2+H{A}^2$

$\iff H{A}^2=9\iff HA=3$(cm)

Vậy chiều cao của hình thang cân là 3cm.

Bài 14: Tính x, y trên hình.

Hướng dẫn:

Do IP, GK, MH cùng vuông góc với AH nên IP // GK // MH

Lại có AI = IG = GM

$\Rightarrow$ AP = PK = KH, do đó IP là đường trung bình của tam giác AGK; GK là đường trung bình của hình thang IPHM.

Áp dụng định lí đường trung bình vào tam giác AGK và hình thang IPHM ta được: GK = 2IP hay 6cm = 2x $\iff$ x = 3cm

GK = $\frac{IP+MH}{2}$ hay $6=\frac{3+y}{2}\iff y=9$ (cm)

2. Vẽ thêm đường trung bình để chứng minh quan hệ về độ dài

Ta vẽ thêm đường trung bình. Sau đó áp dụng định lí đường trung bình của tam giác, của hình thang.

Bài 15: Cho $\mathrm{\Delta }$ABC có AM là đường trung tuyến. Gọi I là trung điểm của AM và D là giao điểm của CI và AB. Chứng minh rằng: DA = $\frac{1}{2}$DB; DI = $\frac{1}{4}$DC.

Hướng dẫn:

Do M là trung điểm của BC theo giả thiết nên vẽ thêm E là trung điểm của BD thì BE = ED (1)

Ta được EM là đường trung bình của $\mathrm{\Delta }$BCD

Áp dụng định lí đường trung bình vào $\mathrm{\Delta }$BCD, ta được:

ME // DC (2) và DC = 2ME (3)

Từ (2) $\Rightarrow$ ME // DI mà AI = IM theo giả thiết

Áp dụng định lí đường trung bình vào $\mathrm{\Delta }$AME ta được AD = DE (4)

Từ (1) và (4) suy ra AD = DE = EB (5) hay AD = $\frac{1}{2}$DB

Từ (4) và (5) ta có DI là đường trung bình của $\mathrm{\Delta }$AEM.

Áp dụng định lí đường trung bình vào $\mathrm{\Delta }$AEM ta có ME = 2DI (6)

Thay (6) vào (3) ta được: DC = 2.2DI = 4DI hay DI = $\frac{1}{2}$DC

3. Vẽ thêm đường trung bình để chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng

Ta vẽ thêm đường trung bình

Áp dụng định lí đường trung bình của tam giác, của hình thang

Sử dụng tiên đề Ơ-clít về đường thẳng song song: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó hoặc sử dụng tính chất: Nếu một góc là góc bẹt thì hai cạnh của góc ấy là hai tia đối nhau hay hai cạnh của góc này nằm trên một đường thẳng.

III. Bài tập vận dụng

Bài 1 Tìm x và y trên h.21, biết rằng ABCD là hình thang có đáy AB và CD.

Bài 2 Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem h.19). Trên h.20, có những tứ giác là hình thang, có những tứ giác không phải là hình thang. Bằng cách trên, hãy kiểm tra xem trong các tứ giác ở h.19, tứ giác nào là hình thang?

Bài 3 Hình thang ABCD (AB // CD) có

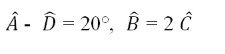
Tính các góc của hình thang.

Bài 4 Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.

Bài 5 Đố

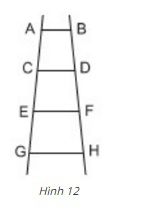
Hình 12 vẽ một chiếc thang. Trên hình vẽ có bao nhiêu hình thang?

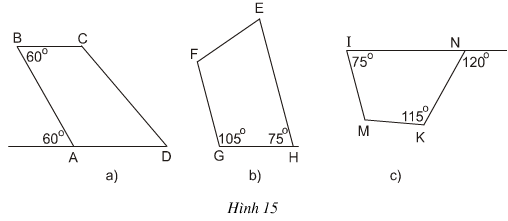
Bài 6 Cho hình 15.

a) Tìm các tứ giác là hình thang.

b) Có nhận xét gì về hai góc kề một cạnh bên của hình thang ?

Bài 7 Hình thang ABCD có đáy AB, CD.

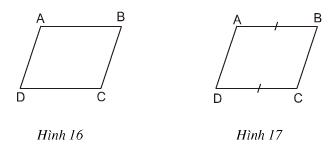
Cho biết AD // BC (hình 16). Chứng minh: AD = BC, AB = CD.

Cho biết AB = CD (hình 17). Chứng minh: AD // BC, AD = BC.

Bài 8 Cho hình 15.

a) Tìm các tứ giác là hình thang.

b) Có nhận xét gì về hai góc kề một cạnh bên của hình thang ?

Bài 9 Hình thang ABCD có đáy AB, CD.

a) Cho biết AD // BC (h.16). Chứng minh rằng AD = BC, AB = CD.

b) Cho biết AB = CD (h.17). Chứng minh rằng AD // BC, AD = BC.

Bài 10 Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem hình 19). Trên hình 20, có những tứ giác là hình thang, có những tứ giác không là hình thang. Bằng cách nêu trên, hãy kiểm tra xem trong các tứ giác ở hình 19, tứ giác nào là hình thang?

Bài 11 Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy là AB và CD.

Bài 12 Hình thang ABCD (AB // CD) có 

Tính các góc của hình thang.

Bài 13 Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.

Bài 14 Hình 12 là hình vẽ một chiếc thang. Trên hình vẽ có bao nhiêu hình thang?

Bài 15 Một hình thang có một cặp góc đối là 135⁰ và 75⁰, cặp góc đối còn lại của hình thang đó là ?

Bài 16 Cho hình thang ABCD có hai đáy là AB và CD. Biết AB = 15cm, CD = 20cm, chiều cao hình thang là 14cm. Hai đường chéo AC và BD cắt nhau ở E.

a) Tính diện tích hình thang ABCD

b) Chứng minh hai tam giác AED và BEC có diện tích bằng nhau

c) Tính diện tích tam giác CED.

Bài 17 Cho hình thang ABCD có (AB//CD) có  và . Tính các góc của hình thang?

Bài 18 Cho hình thang ABCD (AB//CD). Tính số đo các góc chưa biết.

Bài 19 Cho tứ giác ABCD, AB=BC và AC là tia phân giác của góc A. Chứng minh ABCD là hình thang.

Bài 20 Cho tam giác ABC vuông tại A, lấy điểm M thuộc cạnh BC sao cho , N là trung điểm cạnh AB.

B. Lý thuyết Hình thang

1. Định nghĩa

Hình thang là tứ giác có hai cạnh đối song song.

   Hai cạnh song song gọi là hai đáy.

   Hai cạnh còn lại gọi là hai cạnh bên.

Gọi AH là đường vuông góc kẻ từ A đến đường thẳng CD, đoạn thẳng AH được gọi là đường cao của hình thang

Nhận xét:

   Nếu một hình thang có hai cạnh bên song song thì hai canh bên bằng nhau, hai cạnh đáy bằng nhau.

   Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.

2. Hình thang vuông

Định nghĩa: Hình thang vuông là hình thang có một góc vuông

Dấu hiệu nhận biết: Hình thang có một góc vuông là hình thang vuông

Ví dụ: Cho hình thang ABCD ( AB//CD ) có Aˆ - Dˆ = 30⁰,Bˆ = 2Cˆ. Tính các góc của hình thang

Hướng dẫn:

Trong hình thang ABCD có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰.       ( 1 )

Theo giả thiết, ta có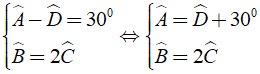       ( 2 )

Ta lại có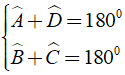       ( 3 ) (do góc Dˆ bằng góc ngoài của góc Aˆ, góc Cˆ bằng góc ngoài của góc Bˆ )

Từ ( 2 ),( 3 ) ta có

Khi đó Aˆ = Dˆ + 30^o = 75^o + 30^o = 105^o; Bˆ = 2Cˆ = 120⁰.