Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 3 Bài 7:Tứ giác nội tiếp. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 7: Tứ giác nội tiếp. Mời các bạn đón xem:
Bài tập Toán 9 Chương 3 Bài 7: Tứ giác nội tiếp
A. Bài tập Tứ giác nội tiếp
I. Bài tập trắc nghiệm
Câu 1: Cho tứ giác ABCD nội tiếp đường tròn (O) (hình 1) . Chọn khẳng định sai?
(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )
Phương án A, B, C đúng
Chọn đáp án D
Câu 2: Tứ giác ở hình nào dưới đây là tứ giác nội tiếp?
A. Hình 2
B. Hình 3
C. Hình 4
D. Hình 5
Lời giải:
Hình 4 đúng vì tứ giác này có 4 đỉnh cùng thuộc một đường tròn
Chọn đáp án C
Câu 3: Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF.Bx của nửa kia đường tròn (O) ( với F là tiếp điểm ). Tia AF cắt tia Bx của nửa đường tròn tại D. Khi đó tứ giác OBDF là :
A. Hình thang
B. Tứ giác nội tiếp
C. Hình thang cân
D. Hình bình hành
Lời giải:
Ta có:
Nên nội tiếp được trong một đường tròn
Chọn đáp án B
Câu 4: Tứ giác ABCD nội tiếp đường tròn có hai cạnh đối AB và CD cắt nhau tại M và 
A. 110°
B. 30°
C. 70°
D. 55°
Tứ giác ABCD nội tiếp nên có :
Chọn đáp án C
Câu 5: Cho tam giác ABC có 2 đường cao BD và CE cắt nhau tại H. Tứ giác nào sau đây là tứ giác nội tiếp
A. AHBC
B. BCDE
C. BCDA
D. Không có tứ giác nội tiếp
Ta có: BD và CE là đường cao của tam giác ABC nên 
Trên cùng 1 nửa mặt phẳng bờ BC, hai điểm D và E cùng nhìn đoạn thẳng BC dưới 1 góc vuông nên 4 điểm B, C, D, E cùng thuộc 1 đường tròn hay tứ giác BCDE là tứ giác nội tiếp .
Chọn đáp án B.
Câu 6: Cho đường tròn (O) có AB là đường kính. Trên đường thẳng AB lấy điểm C nằm ngoài đường tròn. Lấy điểm M bất kì nằm trên đường tròn (O). Gọi P là giao điểm của MB và đường vuông góc với AB tại C. Chọn khẳng định đúng.
A. Tứ giác PMAC là tứ giác nội tiếp
B. Tam giác BCM vuông
C. Tam giác BCP có CM là đường trung tuyến.
D. Tất cả sai
Ta có:
Do đó, tứ giác PMAC là tứ giác nội tiếp
Chọn đáp án A.
Câu 7: Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E (khác với điểm A). Tiếp tuyến kẻ từ điểm E cắt các tiếp tuyến kẻ từ điểm A và B của nửa đường tròn (O) lần lượt tại C và D. Gọi M là tiếp điểm của tiếp tuyến kẻ từ điểm E. Tìm khẳng định sai
A. Tứ giác OACM là tứ giác nội tiếp.
B. Tứ giác OBDM là tứ giác nội tiếp
C. Tứ giác ACDB là hình thang vuông
D. Tứ giác ACDO là tứ giác nội tiếp
Suy ra OMDB là tứ giác nội tiếp.
Chọn đáp án D.
Câu 8: Cho nửa đường tròn (O) đường kính AB, trên nửa đường tròn lấy điểm C (C không trùng với A, B). Gọi H là hình chiếu của C trên đường thẳng AB. Trên cung CB lấy điểm D (D khác C, B), Hai đường thẳng AD và CH cắt nhau tại E. . Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B. Đường tròn (O’) cắt CB tại F khác B. Chọn khẳng định sai ?
A. Tứ giác BDEH nội tiếp
B. AC2 = AE.AD
C. EF // AB.
D. Có 2 phương án sai .
* Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B.
Đường tròn (O’) cắt CB tại F khác B. Chứng minh EF // AB.
Ta có:
Hai góc ở vị trí đồng vị ⇒ EF//AB
Chọn đáp án D.
Câu 9: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là giao điểm hai đường cao BD và CE của tam giác ABC (D ∈ AC, E ∈ AB). ) Đường thẳng AO cắt ED và BD lần lượt tại K và M. Tìm khẳng định đúng nhất?
A. Tứ giác ADHE nội tiếp trong một đường tròn.
B. AK.AM = AD2
C. 
D.Tất cả đúng
* Chứng minh tứ giác ADHE nội tiếp trong một đường tròn.
Trong nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia tiếp tuyến Ax với đường tròn (O)
Chọn đáp án D.
Câu 10: Cho tam giác ABC (AB < AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. M là trung điểm của BC. Tìm khẳng định sai ?
A. Tứ giác ABHF nội tiếp
B. Tứ giác BMFO nội tiếp.
C. HE // BD
D. Có ít nhất một khẳng định sai
* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
Và chúng ở vị trí so le trong suy ra: HE // BD
Chọn đáp án D.
Câu 11: Cho hình vẽ dưới đây:
Khi đó mệnh đề đúng là:
Lại có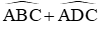 
= 180o (3) (hai góc đối diện của tứ giác nội tiếp)
Từ (1), (2) và (3) ta nhận được (x + 40o) + (x + 20o) = 180o ⇒ x = 60o
Từ (1) ta có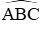 
= 60o + 40o = 100o
Đáp án cần chọn là: C
Câu 13: Cho ∆ABC cân tại A có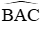 
= 120o. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy D sao cho BCD là tam giác đều. Khi đó:
A. ∆ACD cân
B. ABDC nội tiếp
C. ABDC là hình thang
D. ABDC là hình vuông
Ta có ∆BCD là tam giác đều nên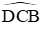 
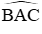
= 60o (1). Mặt khác ∆ABC là tam giác cân tại A có 
= 120o hơn nữa tổng ba góc trong một tam giác bằng 180o nên ta nhận được:
Vậy tứ giác ABDC là tứ giác nội tiếp
Đáp án cần chọn là: B
Câu 14: Cho ∆ABC cân tại A có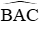 
= 130o. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, kẻ Bx ⊥ BA; Cy ⊥ CA, Bx và Cy cắt nhau tại D. Chọn đáp án sai:
Theo đề bài ta có:
mà hai góc 
lại ở vị trí đối nhau nên tứ giác ABDC là tứ giác nội tiếp nên đáp án B đúng.
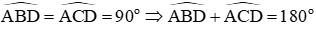
Từ đó suy ra tam giác BCD cân tại D nên đáp án A đúng.
+) Xét tứ giác ABDC nội tiếp nên:
Ta chưa đủ điều kiện để suy ra tứ giác ABDC là hình thoi nên C sai
Đáp án cần chọn là: C
Câu 15: Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm thuộc cung nhỏ AC (cung CM < cung AM). Vẽ MH vuông góc với BC tại Hm vẽ MI vuông góc với AC tại I. Chọn câu đúng:
A. MIHC là hình chữ nhật
B. MIHC là hình vuông
C. MIHC không là tứ giác nội tiếp
D. MIHC là tứ giác nội tiếp
Xét tứ giác IMHC ta có:
tứ giác IMHC nội tiếp (dấu hiệu nhận biết)
Và tứ giác IMHC chưa đủ điều kiện để là hình chữ nhật và hình vuông
Đáp án cần chọn là: D
II. Bài tập tự luận có lời giải
Câu 1: Tính số đo các góc của tứ giác ABCD
Lời giải:
Câu 2: Cho hình vẽ sau.Tính số đo các góc của tứ giác ABCD, biết 
Lời giải:
III. Bài tập vận dụng
Câu 1: Tam giác ABC nội tiếp đường tròn (O; R) có AB = 8cm, AC = 15cm, đường cao AH = 5cm (H nằm ngoài cạnh BC). Tính bán kính của đường tròn.
Câu 2: Dựa vào hình vẽ, tính các góc của tứ giác ABCD
B. Lý thuyết Tứ giác nội tiếp
1. Khái niệm về tứ giác nội tiếp
Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).
Ví dụ 1. Bốn điểm A, B, C, D cùng nằm trên đường tròn (O) như hình vẽ.
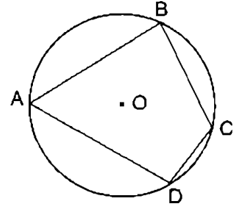
Do đó, ta gọi tứ giác ABCD là tứ giác nội tiếp.
Ví dụ 2. Bốn điểm M, N, P, Q không cùng nằm trên đường tròn (I) như hình vẽ.
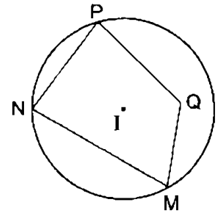
Do đó, ta gọi tứ giác MNPQ không là tứ giác nội tiếp.
2. Định lí
Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.
Ví dụ 3. Cho tứ giác ABCD nội tiếp đường tròn (O). Chứng minh .
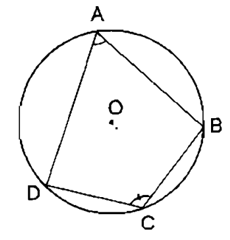
Lời giải:
Theo tính chất góc nội tiếp chắn cung, ta có:
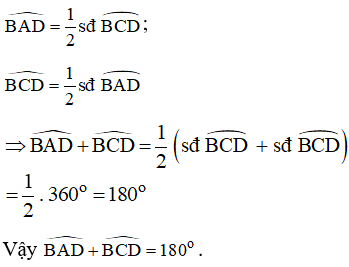
3. Định lí đảo
Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.
Ví dụ 4. Cho tứ giác ABCD có .
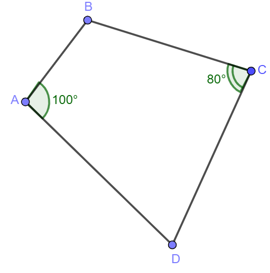
Khi đó, tứ giác ABCD có .
Do đó tứ giác ABCD nội tiếp đường tròn.
4. Dấu hiệu nhận biết tứ giác nội tiếp
- Tứ giác có tổng hai góc đối bằng 180°.
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
- Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.
- Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.
- Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.
Ví dụ 5. Tứ giác ABCD có , góc ngoài của tam giác tại đỉnh A có số đo bằng 80o.
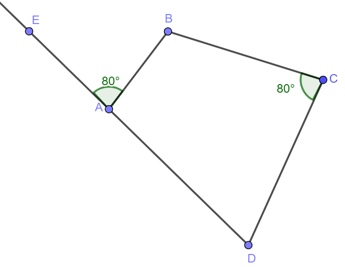
Xét tứ giác ABCD có:
+ và là hai góc đối diện.
+ Góc ngoài đỉnh A và góc trong đỉnh C có tổng số đo bằng 180o.
Do đó tứ giác ABCD nội tiếp đường tròn.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
