Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9 Bài 1: Góc ở tâm - Số đo cung chọn lọc, có đáp án. Tài liệu có 18 trang gồm 30 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Toán 9 Bài 1 có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.

Giới thiệu về tài liệu:

- Số trang: 18 trang

- Số câu hỏi trắc nghiệm: 30 câu

- Lời giải & đáp án: có

Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Góc ở tâm - Số đo cung có đáp án – Toán lớp 9:

Góc ở tâm - Số đo cung

Câu 1: Chọn khẳng định đúng. Góc ở tâm là góc:

A. Có đỉnh nằm trên đường tròn

B. Có đỉnh trùng với tâm đường tròn

C. Có hai cạnh là hai đường kính của đường tròn

D. Có đỉnh nằm trên bán kính của đường tròn

Lời giải:

Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm

Đáp án cần chọn là: B

Câu 2: Chọn khẳng định đúng. Góc có đỉnh trùng với tâm đường tròn được gọi là:

A. Góc ở tâm                                    

B. Góc tạo bởi hai bán kính

C. Góc bên ngoài đường tròn            

D. Góc bên trong đường tròn

Lời giải:

Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.

Đáp án cần chọn là: A

Câu 3: Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng:

A. Số đo cung lớn                             

B. Số đo của hóc ở tâm chắn cung đó

C. Số đo của góc ở tâm chắn cung lớn

D. Số đo của cung nửa đường tròn

Lời giải:

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó

Đáp án cần chọn là: B

Câu 4: Chọn khẳng định đúng. Trong một đường tròn, số đo cung lớn bằng:

A. Số đo cung nhỏ

B. Hiệu giữa 360^o và số đo của cung nhỏ (có chung 2 mút với cung lớn)

C. Tổng giữa 360^o và số đo của cung nhỏ (có chung 2 mút với cung lớn)

D. Số đo của cung nửa đường tròn

Lời giải:

Số đo của cung lớn bằng hiệu giữa 360^o và số đo của cung nhỏ (có chung 2 mút với cung lớn)

Đáp án cần chọn là: B

Câu 5: Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn?

A. Có số đo lớn hơn                          

B. Có số đo nhỏ hơn 90^o

C. Có số đo lớn hơn 90^o                    

D. Có số đo nhỏ hơn

Lời giải:

Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn thì có số đo nhỏ hơn

Đáp án cần chọn là: D

Câu 6: Chọn câu đúng. Trong hai cung của một đường tròn hay hai đường tròn bằng nhau.

A. Hai cung bằng nhau nếu chúng đều là cung nhỏ

B. Hai cung bằng nhau nếu chúng có số đo nhỏ hơn 90^o

C. Hai cung bằng nhau nếu chúng đều là cung lớn

D. Hai cung bằng nhau nếu chúng có số đo bằng nhau

Lời giải:

Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, hai cung bằng nhau nếu chúng có số đo bằng nhau

Đáp án cần chọn là: D

Câu 7: Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M, biết 

Thông hiểu: Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M, biết 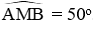. Số đo cung AB nhỏ và số đo cung AB lớn lần lượt là:

A. 130^o; 250^o.

B. 130^o; 230^o.

C. 230^o; 130^o.

D. 150^o; 210^o.

Lời giải:

Vì MA, MB là hai tiếp tuyến của đường tròn (O) nên OM là tia phân giác của ; MO là tia phân giác của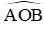 

Mà tam giác OAM vuông tại A (do MA là tiếp tuyến) nên

Đáp án cần chọn là: C

Câu 8: Cho hai tiếp tuyến tại C và D của đường tròn (O) cắt nhau tại N, biết 

Thông hiểu: Cho hai tiếp tuyến tại C và D của đường tròn (O) cắt nhau tại N, biết 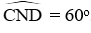. Số đo cung CD nhỏ và số đo cung CD lớn lần lượt là:

A. 150^o; 210^o.

B. 120^o; 230^o.

C. 120^o; 240^o.

D. 240^o; 120^o.

Lời giải:

Vì NC, ND là hai tiếp tuyến của đường tròn nên ON là tia phân giác của ; NO là tia phân giác của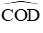 

Mà tam giác ODN vuông tại D (do ND là tiếp tuyến) nên:

Đáp án cần chọn là: D

Câu 9: Cho tam giác ABC đều nội tiếp đường tròn (O). Tính số đo cung AC lớn.

A. 240^o      

B. 120^o       

C. 360^o       

D. 210^o

Lời giải:

Vì tam giác ABC đều có O là tâm đường tròn ngoại tiếp nên O cũng là giao ba đường phân giác nên AO; CO lần lượt là các đường phân giác 

Xét tam giác AOC có 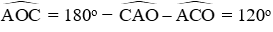 nên số đo cung nhỏ AC là 120^o

Do đó số đo cung lớn AC là 360^o – 120^o = 240^o

Đáp án cần chọn là: A

Câu 10: Cho tam giác ABC đều nội tiếp đường tròn (O). Tính số đo cung BC nhỏ.

A. 240^o      

B. 60^o

C. 180^o       

D. 120^o

Câu 11: Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm). Số đo góc 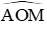 là:

A. 30^o          

B. 120^o       

C. 50^o         

D. 60^o

Lời giải:

Vì tam giác ABC đều có O là tâm đường tròn ngoại tiếp nên O cũng là giao ba đường phân giác nên BO; CO lần lượt là các đường phân giác 

Do đó số đo cung nhỏ BC là 120^o

Đáp án cần chọn là: D

Vận dụng: Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm). Số đo cung AB nhỏ là:

A. 240^o      

B. 120^o       

C. 360^o                

D. 210^o

Câu 12: Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = R√2. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm). Số đo góc 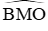 là:

A. 45^o          

B. 30^o         

C. 90^o         

D. 60^o

Lời giải:

Đáp án cần chọn là: A

Vận dụng: Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = R√2. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm). Số đo cung AB lớn là:

A. 270^o      

B. 90^o         

C. 180^o       

D. 210^o

Lời giải:

Xét tam giác OBM vuông tại B (do BM là tiếp tuyến của (O)) có:

Xét đường tròn (O) có MA; MB là hai tiếp tuyến cắt nhau tại M nên OM là tia phân giác của góc 

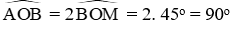
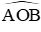
Suy ra  mà  là góc ở tâm chắn cung AB

Nên số đo cung nhỏ AB là 90^o suy ra số đo cung lớn AB là 360^o – 90^o = 270^o

Đáp án cần chọn là: A

Câu 13: Cho (O; R) và dây cung MN = R√3. Kẻ OI vuông góc với MN tại I. Tính độ dài OI theo R

Lời giải:

Xét (O) có OI ⊥ MN tại I nên I là trung điểm của dây MN (đường kính vuông góc với dây thì đi qua trung điểm của dây đó) 

Xét tam giác OIM vuông tại I, theo định lý Pytago ta có: OI² = OM² – MI²

Đáp án cần chọn là: D

Vận dụng: Cho (O; R) và dây cung MN = R√3. Kẻ OI vuông góc với MN tại I. Tính số đo cung nhỏ MN.

A. 120^o      

B. 150^o       

C. 90^o         

D. 145^o

Lời giải:

Xét tam giác OIM vuông tại I ta có:

∆MON cân tại O có OI vừa là đường cao, vừa là đường phân giác nên:

Đáp án cần chọn là: A

Câu 14: Cho (O; R) và dây cung MN = R√2. Kẻ OI vuông góc với MN tại I. Tính độ dài OI theo R.

Lời giải:

Xét (O) có OI ⊥ MN tại I nên I là trung điểm của MN 

Xét tam giác OIM vuông tại I, theo định lý Pytago ta có: OI² = OM² – MI²

Đáp án cần chọn là: B

Vận dụng: Cho (O; R) và dây cung MN = R√2. Kẻ OI vuông góc với MN tại I. Tính số đo cung nhỏ MN

A. 120^o      

B. 150^o       

C. 90^o         

D. 60^o

Lời giải:

∆MON cân tại O có OI vừa là đường cao vừa là đường phân giác nên:

Suy ra số đo cung nhỏ MN là 90^o

Đáp án cần chọn là: C

Câu 15: Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AB, AC lần lượt tại I, K. So sánh các cung nhỏ BI và cung nhỏ CK

A. Số đo cung nhỏ BI bằng số đo cung nhỏ CK

B. Số đo cung nhỏ BI nhỏ hơn số đo cung nhỏ CK

C. Số đo cung nhỏ BI lớn hơn số đo cung nhỏ CK

D. Số đo cung nhỏ BI bằng hai lần số đo cung nhỏ CK

Lời giải:

Xét các tam giác ∆IBC và ∆KBC có BC là đường kính của (O) và I; K ∈ (O)

Nên ∆IBC vuông tại I và ∆KBC vuông tại K

Xét hai tam giác vuông ∆IBC và ∆KBC ta có BC chung; 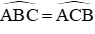 (do ∆ABC cân)

⇒  ∆IBC = ∆KCB (ch – gn) ⇒ IB = CK

Suy ra ∆COK = IOB (c – c − c) 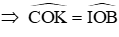 suy ra số đo hai cung nhỏ CK và BI bằng nhau

Đáp án cần chọn là: A

Vận dụng: Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AB, AC lần lượt tại I, K. Tính 

A. 80^o         

B. 100^o       

C. 60^o         

D. 40^o

Câu 16: Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AB, AC lần lượt tại I, K. So sánh các cung nhỏ CI và cung nhỏ BK

A. Số đo cung nhỏ CI bằng hai lần số đo cung nhỏ BK

B. Số đo cung nhỏ CI nhỏ hơn số đo cung nhỏ BK

C. Số đo cung nhỏ BK lớn hơn hơn số đo cung nhỏ CI

D. Số đo cung nhỏ BK bằng số đo cung nhỏ CI

Lời giải:

Xét tam giác ∆IBC và ∆KBC có BC là đường kính của (O) và I; K ∈ (O)

Nên ∆IBC vuông tại I và ∆KBC vuông tại K

Xét hai tam giác vuông ∆IBC và ∆KBC ta có BC chung; 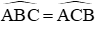 (do ∆ABC cân)

⇒  ∆IBC = ∆KCB (ch – gn) ⇒ IC = BK (hai cạnh tương ứng)

Suy ra ∆COI = ∆BOK (c – c – c) 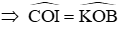 suy ra số đo hai cung nhỏ CI và BK bằng nhau

Đáp án cần chọn là: D

Vận dụng: Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AB, AC lần lượt tại I, K. Tính 

A. 36^o         

B. 144^o       

C. 108^o       

D. 72^o

Lời giải:

Xét tam giác ∆IBC và ∆KBC có BC là đường kính của (O) và I; K ∈ (O)

Nên ∆IBC vuông tại I và ∆KBC vuông tại K

Xét hai tam giác vuông IBC và KBC ta có BC chung; 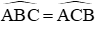 (do ∆ABC cân)

⇒ ∆IBC = ∆KCB (ch – gn) ⇒ IC = BK (hai cạnh tương ứng)

Suy ra ∆COI = ∆BOK (c – c – c) 

Đáp án cần chọn là: C

Câu 17: Cho đường tròn (O; R). Gọi H là trung điểm của bán kính OA, dây CD vuông góc với OA tại H. Tính số đo cung lớn CD

A. 260^o      

B. 300^o       

C. 240^o       

D. 120^o

Lời giải:

Xét đường tròn (O) có OA ⊥ CD tại H nên H là trung điểm của CD

Tứ giác OCAD có hai đường chéo vuông góc và giao nhau tại trung điểm mỗi đường nên OCAD là hình thoi

⇒ OA = CA mà OC = OA nên OC = OA = AC hay tam giác OAC đều

Do đó số đo cung nhỏ CD là 120^o và số đo cung lớn CD là 360^o – 120^o = 240^o

Đáp án cần chọn là: C

Câu 18: Cho đường tròn (O; R). Gọi H là điểm thuộc bán kính OA sao cho 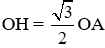. Dây CD vuông góc với OA tại H. Tính số đo cung lớn CD

A. 260^o      

B. 300^o       

C. 240^o       

D. 120^o

Lời giải:

Xét đường tròn (O) có OA ⊥ CD tại H nên H là trung điểm của CD

Xét tam giác OHC vuông tại H có:

Mà tam giác OCD cân tại O (OC = OD = R) có OH là đường cao nên OH cũng là đường phân giác, suy ra 

Do đó số đo cung nhỏ CD là 60^o và số đo cung lớn CD là 360^o – 60^o = 300^o

Đáp án cần chọn là: B

Câu 19: Cho đường tròn (O) đường kính AB, vẽ góc ở tâm 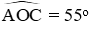. Vẽ dây CD vuông góc với AB và dây DE song song với AB. Tính số đo cung nhỏ BE

A. 55^o         

B. 60^o         

C. 40^o         

D. 50^o

Lời giải:

Xét (O) có CD ⊥ OA; ED // OA ⇒ CD ⊥ ED hay 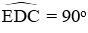 mà E; D; C ∈ (O) nên EC là đường kính của (O) hay E; O; C thẳng hàng

Do đó 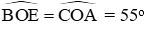 (đối đỉnh) nên số đo cung nhỏ BE là 55^o

Đáp án cần chọn là: A

Câu 20: Cho đường tròn (O) đường kính AB, vẽ góc ở tâm 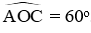. Vẽ dây CD vuông góc với AB và dây DE song song với AB. Tính số đo cung nhỏ BE

A. 120^o                

B. 60^o         

C. 240^o       

D. 30^o

Lời giải:

Xét (O) có CD ⊥ OA; ED // OA ⇒ CD ⊥ ED hay 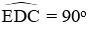 mà E; D; C ∈ (O) nên EC là đường kính của (O) hay E; O; C thẳng hàng

Do đó 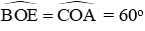 (đối đỉnh) nên số đo cung nhỏ BE là 60^o

Đáp án cần chọn là: B

Bài giảng Toán 9 Bài 1: Góc ở tâm số đo cung