Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Định lý Pi-ta-go trong tam giác vuông Toán lớp 7, tài liệu bao gồm 17 trang, tuyển chọn bài tập Định lý Pi-ta-go trong tam giác vuông đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Định lý Pi-ta-go trong tam giác vuông gồm các nội dung chính sau:

A. Phương pháp giải

- tóm tắt lý thuyết ngắn gọn.

B. Một số ví dụ

- gồm 8 ví dụ minh họa đa dạng của các dạng bài tập Định lý Pi-ta-go trong tam giác vuông có lời giải chi tiết.

C. Bài tập vận dụng

- gồm 14 bài tập vận dụng giúp học sinh tự rèn luyện cách giải các dạng bài tập Định lý Pi-ta-go trong tam giác vuông.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

ĐỊNH LÝ PY-TA-GO TRONG TAM GIÁC VUÔNG

A. Phương pháp giải

Trong toán học, định lý Py-ta-go là một liên hệ trong hình học phẳng giữa ba cạnh tam giác của một tam giác vuông.

- Pythagoras (tiếng Hy Lạp: Πυθαγόρας; sinh khoảng năm 580 đến 572 TCN - mất khoảng năm 500 đến 490 TCN) là một nhà triết học người Hy Lạp và là người sáng lập ra phong trào tín ngưỡng có tên học thuyết Pythagoras. Ông thường được biết đến như một nhà khoa học và toán học vĩ đại. Trong tiếng Việt, tên của ông thường được phiên âm từ tiếng Pháp (Pythagore) thành Py-ta-go.

- Pythagoras đã thành công trong việc chứng minh tổng 3 góc của một tam giác bằng 180° và nổi tiếng nhất nhờ định lý toán học mang tên ông. Ông cũng được biết đến là "cha đẻ của số học". Ông đã có nhiều đóng góp quan trọng cho triết học và tín ngưỡng vào cuối thế kỷ 7 TCN. Về cuộc đời và sự nghiệp của ông, có quá nhiều các huyền thoại khiến việc tìm lại sự thật lịch sử không dễ dàng. Pythagoras và các học trò của ông tin rằng mọi sự vật đều liên hệ đến toán học, và mọi sự việc đều có thể tiên đoán trước qua các chu kỳ.

1) Định lí Py-ta-go

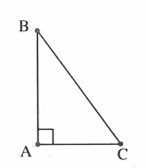
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

$\Delta ABC$ vuông tại $A\Rightarrow B{C}^2=A{B}^2+A{C}^2$.

2) Định lí Py-ta-go đảo

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

$\Delta ABC:B{C}^2=A{B}^2+A{C}^2\Rightarrow \widehat{BAC}=90°$.

B. Một số ví dụ

Ví dụ 1: Cho hình vẽ sau. Tìm x:

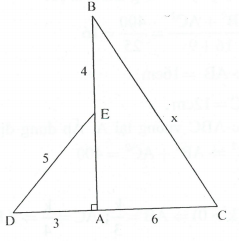
Giải

* Tìm cách giải. Trong một tam giác vuông nếu biết độ dài hai cạnh thì tìm được độ dài cạnh thứ ba.

Xét $\Delta ADE$ ta tính được AE từ đó xét $\Delta ABC$, tính được BC.

* Trình bày lời giải.

Tam giác ADE vuông tại A. Áp dụng định lý Py-ta-go, ta có:

$A{D}^2+A{E}^2=D{E}^2\Rightarrow 3^2+A{E}^2=5^2\Rightarrow AE=4$.

Từ đó suy ra $AB=8$.

Tam giác ABC vuông tại A. Áp dụng định lý Py-ta-go, ta có:

$A{B}^2+A{C}^2=B{C}^2\Rightarrow 8^2+6^2=B{C}^2\Rightarrow BC=10$.

Ví dụ 2: Cho tam giác ABC vuông tại A. Biết $3AB=4AC$ và $BC=20\text{cm}$.

Tính độ dài các cạnh AB và AC.

Giải

* Tìm cách giải. Bài toán biết độ dài cạnh huyền tam giác vuông, tính độ dài hai cạnh góc vuông của tam giác ấy, tất yếu suy nghĩ tới việc dùng định lý Py-ta-go.

Bài toán cho $3AB=4AC$. Khai thác yếu tố này, chúng ta có thể giải bài toán theo ba cách:

Ví dụ 3: Hãy chỉ ra bộ ba đoạn thẳng nào sau đây có thể là số đo ba cạnh của một tam giác? Có giải thích?

a) 4cm, 2cm, 6cm. 

b) 4cm, 3cm, 6cm.   

c) 4cm, 1cm, 6cm.

Ví dụ 4: Tính chu vi của một tam giác cân biết hai cạnh bằng 4m và 9m.

Ví dụ 5: Cho $\Delta ABC$ cân tại A, đường cao AH. Biết $AB=5cm,BC=6cm.$ Tính độ dài các đoạn thẳng BH, AH ?