Cho đường thẳng ∆ và hai điểm A, B, sao cho ∆ không phải là đường trung trực của đoạn thẳng AB

Van Anh Ngày: 26-06-2023 Lớp 11

466

Với giải Luyện tập 3 trang 15 Chuyên đề Toán 11 Kết nối tri thức chi tiết trong Bài 3: Phép đối xứng trục giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:

Giải Chuyên đề Toán 11 Bài 3: Phép đối xứng trục

Luyện tập 3 trang 15 Chuyên đề Toán 11: Cho đường thẳng ∆ và hai điểm A, B, sao cho ∆ không phải là đường trung trực của đoạn thẳng AB. Điểm M thay đổi trên ∆ (M không thuộc đường thẳng AB). Gọi M' là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thẳng cố định.

Lời giải:

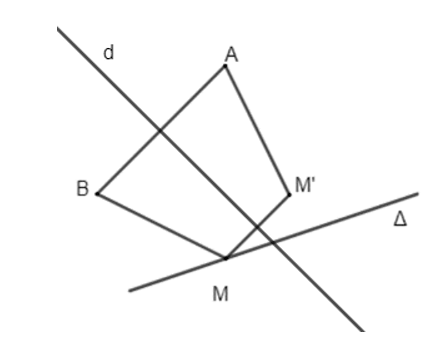
Luyện tập 3 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức

Gọi d là đường trung trực của đoạn thẳng AB. Vì AB cố định nên d cố định.

Do A, B, M, M' là 4 đỉnh của hình thang cân nhận AB là một cạnh đáy nên MM' là đáy còn lại của hình thang cân và đường trung trực d của đoạn thẳng AB cũng là đường trung trực của đoạn thẳng MM'. Do đó M' là ảnh của điểm M qua phép đối xứng trục d.

Mặt khác, M thuộc đường thẳng ∆ nên M' thuộc đường thẳng ∆' là ảnh của đường thẳng ∆ qua phép đối xứng trục d.

Vậy rằng M' thay đổi trên một đường thẳng cố định ∆' là ảnh của đường thẳng ∆ qua phép đối xứng trục d.

Xem thêm lời giải bài tập Chuyên đề học tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

HĐ1 trang 12 Chuyên đề Toán 11: Cầu Ponte Sisto in hình dưới dòng sông Tiber, tạo nên một hình ảnh có tính đối xứng trục....

Luyện tập 1 trang 13 Chuyên đề Toán 11: Xét mặt phẳng tọa độ Oxy (H.1.15). Trong các khẳng định sau, chọn các khẳng định đúng....

HĐ2 trang 14 Chuyên đề Toán 11: Cho phép đối xứng trục d biến M thành M', N thành N'. Xét hệ trục tọa độ Oxy sao cho trục Oy trùng với d (H.1.16a). Giả sử M có tọa độ là (x₁; y₁), N có tọa độ là (x₂; y₂).....

Luyện tập 2 trang 14 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y – 1 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép đối xứng trục Ox....

Vận dụng trang 15 Chuyên đề Toán 11: Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng....

Bài 1.6 trang 15 Chuyên đề Toán 11: Cho hai điểm phân biệt A và B. Xác định phép đối xứng trục biến điểm A thành điểm B....

Bài 1.7 trang 15 Chuyên đề Toán 11: Cho hai đường tròn không đồng tâm, những có cùng bán kính (O₁; R) và (O₂; R). Xác định phép đối xứng trục biến (O₁; R) thành (O₂; R)....

Bài 1.8 trang 15 Chuyên đề Toán 11: Cho đường thẳng d và hai điểm phân biệt A, B sao cho đường thẳng AB không vuông góc với d. Gọi M, N tương ứng là các điểm đối xứng với A, B qua d. Hỏi A, B, M, N có là 4 đỉnh của một hình thang cân hay không?....

Bài 1.9 trang 15 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho ∆: x + 2y – 1 = 0. Viết phương trình đường thẳng d đối xứng với ∆ qua trục Ox.....