Với tóm tắt lý thuyết Toán lớp 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 8.
Lý thuyết Toán lớp 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
A. Lý thuyết Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
1. Đồ thị của hàm số bậc nhất
Đồ thị của hàm số y = ax + b (a0) là một đường thẳng.
Chú ý: Đồ thị hàm số y = ax + b (a0) còn gọi là đường thẳng y = ax + b (a0).
Ví dụ: Cho hàm số y = 2x – 3 có hai điểm A(1, -1) và B(2; 1) thuộc đồ thị của hàm số y = 2x – 3.
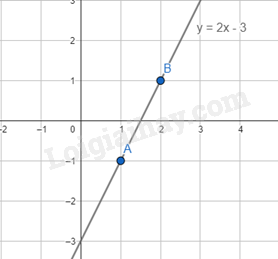
2. Vẽ đồ thị của hàm số bậc nhất
Hàm số y = ax (a0)
Để vẽ đồ thị của hàm số y = ax (a0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.
Hàm số y = ax + b (a0)
Để vẽ đồ thị của hàm số y = ax + b (a0, b0), ta có thể xác định hai điểm P(0; b) và Q rồi vẽ dường thẳng đi qua hai điểm đó.
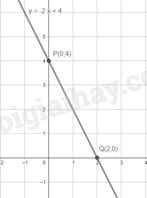
Ví dụ: Cho hàm số y = -2x + 4
Với x = 0 thì y = 4, ta được điểm P(0;4)
Với y = 0 thì x = 22, ta được điểm Q(2;0)
Vậy đồ thị hàm số y = -2x + 4 là đường thẳng đi qua hai điểm P(0;4) và Q(2;0)
3. Hệ số góc của đường thẳng y = ax + b (a0)
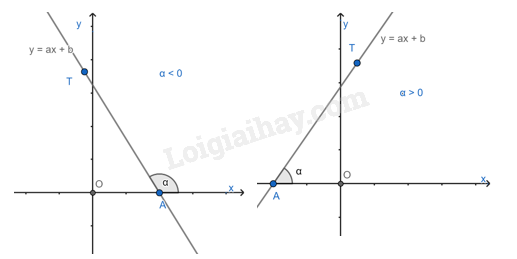
Góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.
Góc tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc )
Hệ số góc
Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a0).
Nhận xét:
Khi hệ số góc a > 0 thì góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.
Khi hệ số góc a < 0 thì góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.
Ứng dụng của hệ số góc
Cho d: y = ax + b (a0) và d’: y = a’x + b’ (a’0)
a. d // d’ a = a’, b b’.
b.
c. d cắt d’ a a’
Ví dụ: y = 2x + 1, y = 2x + 3 là hai đường thẳng song song vì có hệ số góc bằng nhau và hệ số tự do khác nhau.
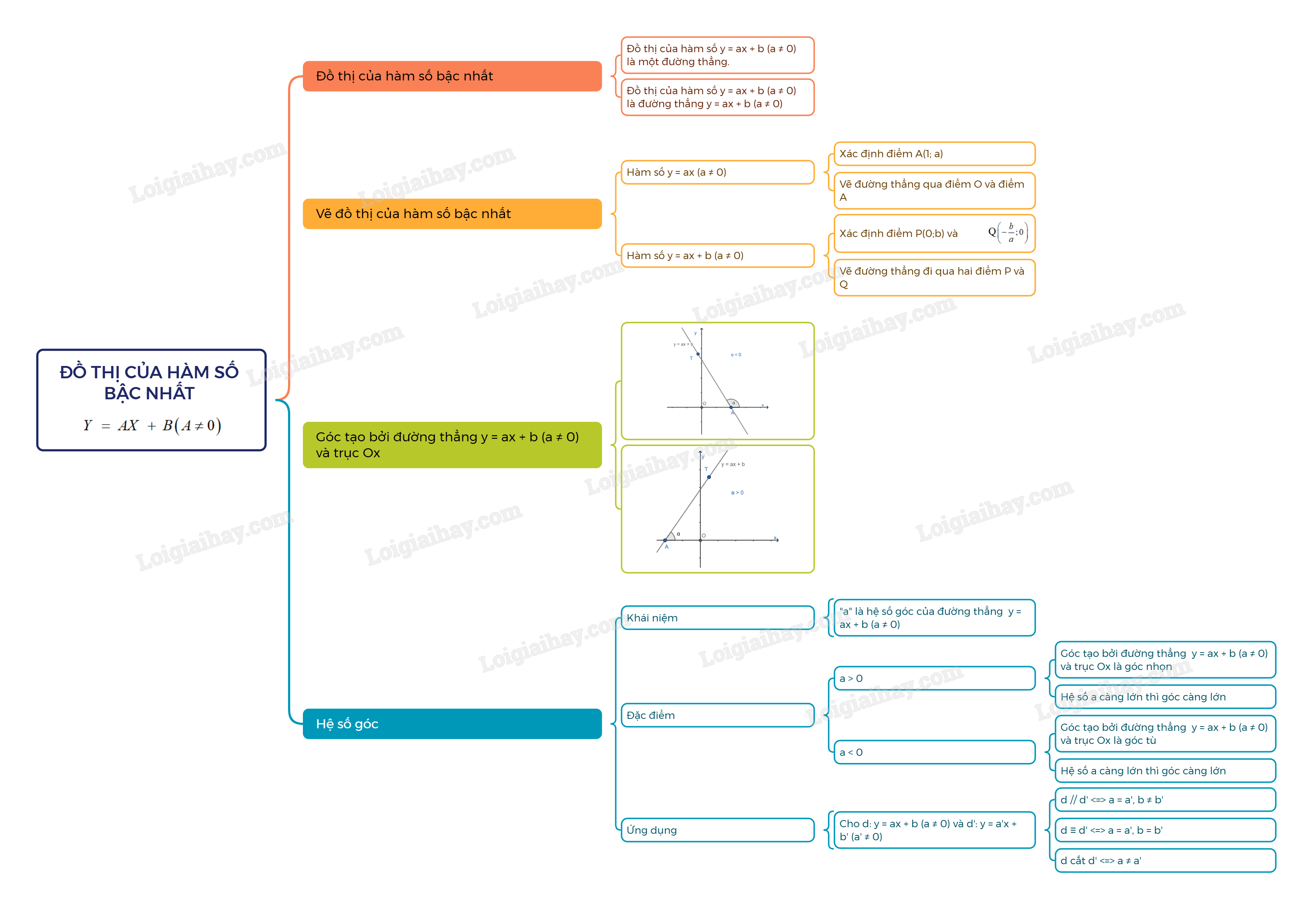
Sơ đồ tư duy Đồ thị của hàm số bậc nhất.
B. Bài tập Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
Bài 1: Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong các đường thẳng sau: y = 3x + 1; y = 3x; y = −2x – 2.
Hướng dẫn giải
Cặp đường thẳng song song là: y = 3x + 1; y = 3x.
Cặp đường thẳng cắt nhau là: y = 3x + 1 và y = −2x – 2; y = 3x và y = −2x – 2.
Bài 2: Vẽ đồ thị của các hàm số y = 3x; y = −x − 2 trên cùng một mặt phẳng tọa độ?
Hướng dẫn giải
+ Với x = 1 thì y = 3, ta được điểm A(1; 3) thuộc đồ thị hàm số y = 3x.
Vẽ đồ thị hàm số y = 3x là đường thẳng đi qua gốc tọa độ và điểm A.
+ Với x = 0 thì y = −2, ta được điểm P(0; −2) thuộc đồ thị hàm số y = −x − 2.
Với y = 0 thì x = −2, ta được điểm Q(−2; 0) thuộc đồ thị hàm số y = −x − 2.
Vẽ đồ thị hàm số y = −x – 2 là đường thẳng đi qua hai điểm P và Q.
Bài 3: a) Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 và đi qua điểm M(1; 2)?
b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x?
Hướng dẫn giải
a) Vì đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 nên đường thẳng có dạng y = - x + b
y = −x + b.
Vì đường thẳng y = −x + b đi qua điểm M(1; 2) nên ta có: 2 = −1 + b b = 3.
Vậy y = −x + 3.
b) Vì đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x nên đường thẳng có dạng: y = 2x + b.
Mà đường thẳng y = 2x + b đi qua điểm M(1; 3) nên 3 = 2.1 + b b = 1.
Vậy y = 2x +1.
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
Lý thuyết Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
Lý thuyết Bài 1: Hình chóp tam giác đều
Lý thuyết Bài 2: Hình chóp tứ giác đều
Lý thuyết Bài 1: Định lí Pythagore