Với tóm tắt lý thuyết Toán lớp 8 Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 8.

Lý thuyết Toán lớp 8 Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

A. Lý thuyết Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

1. Hằng đẳng thức:

Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.

Ví dụ: $a+b=b+a;a(a+2)=a^2+2a$ là những hằng đẳng thức.

$a^2-1=3a;a(a-1)=2a$ không phải là những hằng đẳng thức.

2. Hiệu hai bình phương

Hiệu hai bình phương là gì?

$A^2-B^2=(A-B)(A+B)$

Ví dụ: ${101}^2-{99}^2=(101-99)(101+99)=2.200=400$

3. Bình phương của một tổng:

${\left(A+B\right)}^2=A^2+2AB+B^2$

Ví dụ: ${101}^2=(100+1{)}^2={100}^2+\mathrm{2.100.1}+1^2=10201$

4. Bình phương của một hiệu:

${\left(A-B\right)}^2=A^2-2AB+B^2$

Ví dụ: ${99}^2=(100-1{)}^2={100}^2-\mathrm{2.100.1}+1^2=9801$

Sơ đồ tư duy Hiệu hai bình phương. Bình phương của một tổng hay một hiệu 

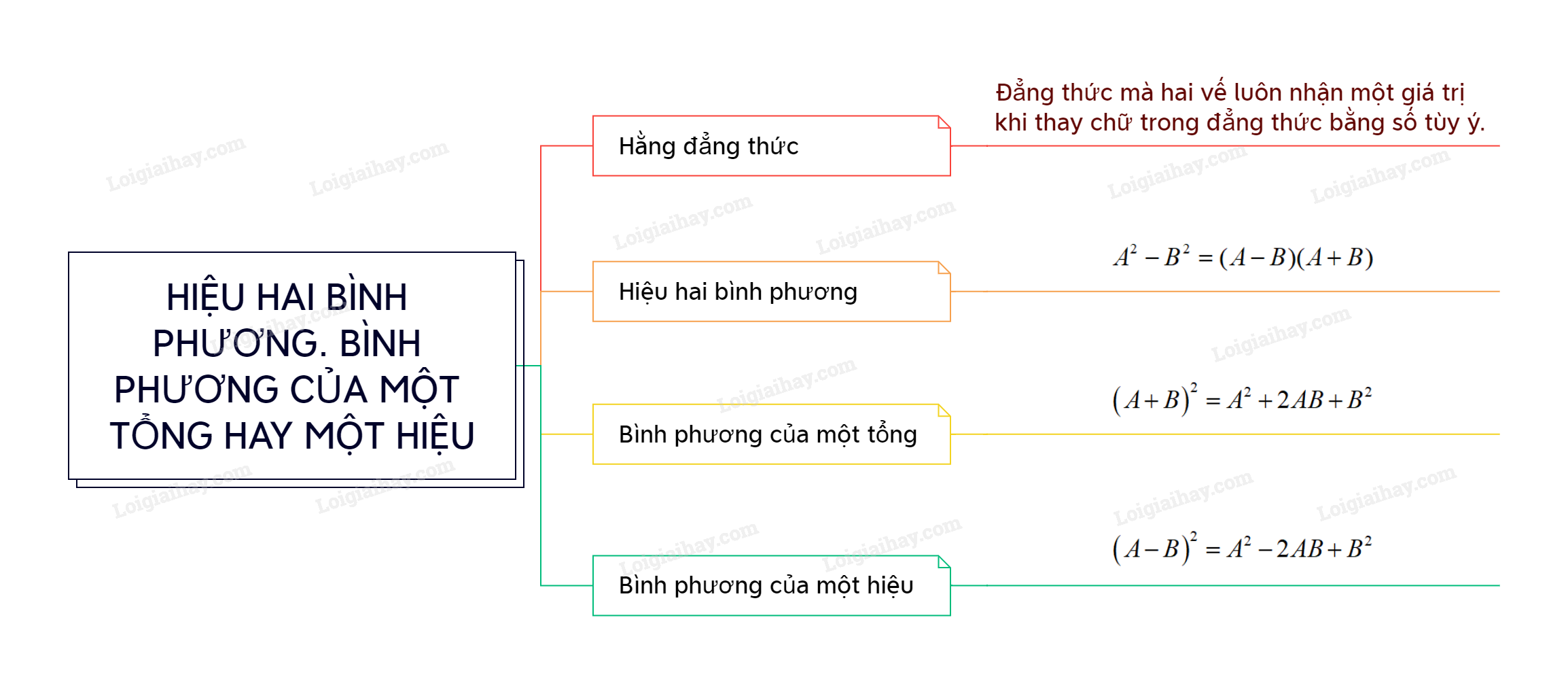
B. Bài tập Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

Bài 1. Những đẳng thức nào sau đây là hằng đẳng thức?

a) 2x + 1 = x + 5;                                       

b) x(x + 1) =x² + x;

c) 4a(a – 1) = 4a² – 4a;                               

d) 2a + b = 2b + a.

Hướng dẫn giải

a) Đẳng thức 2x + 1 = x + 5 không là hằng đẳng thức vì khi ta thay x = 2 thì hai vế của đẳng thức không bằng nhau.

b) Đẳng thức x(x + 1) =x² + x là hằng đẳng thức.

c) Đẳng thức 4a(a – 1) = 4a² – 4a là hằng đẳng thức.

d) Đẳng thức 2a + b = 2b + a không là hằng đẳng thức vì khi ta thay a = 1, b = 5 thì hai vế của đẳng thức không bằng nhau.

Bài 2. Thay dấu ? bằng biểu thức thích hợp.

a) (2x – y)(2x + y) = ? – y²;

b) (x + 5y)(x – 5y) = x² – ? y²;

c) x² + ? xy + 4y² = (x + 2y)²;

d) (? + 3)² = 4x² + ? + 9.

Hướng dẫn giải

a) (2x – y )( 2x + y) = (2x)² – y² = 4x² – y²;

b) (x + 5y)(x – 5y) = x² – (5y)² = x² – 25y²;

c) x² + 4xy + 4y² = x² + 2 . x . 2y + (2y)² = (x + 2y)²;

d) (2x + 3)² = (2x)² + 2 . 2x . 3 + 3² = 4x² + 12x + 9.

Bài 3. Rút gọn biểu thức sau:

a) (2x – 1)² – (2x + 1)²;                              

b) (3x + 2y)² + (2x – 3y)².

Hướng dẫn giải

a) (2x – 1)² – (2x + 1)²

= [(2x – 1) – (2x + 1)][(2x – 1) + (2x + 1)]

= –2.4x

= –8x.

b) (3x + 2y)² + (2x – 3y)²

= (3x)² + 2.3x.2y + (2y)² + (2x)² – 2.2x.3y + (3y)²

= 9x² + 12xy + 4y² + 4x² –12xy + 9y²

= 13x² + 13y².

Bài 4. Chứng minh rằng với mọi số tự nhiên ta có:

(n + 2)² – n² chia hết cho 4.

Hướng dẫn giải

Ta có: (n + 2)² – n² = n² + 4n + 4 – n² = 4n + 4 = 4(n + 1)

Vì 4 ⁝ 4 suy ra 4(n + 1) ⁝ 4 với mọi số tự nhiên n.

Vậy (n + 2)² – n² chia hết cho 4 với mọi số tự nhiên n.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 5: Phép chia đa thức cho đơn thức