Với giải Hoạt động khám phá 1 trang 64 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Giới hạn của dãy số  giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 1: Giới hạn của dãy số

Hoạt động khám phá 1 trang 64 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{{\left(-1\right)}^n}{n}$.

a) Tìm các giá trị còn thiếu trong bảng sau:

b) Với n như thế nào thì |u_n| bé hơn 0,01; 0,001?

c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm u_n đến điểm 0 khi n trở lên rất lớn?

Lời giải:

a) Ta có:

Với n = 100 có |u₁₀₀| = 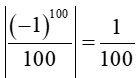 = 0,01.

Với n = 1 000 có |u₁₀₀₀| = 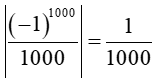 = 0,001.

Khi đó ta có bảng:

b) Với n > 100 thì |u_n| < 0,01.

Với n > 1000 thì |u_n| < 0,001.

c) Khi n trở nên rất lớn thì khoảng cách từ điểm u_n đến điểm 0 càng nhỏ.

 Lý thuyết Giới hạn hữu hạn của dãy số

a, Giới hạn 0 của dãy số

- Dãy số $\left(u_n\right)$ có giới hạn 0 khi n dần tới dương vô cực, nếu $\left|u_n\right|$ có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.

 Kí hiệu $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=0$ hay $u_n\to 0$khi  $n\to +\mathrm{\infty }$ hay $lim{u}_n=0$.

* Chú ý:

+ $lim\frac{1}{n^k}=0,k\in \mathbb{Z}.$

+ Nếu $\left|q\right|<1$ thì $lim{q}^n=0$

b, Giới hạn hữu hạn của dãy số

Ta nói dãy số $\left(u_n\right)$ có giới hạn là số thực a khi n dần tới dương vô cực, nếu $\underset{n\to +\mathrm{\infty }}{lim}\left(u_n-a\right)=0$, kí hiệu $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=a$ hay $u_n\to a$ khi  $n\to +\mathrm{\infty }$.

* Chú ý:  Nếu $u_n=c$(c là hằng số) thì $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=c$