Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm chi tiết sách Toán 11 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm
Lời giải:
Ta có bảng thống kê sau:
|
Độ tuổi |
[20; 30) |
[30; 40) |
[40; 50) |
[50; 60) |
[60; 70) |
|
Khách hàng nam |
4 |
6 |
10 |
7 |
3 |
|
Khách hàng nữ |
3 |
9 |
6 |
3 |
2 |
Sau bài học này, ta tính số tuổi trung bình của khách hàng nam và nữ như sau:
Độ tuổi trung bình của khách hàng nam là:
.
Độ tuổi trung bình của khách hàng nữ là:
.
1. Số liệu ghép nhóm
Lời giải:
Ta có bảng sau:
|
Khoảng tuổi |
[20; 30) |
[30; 40) |
[40; 50) |
[50; 60) |
[60; 70) |
|
Số khách hàng nữ |
3 |
9 |
6 |
3 |
2 |
Hãy chia mẫu số liệu trên thành 5 nhóm, lập bảng tần số ghép nhóm, hiệu chỉnh bảng tần số ghép nhóm và xác định giá trị đại diện cho mỗi nhóm.
Lời giải:
Khoảng biến thiên của mẫu số liệu trên là: R = 29 – 10 = 19.
Độ dài mỗi nhóm L > .
Chọn L = 4 và chia các dữ liệu thành các nhóm [45; 49), [49; 53), [53; 57), [57; 61), [61; 65).
Khi đó ta có bảng tần số ghép nhóm sau:
|
Số ba lô đã bán |
[10; 14) |
[14; 18) |
[18; 22) |
[22; 26) |
[26; 30) |
|
Giá trị đại diện |
12 |
16 |
20 |
24 |
28 |
|
Số ngày |
8 |
5 |
8 |
3 |
6 |
2. Số trung bình
a) Tính giá trị đại diện ci, 1 ≤ i ≤ 5, của từng nhóm số liệu.
b) Tính n1c1 + n2c2 + n3c3 + n4c4 + n5c5.
c) Tính .
Lời giải:
a) Ta có bảng sau:
|
Số câu trả lời đúng |
[16; 21) |
[21; 26) |
[26; 31) |
[31; 36) |
[36; 41) |
|
Giá trị đại diện |
18,5 |
23,5 |
28,5 |
33,5 |
38,5 |
|
Số học sinh |
4 |
6 |
8 |
18 |
4 |
b) Ta có:
n1c1 + n2c2 + n3c3 + n4c4 + n5c5 = 18,5.4 + 23,5.6 + 28,5.8 + 33,5.18 + 38,5.4 = 1 200.
c) Ta có: .
Lời giải:
Ước lượng trung bình số câu trả lời đúng của các học sinh lớp 11A1 là:
(câu hỏi).
Lời giải:
Ta có bảng ghép nhóm sau:
Cân nặng trung bình của học sinh xấp xỉ là:
(kg).
Cân nặng trung bình của mẫu số liệu gốc là:
(kg).
Ta thấy giá trị cân nặng trung bình ước lượng gần bằng giá trị cân nặng trung bình của mẫu số liệu gốc.
3. Mốt
Lời giải:
Ta có bảng thống kê sau:
|
Độ tuổi |
[20; 30) |
[30; 40) |
[40; 50) |
[50; 60) |
[60; 70) |
|
Khách hàng nam |
4 |
6 |
10 |
7 |
3 |
|
Khách hàng nữ |
3 |
9 |
6 |
3 |
2 |
Dựa vào bảng số liệu trên ta thấy:
Đối với nam: Độ tuổi từ 40 đến 50 mua bảo hiểm nhiều nhất.
Đối với nữ: Độ tuổi từ 30 đến 40 mua bảo hiểm nhiều nhất.
Ta có thể biết được mốt của mẫu số liệu bằng cách như sau:
Đối với nam, mốt của mẫu số liệu là:
(tuổi).
Đối với nữ, mốt của mẫu số liệu là:
(tuổi).
Lời giải:
Dựa vào bảng dữ liệu ta thấy:
Đối với nam ở độ tuổi từ 40 đến 50 có nhu cầu mua bảo hiểm lớn nhất đặc biệt là độ tuổi 46.
Đối với nữ ở độ tuổi từ 30 đến 40 có nhu cầu mua bảo hiểm nhiếu nhất đặc biệt là độ tuổi 37.
Bài tập
a) Tính cự li trung bình của mỗi lần ném.
b) Tổng hợp lại kết quả ném của anh Văn vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng cự li trung bình mỗi lần ném từ bảng tần số ghép nhóm trên.
d) Khả năng anh Văn ném được khoảng bao nhiêu mét là cao nhất?
Lời giải:
a) Cự li trung bình ở mỗi lần ném là:
(mét).
b)
|
Cự li (m) |
[69,2; 70) |
[70; 70,8) |
[70,8; 71,6) |
[71,6; 72,4) |
[72,4; 73,2) |
|
Số lần |
4 |
2 |
7 |
12 |
5 |
c) Ta có:
|
Cự li (m) |
[69,2; 70) |
[70; 70,8) |
[70,8; 71,6) |
[71,6; 72,4) |
[72,4; 73,2) |
|
Giá trị đại diện |
69,6 |
70,4 |
71,2 |
72 |
72,8 |
|
Số lần |
4 |
2 |
7 |
12 |
5 |
Cự li trung bình ước lượng là:
(m).
d) Anh Văn ném được khoảng 73 mét cao nhất.
a) Tính số xe trung bình đi qua trạm thu phí trong mỗi phút.
b) Tổng hợp lại số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng trung bình số xe đi qua trạm thu phí trong mỗi phút từ bảng tần số ghép nhóm trên.
Lời giải:
a) Số xe trung bình đi qua trạm thu phí trong mỗi phút là:
(xe).
b) Ta có bảng sau:
|
Số xe |
[6; 10] |
[11; 15] |
[16; 20] |
[21; 25] |
[26; 30] |
|
Số lần |
5 |
9 |
3 |
9 |
4 |
c) Ta có bảng giá trị đại diện sau:
|
Số xe |
[6; 10] |
[11; 15] |
[16; 20] |
[21; 25] |
[26; 30] |
|
Giá trị đại diện |
8 |
13 |
18 |
23 |
28 |
|
Số lần |
5 |
9 |
3 |
9 |
4 |
Số xe trung bình ước lượng đi qua trạm thu phí từ bảng tần số ghép nhóm trên là:
(xe).
Hãy ướng lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Lời giải:
Ta có bảng giá trị đại diện sau:
|
Số sách |
[16; 20] |
[21; 25] |
[26; 30] |
[31; 35] |
[36; 40] |
[41; 45] |
[46; 50] |
|
Giá trị đại diện |
18 |
23 |
28 |
33 |
38 |
43 |
48 |
|
Số ngày |
3 |
6 |
15 |
27 |
22 |
14 |
5 |
Ước lượng số trung bình của mẫu số liệu trên là:
(quyển).
Mốt của mẫu số liệu trên là:
.
Ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Lời giải:
Ta có bảng giá trị đại diện sau:
|
Chiều cao của cây |
[8,5; 8,8) |
[8,8; 9,1) |
[9,1; 9,4) |
[9,4; 9,7) |
[9,7; 10) |
|
Giá trị đại diện |
8,65 |
8,95 |
9,25 |
9,55 |
9,85 |
|
Số cây |
20 |
35 |
60 |
55 |
30 |
Ước lượng số trung bình của mẫu số liệu là:
(m).
Mốt của mẫu số liệu ghép nhóm trên là:
(m).
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm
Bài 1: Tìm hiểu hàm số lượng giác bằng phần mềm GeoGebra
Lý thuyết Số trung bình và mốt của mẫu số liệu ghép nhóm
1. Số liệu ghép nhóm
- Mẫu số liệu ghép nhóm là thường được trình bày dưới dạng bảng thống kê có dạng như sau:
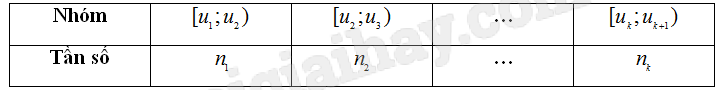
Bảng 1. Bảng tần số ghép nhóm
- Bảng trên gồm k nhóm với , mỗi nhóm gồm một số giá trị được ghép theo một tiêu chí xác định.
- Cỡ mẫu
- Giá trị chính giữ mỗi nhóm được dùng làm giá trị đại diện.
- Hiệu được gọi là độ dài của nhóm
- Sử dụng từ đến nhóm. Cỡ mẫu càng lớn thì cần càng nhiều nhóm số liệu.
- Các nhóm có cùng độ dài bằng L thỏa mãn R<k, trong đó R là khoảng biến thiên, k là số nhóm.
- Giá trị nhỏ nhất của mẫu thuộc vào nhóm và càng gần càng tốt. Giá trị lớn nhất của mẫu thuộc nhóm và càng gần càng tốt.
* Chú ý:
Các đầu mút của nhóm có thể không là giá trị của mẫu số liệu.
2. Số trung bình

Số trung bình của mẫu số liệu ghép nhóm kí hiệu là được tính như sau:
Trong đó, là cỡ mẫu.
Ý nghĩa: Số trung bình của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho số trung bình của mẫu số liệu gốc. Nó thường dùng để đo xu thế trung tâm của mẫu số liệu.
3. Mốt
- Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn.
Giả sử nhóm chứa mốt là: .Khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là được xác định bời công thức:
- Nếu không có nhóm kề trước của nhóm chứa mốt thì . Nếu không có hóm kề sau của nhóm chứa mốt thì .
- Mốt của mẫu số liệu ghép nhóm là giá trị có khả năng xuất hiện cao nhất khi lấy mốt của mẫu số liệu sau khi ghép nhóm xấp xỉ với mốt của mẫu số liệu không ghép nhóm. Các giá trị nằm xung quanh thường có khả năng xuất hiện cao hơ các giá trị khác.
- Một mẫu có thể không có mốt hoặc có nhiều hơn một mốt.