Với giải Bài 2.13 trang 51 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài 6: Cấp số cộng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 6: Cấp số cộng
Bài 2.13 trang 51 Toán 11 Tập 1: Một kiến trúc sư thiết kế một hội trường với 15 ghế ngồi ở hàng thứ nhất, 18 ghế ngồi ở hàng thứ hai, 21 ghế ngồi ở hàng thứ ba, và cứ như vậy (số ghế ở hàng sau nhiều hơn 3 ghế so với số ghế ở hàng liền kề trước nó). Nếu muốn hội trường đó có sức chứa ít nhất 870 ghế ngồi thì kiến trúc sư đó phải thiết kế tối thiểu bao nhiêu hàng ghế?
Lời giải:
Số ghế ở mỗi hàng của hội trường lập thành một cấp số cộng với số hạng đầu u1 = 15 và công sai d = 3. Giả sử cần thiết kế tối thiếu n hàng ghế để hội trường có sức chứa ít nhất 870 ghế ngồi.
Ta có: Sn =
Do đó, n(30 + 3n – 3) ≥ 1 740
⇔ n(3n + 27) – 17 40 ≥ 0
⇔ 3n2 + 27n – 1 740 ≥ 0
Vậy cần thiết kế tối thiểu 20 hàng ghế để thỏa mãn yêu cầu bài toán.
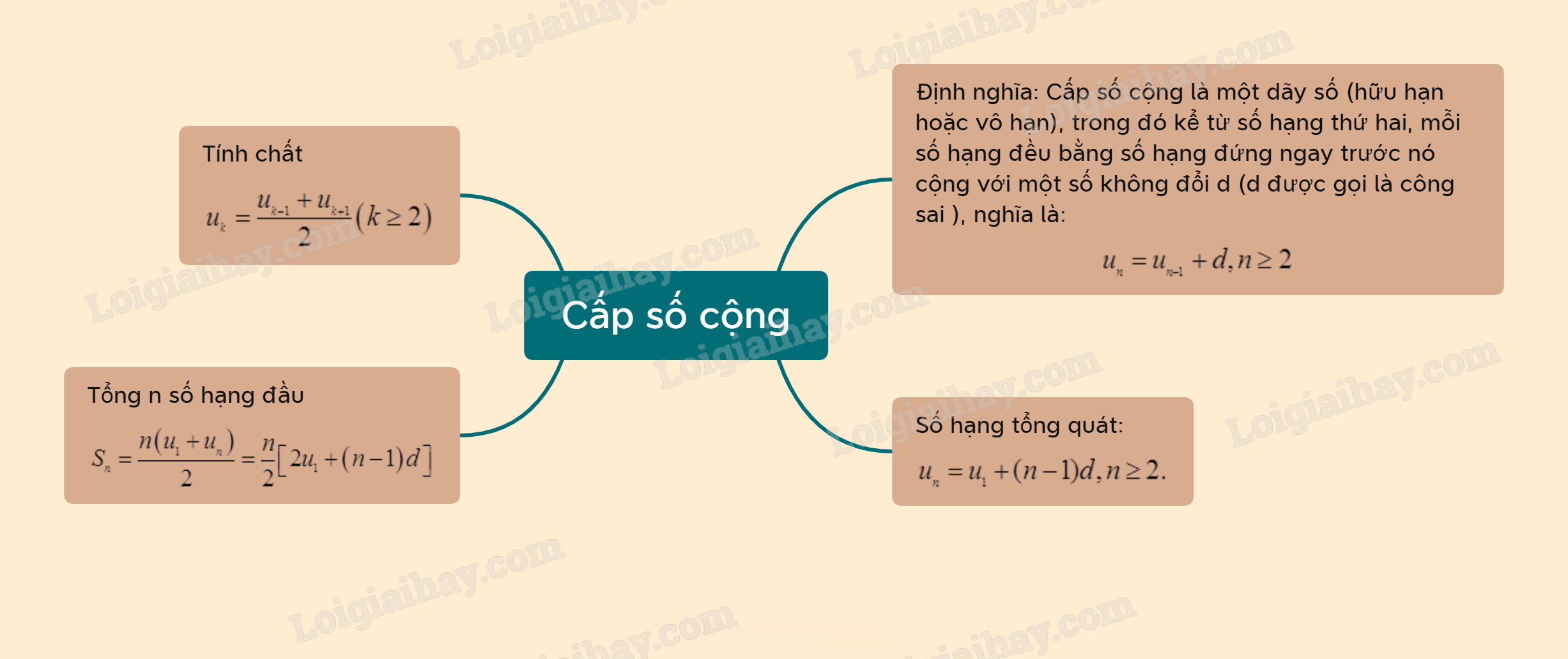
Sơ đồ tư duy Cấp số cộng.
Video bài giảng Toán 11 Bài 6: Cấp số cộng - Kết nối tri thức
Xem thêm các lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Câu hỏi trang 48 Toán 11 Tập 1: Dãy số không đổi a, a, a, ... có phải là một cấp số cộng không?..
HĐ2 trang 49 Toán 11 Tập 1: Cho cấp số cộng (un) với số hạng đầu u1 và công sai d......
HĐ3 trang 50 Toán 11 Tập 1: Cho cấp số cộng (un) với số hạng đầu u1 và công sai d.....
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
