Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 11 Cấp số cộng, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Cấp số cộng. Mời các bạn đón xem:

Bài tập Toán 11 Cấp số cộng

A. Bài tập Cấp số cộng

Bài 1: Xác định công sai, số hạng thứ 5, số hạng tổng quát và số hạng thứ 100 của mỗi cấp số cộng sau:

a) 3, 8, 13, 18, ...;

b) 1, –2, –5, –8, ...

Hướng dẫn giải

a) Ta thấy: 8 – 3 = 5; 13 – 8 = 5

Suy ra cấp số cộng có u₁ = 3, công sai d = 5

Số hạng tổng quát của dãy số là: u_n = 3 + 5(n – 1) = 3 + 5n – 5 = 5n – 2.

Số hạng thứ 5: u₅ = 3 + 5 . (5 – 1) = 23

Số hạng thứ 100: u₁₀₀ = 3 + 5 . (100 – 1) = 498.

b) Ta thấy: –2 – 1= –3; –5 – (–2) = –3

Suy ra cấp số cộng có u₁ = 1, công sai d = –3

Số hạng tổng quát của dãy số là: u_n = 1 – 3(n − 1) = 1 – 3n + 3 = 4 – 3n.

Số hạng thứ 5: u₅ = 1 − 3. (5 – 1) = −11

Số hạng thứ 100: u₁₀₀ = 1 – 3. (100 – 1) = −296.

Bài 2: Viết năm số hạng đầu của mỗi dãy số (u_n) sau và xét xem nó có phải là cấp số cộng không. Nếu dãy số đó là cấp số cộng, hãy tìm công sai d và viết số hạng tổng quát của nó dưới dạng u_n = u₁ + (n – 1)d.

a) u_n = 3 + 4n;

b) u_n = 6n − 4;

c) u₁ = 3, u_n = u_n–1 + n.

Hướng dẫn giải

a) u₁ = 7; u₂ = 11; u₃ = 15; u₄ = 19; u₅ = 23

Ta có: u_n − u_n–1 = 3 + 4n − [3 + 4(n − 1)] = 4, với ∀n ≥ 2.

Suy ra dãy số là cấp số cộng có u₁ = 7 và công sai d = 4

Số hạng tổng quát: u_n = 7 + 4(n − 1).

b) u₁ = 2; u₂ = 8; u₃ = 14; u₄ = 20; u₅ = 26

Ta có: u_n − u_n–1 = 6n − 4 − [6(n − 1) − 4] = 6, với ∀ n ≥ 2.

Suy ra dãy số là cấp số cộng có u₁ = 2 và công sai d = 6.

Số hạng tổng quát: u_n = 2 + 6(n − 1).

c) u₁ = 3; u₂ = 5; u₃ = 8; u₄ = 12; u₅ =17

Ta có: u₂ − u₁ = 2 ≠ u₃ – u₂ = 3

Suy ra đây không phải cấp số cộng.

Bài 3: Một cấp số cộng có số hạng thứ 5 bằng 22 và số hạng thứ 12 bằng 43. Tìm số hạng thứ 50 của cấp số cộng này.

Hướng dẫn giải

Giả sử u₁ là số hạng đầu và d là công sai của cấp số cộng đó. Ta có:

u₅ = u₁ + 4d = 22

u₁₂ = u₁ + 11d = 43

Giải hệ phương trình gồm hai phương trình trên ta được u₁ = 10 và d = 3.

Vậy số hạng thứ 50 của cấp số cộng này là u₅₀ = u_1­ + 49d = 10 + 49 . 3 = 157.

Bài 4: Một cấp số cộng có số hạng đầu bằng 1 và công sai bằng 4. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng 561?

Hướng dẫn giải

Gọi n là số các số hạng đầu cần lấy tổng, ta có:

561 = S_n =$\frac{n}{2}$[2.1+(n-1).4] = $\frac{n}{2}$(-2+4n) = –n + 2n²

Do đó 2n² – n – 561 = 0.

Giải phương trình bậc hai này ta được n = –16,5 (loại) hoặc n = 17.

Vậy ta phải lấy 17 số hạng đầu của cấp số cộng đã cho để có tổng bằng 561.

Bài 5: Vào năm 2020, dân số của một thành phố là khoảng 1,5 triệu người. Giả sử mỗi năm, dân số của thành phố này tăng thêm khoảng 15 nghìn người. Hãy ước tính dân số của thành phố vào năm 2030.

Hướng dẫn giải

Dân số mỗi năm của thành phố lập thành cấp số cộng có u₁ = 1 500 (nghìn người), công sai d = 15.

Dân số mỗi năm có dạng tổng quát là: u_n = 1 500 + 15(n − 1).

Dân số của năm 2030 tức n = 11 thì u₁₁ = 1 500 + 15 . (11 − 1) = 1 650 (nghìn người)

Vậy ước tính dân số của thành phố năm 2030 là 1650 nghìn người hay 1,65 triệu người.

Bài 6. Cho cấp số cộng (u_n) có u₁ = 321 và u_{n + 1} = u_n – 3, ∀n ∈ ℕ*. Số 99 là số hạng thứ bao nhiêu trong dãy số?

A. 72;

B. 73;

C. 74;

D. 75.

Hướng dẫn giải

Đáp án đúng là: D

Ta có: u_{n + 1} = u_n – 3 ⇒ u_{n + 1} − u_n = −3 ⇒ d = −3.

u_n = u₁ + (n – 1)d = 321 + (n – 1)(−3) = −3n + 324.

Ta có: u_n = 99 ⇒ −3n + 324 = 99

⇒ −3n = −225 ⇒ n = 75.

Vậy 99 là số hạng thứ 75 trong dãy số.

Bài 7. Cho cấp số cộng (u_n) có u₂ = 2017 và u₃ = 1945. Số hạng thứ 6 của cấp số cộng đã cho bằng bao nhiêu?

Hướng dẫn giải

Ta có u₃ – u₂ = 1945 – 2017 = –72 ⇒ d = −72.

⇒ u₁ = u₂ − d = 2017 + 72 = 2089.

u₆ = u₁ + 5d = 2089 + 5.(−72) = 1729.

Vậy số hạng thứ 6 của cấp số cộng đã cho là 1729.

Bài 8. Cho cấp số cộng (u_n) có $u_1=\frac{1}{3},u_8=26$ . Tìm d và xác định công thức số hạng tổng quát của cấp số cộng đã cho.

Hướng dẫn giải

Ta có <$u_8=u_1+7d \iff 26=\frac{1}{3}+7d$ 

$\iff 7d=\frac{77}{3}$$\iff d=\frac{11}{3}.$

Vậy công thức số hạng tổng quát của cấp số cộng (u_n) là $u_n=u_1+\frac{11}{3}\left(\mathrm{(n}–\mathrm{1)}\right)$

Bài 9. Cho dãy số (u_n) với u_n = 5 – 3n.

a) Chứng minh dãy số (u_n) là cấp số cộng. Chỉ rõ u₁ và d.

b) Tìm tổng của 100 số hạng đầu tiên của dãy.

Hướng dẫn giải

a) Xét hiệu u_{n + 1} – u_n = [5 – 3(n + 1)] – (5 – 3n) = –3.

Do đó u_{n + 1} = u_n + (–3)

Suy ra dãy số (u_n) là cấp số cộng; u₁ = 5 – 3.1 = 2; công sai d = –3.

b) Tổng của 100 số hạng đầu tiên của dãy là:

.

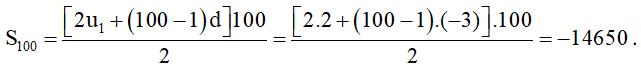
Bài 10. Cho cấp số cộng có u₁ = 3; công sai d = 4.

a) Viết công thức của số hạng tổng quát u_n.

b) Số 155 là số hạng thứ mấy của cấp số cộng trên?

c) Tính tổng 200 số hạng đầu của dãy.

Hướng dẫn giải

a) Ta có công thức của số hạng tổng quát u_n là:

u_n = u₁ + (n – 1).d = 3 + (n – 1).4 = 4n – 1.

Vậy u_n = 4n – 1.

b) Giả sử 155 là số hạng thứ n của cấp số cộng. Ta có:

$n=\frac{u_n-u_1}{d}+1=\frac{155-3}{4}+1=39$.

Vậy 155 là số hạng thứ 39 của cấp số cộng.

c) Tổng 200 số hạng đầu của dãy là:

.

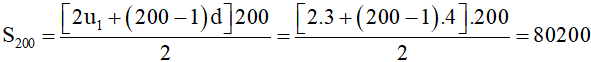
Vậy tổng 200 số hạng đầu của dãy là S₂₀₀ = 80200.

B. Lý thuyết Cấp số cộng

1. Cấp số cộng

- Cấp số cộng là một dãy số (vô hạn hoặc hữu hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó với một số d không đổi, nghĩa là:

u_{n + 1} = u_n + d với n ∈ ℕ*.

Số d được gọi là công sai của cấp số cộng.

Ví dụ: Cho cấp số cộng: $-\frac{1}{2};0;\frac{1}{2};\frac{3}{2};\mathrm{...}$ Tìm số hạng đầu, công sai và u₅.

Hướng dẫn giải

Cấp số cộng đã cho có số hạng đầu $u_1=-\frac{1}{2}$; công sai $d=\frac{1}{2}$.

Ta có $u_4=\frac{3}{2}$ nên $u_5=u_4+d=\frac{3}{2}+\frac{1}{2}=2.$

2. Số hạng tổng quát của cấp số cộng

Định lí 1: Nếu một cấp số cộng (u_n) có số hạng đầu u₁ và công sai d thì số hạng tổng quát u_n của nó được xác định bởi công thức:

u_n = u₁ + (n – 1)d, n ≥ 2.

Ví dụ: Cho một cấp số cộng có u₁ = −3; u₆ = 27.

Hướng dẫn giải

Ta có: u₆ = u₁ + (6 – 1)d = 27

⇔ −3 + 5d = 27 ⇔ 5d = 30 ⇔ d = 6.

3. Tổng của n số hạng đầu tiên của cấp số cộng

Định lí 2: Giả sử (u_n) là một cấp số cộng có công sai d. Đặt S_n = u₁ + u₂ + ... + u_n, khi đó

Ví dụ: Cho cấp số cộng (u_n) có u₁ = −3; d = 2.

Vậy tổng của 5 số hạng đầu tiên của dãy số (u_n) là 5.

Video bài giảng Toán 11 Bài 6: Cấp số cộng - Kết nối tri thức