Bài 5.4 trang 109 Toán 11 Tập 1 Kết nối tri thức | Giải bài tập Toán lớp 11

Bài 5.4 trang 109 Toán 11 Tập 1 Kết nối tri thức | Giải bài tập Toán lớp 11

Van Anh Ngày: 11-08-2024 Lớp 11

670

Với giải Bài 5.4 trang 109 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài 15: Giới hạn của dãy số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 15: Giới hạn của dãy số

Bài 5.4 trang 109 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số:

a) 1,(12) = 1,121212...;

b) 3,(102) = 3,102102102...

Lời giải:

a) Ta có: 1,(12) = 1,121212... = 1 + 0,12 + 0,0012 + 0,000012 + ...

= 1 + 12 . 10^-2 + 12 . 10^-4 + 12 . 10^-6 + ...

= 1 + 12 . (10^-2 + 10^-4 + 10^-6 + ...)

Do 10^-2 + 10^-4 + 10^-6 + ... là tổng của cấp số nhân lùi vô hạn với u₁ = 10^-2 và q = 10^-2 nên

10^-2 + 10^-4 + 10^-6 + ... = $\frac{10^{- 2}}{1 - 10^{- 2}} = \frac{1}{99}$ .

Vậy 1,(12) = $1 + 12. \frac{1}{99} = \frac{33}{33} + \frac{4}{33} = \frac{37}{33}$ .

b) Ta có: 3,(102) = 3,102102102... = 3 + 0,102 + 0,000102 + 0,000000102 + ...

= 3 + 102 . 10^-3 + 102 . 10^-6 + 102 . 10^-9 + ...

= 3 + 102 . (10^-3 + 10^-6 + 10^-9 + ...)

Do 10^-3 + 10^-6 + 10^-9 + ... là tổng của cấp số nhân lùi vô hạn với u₁ = 10^-3 và q = 10^-3 nên

10^-3 + 10^-6 + 10^-9 + ... = $\frac{10^{- 3}}{1 - 10^{- 3}} = \frac{1}{999}$ .

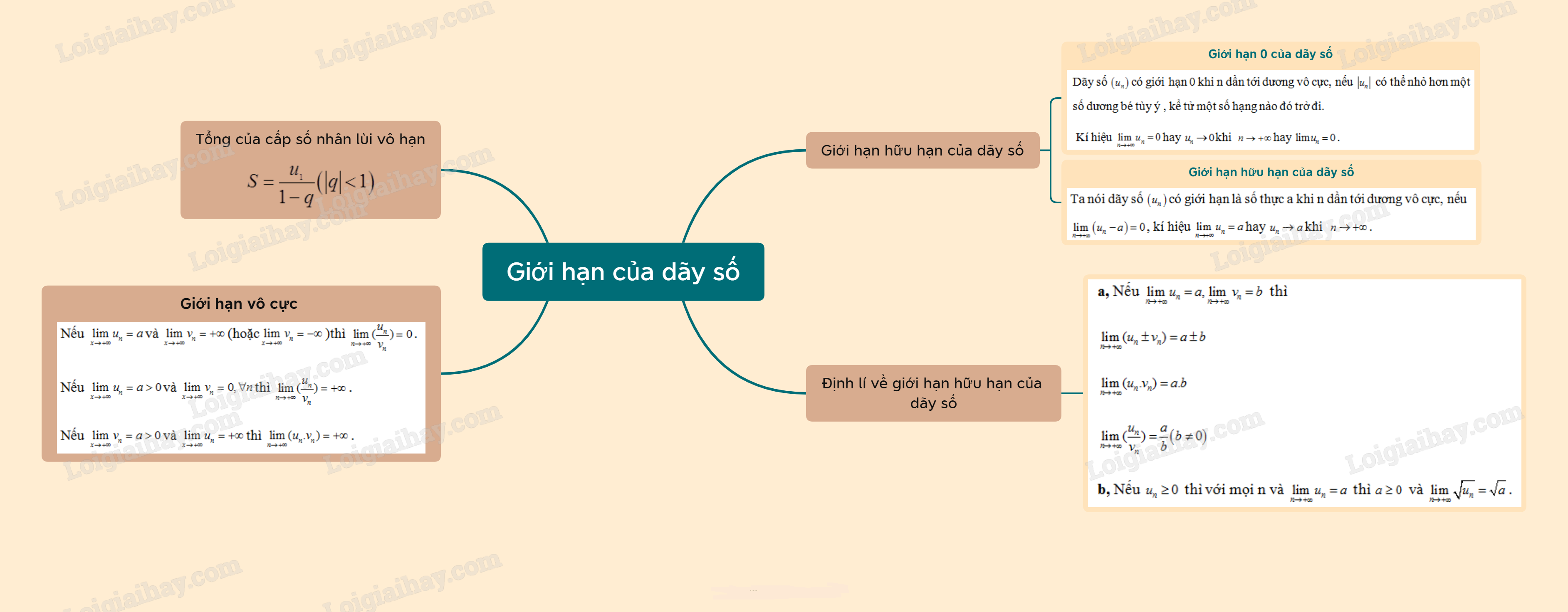
Vậy 3,(102) = 3 + $102. \frac{1}{999} = 3 + \frac{34}{333} = \frac{1033}{333}$ .

Sơ đồ tư duy Giới hạn của dãy số.

Video bài giảng Toán 11 Bài 15: Giới hạn của dãy số - Kết nối tri thức

Xem thêm các lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

HĐ1 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn là 0...

Luyện tập 1 trang 105 Toán 11 Tập 1: Chứng minh rằng $\lim_{n \to + \infty} \frac{{(- 1)}^{n - 1}}{3^{n}} = 0$ .....

HĐ2 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn hữu hạn....

Luyện tập 2 trang 106 Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{{3.2}^{n} - 1}{2^{n}}$ . Chứng minh rằng $\lim_{n \to + \infty} u_{n} = 3$ ....

Vận dụng 1 trang 106 Toán 11 Tập 1: Một quả bóng cao su được thả từ độ cao 5 m xuống mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng $\frac{2}{3}$ độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử u_n là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ n. Chứng minh rằng dãy số (u_n) có giới hạn là 0.....

HĐ3 trang 106 Toán 11 Tập 1: Hình thành quy tắc tính giới hạn....

Luyện tập 3 trang 107 Toán 11 Tập 1: Tìm $\lim_{n \to + \infty} \frac{\sqrt{2 n^{2} + 1}}{n + 1}$ .....

HĐ4 trang 107 Toán 11 Tập 1: Làm quen với việc tính tổng vô hạn...

Luyện tập 4 trang 108 Toán 11 Tập 1: Tính tổng $S = 2 + \frac{2}{7} + \frac{2}{49} + ... + \frac{2}{7^{n - 1}} + ...$ ....

Vận dụng 2 trang 108 Toán 11 Tập 1: (Giải thích nghịch lí Zeno)....

HĐ5 trang 108 Toán 11 Tập 1: Nhận biết giới hạn vô cực...

Luyện tập 5 trang 109 Toán 11 Tập 1: Tính $\lim_{n \to + \infty} (n - \sqrt{n})$ .....

Bài 5.1 trang 109 Toán 11 Tập 1: Tìm các giới hạn sau:....

Bài 5.2 trang 109 Toán 11 Tập 1: Cho hai dãy số không âm (u_n) và (v_n) với $\lim_{n \to + \infty} u_{n} = 2$ và $\lim_{n \to + \infty} v_{n} = 3$ . Tìm các giới hạn sau:....

Bài 5.3 trang 109 Toán 11 Tập 1: Tìm giới hạn của các dãy số cho bởi:....

Bài 5.4 trang 109 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số:...

Bài 5.5 trang 109 Toán 11 Tập 1: Một bệnh nhân hằng ngày phải uống một viên thuốc 150 mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể bệnh nhân nếu bệnh nhân sử dụng thuốc trong một thời gian dài.....

Bài 5.6 trang 109 Toán 11 Tập 1: Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA₁ ⊥ BC, từ A₁ kẻ A₁A₂ ⊥ AC, sau đó lại kẻ A₂A₃ ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA₁A₂A₃... Tính độ dài đường gấp khúc này theo h và α.....

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối Chương 5

Từ khóa :

Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

137

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.