Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 11 Giới hạn của dãy số, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Góc lượng giác. Giá trị lượng giác của góc lượng giác. Mời các bạn đón xem:
Bài tập Toán 11 Giới hạn của dãy số
A. Bài tập Giới hạn của dãy số
Bài 1: Tìm các giới hạn sau:
a) (2n3-3n+2);
b) ;
c)
Hướng dẫn giải
a)(2n3-3n+2) = 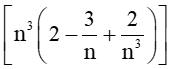
Vì và 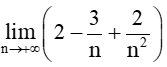
b) = 2.
c)
Bài 2: Cho hai dãy số không âm (un) và (vn) với và . Tìm giới hạn của: .
Hướng dẫn giải
Ta có: , do đó (vn . un) = 5.5 = 25.
(vn - un) = 5-3 = 2.
Vậy = .
Bài 3: Tính tổng của cấp số nhân lùi vô hạn: 3; – 1;
Hướng dẫn giải
un là cấp số nhân lùi vô hạn có số hạng đầu u1 = 3 và công bội q = .
Tổng của cấp số nhân này là: S = = .
Bài 4: Một cấp số nhân lùi vô hạn có tổng các số hạng bằng 56, tổng bình phương các số hạng bằng 448. Số hạng đầu tiên của cấp số nhân đó là bao nhiêu?
Hướng dẫn giải
⇒
Suy ra: q = .
Ta tìm được: u1 = 14.
Bài 5. Tính các giới hạn sau:
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải
a) Ta có 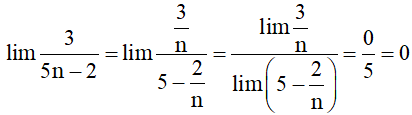
Vậy .
b) Ta có 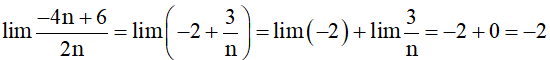
Vậy .
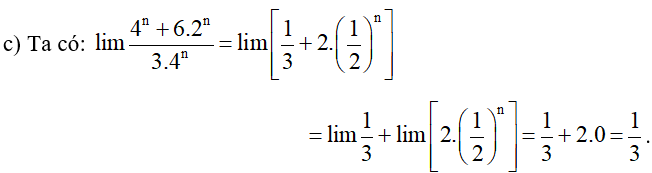
Vậy .
d) Ta có:
Vậy .
Bài 6. Cho và . Tính các giới hạn:
lim (un + vn); lim(un – vn); lim(un.vn); .
Hướng dẫn giải
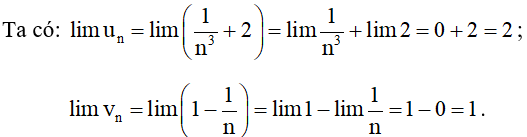
Khi đó:
• lim (un + vn) = lim un + lim vn = 2 + 1 = 3.
• lim (un – vn) = lim un – lim vn = 2 – 1 = 1.
• lim (un . vn) = lim un . lim vn = 2 . 1 = 2
• .
Bài 7. Tính tổng của cấp số nhân lùi vô hạn biết u1 = 1, công bội .
Hướng dẫn giải
Tổng của cấp số nhân lùi vô hạn với u1 = 1, công bội là:
.
Vậy S = 3.
Bài 8. Tính các giới hạn sau:
a) ;
b) ;
c) .
Hướng dẫn giải
a) ;
b) ;
Bài 9. Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có công bội là và tính tổng của cấp số nhân lùi vô hạn.
Hướng dẫn giải
Suy ra số hạng đầu tiên của dãy là: u1 = 1.
Khi đó tổng cấp số nhân lùi vô hạn là:
Vậy số hạng tổng quát của cấp số nhân lùi vô hạn là: 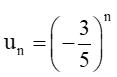
Bài 10. Tính các giới hạn sau:
a) ;
b) .
Hướng dẫn giải
B. Lý thuyết Giới hạn của dãy số
1. Giới hạn hữu hạn của dãy số
1.1. Giới hạn 0 của dãy số
Ta nói (un) có giới hạn 0 khi n dần tới dương vô cực, nếu |un| nhỏ hơn một số dương bé tùy ý cho trước, kể từ một số hạng nào đó trở đi.
Kí hiệu: hay khi
Ví dụ: Cho dãy số (un) với . Tìm giới hạn của dãy số.
Hướng dẫn giải
Với n > 10 000 thì .
Suy ra .
Một vài giới hạn đặc biệt:
• , với k nguyên dương bất kì.
• , với q là số thực thỏa mãn |q| < 1.
Ví dụ: Tìm các giới hạn sau:
a) ;
Hướng dẫn giải
a) Do 3 là một số nguyên dương nên ;
b) Do | nên
1.2. Giới hạn hữu hạn của dãy số
Ta nói dãy số có giới hạn hữu hạn là số a (hay un dần tới a) khi n dần tới dương vô cực, nếu lim (un – a) = 0.
Kí hiệu: hay lim un = a khi n → +∞.
Chú ý: Nếu un = c (c là hằng số) thì
Ví dụ: Cho Chứng minh rằng .
Hướng dẫn giải
Theo định nghĩa, ta có .
2. Các phép toán về giới hạn hữu hạn của dãy số
Cho lim un = a, lim vn = b và c là hằng số. Khi đó:
• lim (un + vn) = a + b
• lim (un – vn) = a – b
• lim (c.un) = c . a
• lim (un.un) = a . b
• )
• Nếu thì và
Ví dụ: Tìm các giới hạn sau:
a)
b) .
Hướng dẫn giải
a) Ta có:
Từ đó:
b)
.
3. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân vô hạn (un) có công bội q thõa mãn |q| < 1 được gọi là cấp số nhân lùi vô hạn.
Cấp số nhân lùi vô hạn nàu có tổng là:
.
Ví dụ: Tính tổng của cấp số nhân lùi vô hạn:
Hướng dẫn giải
Ta có dãy số 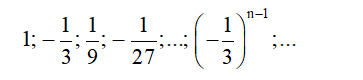
4. Giới hạn vô cực
• Ta nói dãy số (un) có giới hạn là +∞ khi n → +∞, nếu un có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim un = + ∞ hay un → +∞ khi n → +∞.
• Dãy số (un) có giới hạn là −∞ khi n → +∞, nếu lim un = + ∞.
Kí hiệu: lim un = − ∞ hay un → −∞ khi n → +∞.
Chú ý:
• lim un = + ∞ ⇔ lim (−un) = − ∞;
• Nếu lim un = + ∞ hoặc lim un = − ∞ thì ;
• Nếu lim un = 0 và un > 0 với mọi n thì .
Ví dụ: Tìm giới hạn .
Hướng dẫn giải
Từ 2 > 1 suy ra
Mà 2n > 0 với mọi n nên lim 2n = + ∞.
Nhận xét:
• ;
• .
Video bài giảng Toán 11 Bài 15: Giới hạn của dãy số - Kết nối tri thức