Tailieumoi.vn xin giới thiệu đến các quý Thầy/Cô Giáo án Toán lớp 8 Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến sách Cánh diều theo mẫu Giáo án chuẩn của Bộ GD&ĐT. Hi vọng tài liệu này sẽ giúp Giáo viên dễ dàng biên soạn giáo án Toán 8. Chúng tôi rất mong sẽ được thầy/cô đón nhận và đóng góp những ý kiến quý báu của mình.
Chỉ từ 500k mua trọn bộ Giáo án Toán 8 Cánh diều bản word trình bày đẹp mắt, thiết kế hiện đại (chỉ từ 30k cho 1 bài Giáo án lẻ bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official
Xem thử tài liệu tại đây: Link tài liệu
Ngày soạn: …/…/…
Ngày dạy: …/…/…
Bài 1. Đơn thức nhiều biến. Đa thức nhiều biến
I. MỤC TIÊU
1. Kiến thức: Học xong bài này, HS đạt các yêu cầu sau:
– Nhận biết được đơn thức nhiều biến, đơn thức thu gọn, đơn thức đồng dạng, hệ số, phần biến của đơn thức.
– Nhận biết được đa thức.
– Thực hiện thu gọn được đơn thức; cộng và trừ đơn thức đồng dạng; thu gọn được đa thức.
– Tính giá trị của đa thức khi biết giá trị của các biến.
2. Năng lực
Năng lực chung:
– Năng lực tự chủ và tự học trong tìm tòi khám phá.
– Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm.
– Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
– Năng lực tư duy và lập luận toán học: được hình thành thông qua các thao tác như nhận biết đơn thức nhiều biến, đa thức nhiều biến; xác định hệ số, phần biến của đơn thức; thu gọn đơn/ đa thức; ...
– Năng lực giao tiếp toán học: được hình thành qua việc HS sử dụng được các thuật ngữ toán học xuất hiện ở bài học trong trình bày, diễn đạt giải toán như đơn thức nhiều biến, đa thức nhiều biến, đơn thức thu gọn, đơn thức đồng dạng, ...
– Năng lực mô hình hóa toán học: được hình thành thông qua thao tác HS viết được đơn thức biểu thị các đại lượng để mô tả tình huống xuất hiện trong một số bài toán thực tế đơn giản.
– Năng lực giải quyết vấn đề toán học: được hình thành qua việc HS phát hiện được vấn đề cần giải quyết và sử dụng được kiến thức, kĩ năng toán học trong bài học để giải quyết vấn đề.
3. Phẩm chất
– Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm.
– Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.
– Hình thành tư duy logic, lập luận chặt chẽ, và linh hoạt trong quá trình suy nghĩ.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án powerpoint, đồ dùng dạy học, thước thẳng có chia khoảng.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)
a) Mục tiêu:
‒ Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học. Thông qua bài toán mở đầu, HS bước đầu nhận thấy sự cần thiết của đa thức nhiều biến.
b) Nội dung: HS đọc bài toán mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu, bước đầu hình dung vấn đề về đa thức nhiều biến.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
– GV yêu cầu HS đọc bài toán mở đầu được trình chiếu trên màn hình:
Bài toán: “Trong giờ học Mĩ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là \(x\) (cm) và \(y\) (cm) như Hình 1. Viết biểu thức biểu thị tổng diện tích của hình tạo bởi hình tam giác vuông và hai hình vuông đó.”
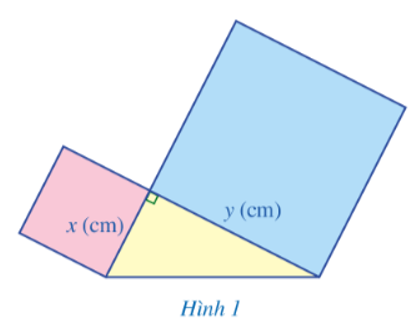
– GV đưa ra câu hỏi gợi mở: “Muốn tính tổng diện tích của hình tạo bởi hình tam giác vuông và hai hình vuông đó, ta phải tính như thế nào?” (GV có thể gợi ý/ yêu cầu HS nhắc lại công thức tính diện tích tam giác vuông và hình vuông).
Bước 2: Thực hiện nhiệm vụ:
– Các nhóm tiến hành thảo luận và thống nhất phương án trả lời câu hỏi của nhóm mình.
– GV quan sát, theo dõi các nhóm thực hiện nhiệm vụ. Giải thích câu hỏi nếu các học sinh không hiểu nội dung các câu hỏi.
Bước 3: Báo cáo, thảo luận:
– Mỗi nhóm cử đại diện trình bày phương án đã thống nhất.
– Các HS còn lại quan sát phương án trả lời của các bạn.
– GV gọi HS nhận xét, bổ sung và chữa bài.
® Dự kiến câu trả lời: Biểu thức biểu thị tổng diện tích của hình tạo bởi hình tam giác vuông và hai hình vuông đó là \({x^2} + {y^2} + \frac{1}{2}xy\).
Bước 4: Kết luận, nhận định:
– GV nhận xét thái độ làm việc, phương án trả lời của các nhóm, ghi nhận và tuyên dương nhóm có câu trả lời tốt nhất. Động viên các nhóm còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo.
– Trên cơ sở đó, GV dẫn dắt vào bài học mới: “Biểu thức đại số \({x^2} + {y^2} + \frac{1}{2}xy\) tìm được ở trên được gọi là gì? Trong bài học này chúng ta sẽ cùng tìm hiểu: Bài 1. Đơn thức nhiều biến. Đa thức nhiều biến”.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Đơn thức nhiều biến
a) Mục tiêu:
‒ HS nhận biết được đơn thức nhiều biến, đơn thức thu gọn, đơn thức đồng dạng;
– HS luyện kĩ năng xác định được hệ số, phần biến của một đơn thức;
– HS hình thành và rèn luyện kĩ năng thu gọn đơn thức và cộng, trừ đơn thức đồng dạng.
b) Nội dung:
– HS tìm hiểu nội dung kiến thức khái niệm đơn thức nhiều biến, đơn thức thu gọn, đơn thức đồng dạng, thực hiện được cộng trừ đơn thức đồng dạng theo yêu cầu, dẫn dắt của GV và thực hiện HĐ1, HĐ2, HĐ3, HĐ4, các Ví dụ, thực hành làm Luyện tập 1, 2, 3, 4 để nắm vững kiến thức.
c) Sản phẩm: HS hình thành được kiến thức, nhận biết được đơn thức nhiều biến và thu gọn chúng; nhận biết được đơn thức đồng dạng và thực hiện cộng, trừ các đơn thức đồng dạng.
d) Tổ chức thực hiện:
|
HOẠT ĐỘNG CỦA GV VÀ HS |
SẢN PHẨM DỰ KIẾN |
||||||||||||||||
|
Bước 1. Chuyển giao nhiệm vụ: Nhiệm vụ 1. Tìm hiểu khái niệm đơn thức nhiều biến – GV yêu cầu HS thảo luận nhóm đôi, thực hiện HĐ1: + GV mời 3 HS trả lời HĐ1, cả lớp nhận xét, GV đánh giá. + GV giới thiệu các biểu thức ở HĐ1 là những đơn thức.
– GV chuẩn hóa kiến thức đưa ra khái niệm đơn thức nhiều biến: “Đơn thức nhiều biến (hay đơn thức) là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.” + HS đọc phần kiến thức trọng tâm. + GV mời 1 số HS lấy ví dụ về đơn thức. – GV yêu cầu HS đọc Ví dụ 1, hoạt động cá nhân sau đó trao đổi hỏi đáp. + GV mời 1 HS giải thích tại sao biểu thức \(2x + y\) không phải là đơn thức. + Các HS khác nhận xét và bổ sung. GV đánh giá và chốt đáp án. – GV yêu cầu HS nhận biết đơn thức bằng cách hoàn thành cá nhân Luyện tập 1. GV mời 1 – 2 HS trả lời, cả lớp nhận xét. GV chốt đáp án.
Nhiệm vụ 2. Tìm hiểu khái niệm đơn thức thu gọn – GV yêu cầu HS thực hiện HĐ2: ® GV giới thiệu đơn thức \[2{x^3}{y^4}\] là đơn thức thu gọn; 2 gọi là hệ số và \[{x^3}{y^4}\] gọi là phần biến của đơn thức đó. – GV chuẩn hóa kiến thức đưa ra khái niệm đơn thức thu gọn: “Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến, mà mỗi biến đã được nâng lên lũy thừa với số mũ nguyên dương và chỉ được viết một lần. Số nói trên gọi là hệ số, phần còn lại gọi là phần biến của đơn thức thu gọn.” + HS đọc phần kiến thức trọng tâm. + GV lưu ý cách viết thông thường: ta viết hệ số trước, phần biến sau, các biến được viết theo thứ tự bảng chữ cái. – GV yêu cầu HS đọc Ví dụ 2, thảo luận trao đổi cặp đôi. – GV yêu cầu HS thực hành thu gọn đơn thức thông qua việc hoàn thành Luyện tập 2. GV mời 1 HS lên bảng trình bày, các HS khác quan sát và nhận xét; GV đánh giá mức độ hiểu bài của HS và chốt đáp án. – GV lưu ý cho HS phần Chú ý: + Ta cũng coi một số là đơn thức thu gọn. + Từ nay, khi nói đến đơn thức, nếu không nói gì thêm, ta hiểu đó là đơn thức thu gọn. Nhiệm vụ 3. Tìm hiểu đớn thức đồng dạng – GV yêu cầu HS tự thực hiện cá nhân HĐ3. GV mời 1 – 2 HS trình bày miệng, các HS khác lắng nghe và nhận xét. ® GV giới thiệu hai đơn thức \(2{x^3}{y^4}\) và \( - 3{x^3}{y^4}\) có hệ số khác 0 và có cùng phần biến là hai đơn thức đồng dạng. – GV chuẩn hóa kiến thức, đưa ra khái niệm hai đơn thức đồng dạng: “Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.” + HS đọc kiến thức trọng tâm. + GV nhấn mạnh cho HS về hệ số của đơn thức phải khác 0. + GV mời 1 – 2 HS lấy ví dụ về hai đơn thức đồng dạng. – GV hướng dẫn mẫu cho HS làm Ví dụ 3. – GV yêu cầu HS tự thực hiện Luyện tập 3, giải thích vì sao các đơn thức trong từng trường hợp đồng dạng hay không đồng dạng.
Nhiệm vụ 4. Tìm hiểu quy tắc cộng, trừ các đơn thức đồng dạng – GV yêu cầu HS thảo luận nhóm đôi, thực hiện HĐ4. + GV có thể mời 1 HS nhắc lại quy tắc cộng, trừ các đơn thức một biến có cùng số mũ. + GV hướng dẫn, dẫn dắt HS quy tắc cộng, trừ các đơn thức đồng dạng: Tương tự như đơn thức một biến có cùng số mũ của biến, đối với đơn thức nhiều biến đồng dạng ta cũng có quy tắc sau: “Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.” + GV lưu ý cho HS chỉ thực hiện cộng, trừ với các đơn thức đồng dạng với nhau. – GV yêu cầu HS đọc Ví dụ 4, trao đổi hỏi đáp. – GV tổ chức cho HS hoạt động cặp đôi hoàn thành Luyện tập 4, GV mời 2 HS lên bảng trình bày, các HS khác tự hoàn thành vào vở và nhận xét bài bạn. GV đánh giá và chốt đáp án.
Bước 2. Thực hiện nhiệm vụ: – HS theo dõi SGK, chú ý nghe, tiếp nhận kiến thức, hoàn thành các yêu cầu, hoạt động cặp đôi, kiểm tra chéo đáp án theo sự điều hành của GV. – GV dẫn dắt, phân tích, điều hành và quan sát, trợ giúp HS. |
I. Đơn thức nhiều biến 1. Khái niệm HĐ1: a) Biểu thức biểu thị: – Diện tích của hình vuông có độ dài cạnh là \(x\) (cm) là \[{x^2}\] (cm2). – Diện tích của hình chữ nhật có độ dài hai cạnh lần lượt là \[2x\] (cm), \[3y\] (cm) là: \[2x.3y\] (cm2). – Thể tích của hình hộp chữ nhật có ba kích thước lần lượt là \(x\) (cm), \(2y\) (cm), \(3z\) (cm) là: \(x.2y.3z\) (cm3). b)
Þ Kết luận: Khái niệm đơn thức nhiều biến: “Đơn thức nhiều biến (hay đơn thức) là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.”
Ví dụ 1: SGK – tr6.
Luyện tập 1: Các biểu thức là đơn thức gồm: \[3{x^3}y\]; \(5y;\,\,\frac{1}{2}{x^3}{y^2}{x^2}z\).
2. Đơn thức thu gọn HĐ2: Trong đơn thức \[2{x^3}{y^4}\], mỗi biến \(x\) và \(y\) được viết một lần dưới dạng một lũy thừa với số mũ nguyên dương.
Þ Kết luận: Khái niệm đơn thức thu gọn: “Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến, mà mỗi biến đã được nâng lên lũy thừa với số mũ nguyên dương và chỉ được viết một lần. Số nói trên gọi là hệ số, phần còn lại gọi là phần biến của đơn thức thu gọn.”
Ví dụ 2: SGK – tr6.
Luyện tập 2: • \[{y^3}{y^2}z = {y^5}z\]; • \(\frac{1}{3}x{y^2}{x^3}z = \frac{1}{3}\left( {x\,.\,{x^3}} \right){y^2}z = \frac{1}{3}{x^5}{y^2}z\).
3. Đơn thức đồng dạng HĐ3: a) Hệ số của \(2{x^3}{y^4}\) là 2; Hệ số của \( - 3{x^3}{y^4}\) là \( - 3\). b) Phần biến của hai đơn thức đều giống nhau là \[{x^3}{y^4}\].
Þ Kết luận: “Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.”
Ví dụ 3: SGK – tr7. Luyện tập 3: a) Các đơn thức \[{x^2}{y^4}; - 3{x^2}{y^4}\] và \(\sqrt 5 {x^2}{y^4}\) đồng dạng vì chúng có hệ số khác 0 và có cùng phần biến là \[{x^2}{y^4}\]. b) Hai đơn thức \( - {x^2}{y^2}{z^2}\) và \( - 2{x^2}{y^2}{z^3}\) không đồng dạng vì chúng không có cùng phần biến. 4. Cộng, trừ các đơn thức đồng dạng
HĐ4: a) \[5{x^3} + 8{x^3} = \left( {5 + 8} \right){x^3} = 13{x^3}\]; b) \[10{y^7} - 15{y^7} = \left( {10 - 15} \right){y^7} = - 5{y^7}\].
=> Kết luận: Quy tắc cộng, trừ các đơn thức đồng dạng:
|
................................................
................................................
................................................
Tài liệu có 19 trang, trên đây trình bày tóm tắt 5 trang của Giáo án Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến
Để mua Giáo án Toán lớp 8 Cánh diều năm 2024 mới nhất, mời Thầy/Cô liên hệ Mua tài liệu có đáp án, Ấn vào đây
Xem thêm các bài Giáo án Toán lớp 8 Cánh diều hay, chi tiết khác:
Giáo án Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến
Giáo án Bài 2: Các phép tính với đa thức nhiều biến
Giáo án Bài 3: Hằng đẳng thức đáng nhớ
Giáo án Bài 4: Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
