Với giải HĐ Khám phá 2 trang 89 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 2: Tổng và hiệu của hai vecto học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 2: Tổng và hiệu của hai vecto
HĐ Khám phá 2 trang 89 Toán lớp 10: Cho hình bình hành ABCD (Hình 4). Chứng minh rằng:
Phương pháp giải:
Tìm vectơ bằng với vectơ , sau đó áp dụng quy tắc ba điểm
Lời giải:
Vì ABCD là hình bình hành nên ta có: (đpcm)
Lý thuyết Tổng của hai vectơ
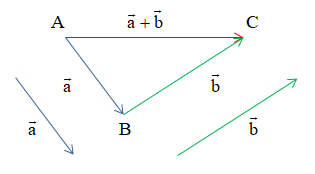
Cho hai vectơ và . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho . Khi đó được gọi là tổng của hai vectơ và và được kí hiệu là .
Vậy .
Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.
Quy tắc ba điểm
Với ba điểm M, N, P, ta có .
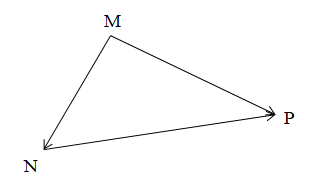Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.
Ví dụ: Cho các điểm A, B, C, D, E, F phân biệt. Thực hiện phép cộng các vectơ:
.
Hướng dẫn giải
Áp dụng quy tắc ba điểm, ta có:
.
.
.
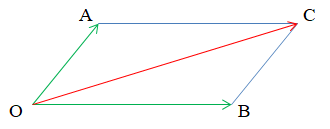
Quy tắc hình bình hành
Nếu OACB là hình bình hành thì ta có .
Ví dụ: Cho hình chữ nhật MNPQ và hai vectơ như hình bên. Tính tổng của hai vectơ và .
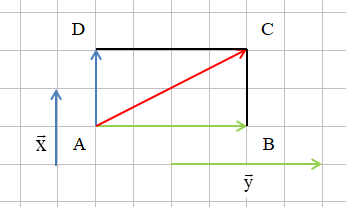
Hướng dẫn giải
Ta có .
Suy ra .
Theo quy tắc hình bình hành, ta có .
Vậy .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
