Với Giải toán 10 trang 68 Tập 2 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải toán 10 trang 68 Tập 2 Chân trời sáng tạo

Khám phá 5 trang 68 Toán lớp 10: Trong mặt phẳng Oxy, cho điểm $F\left(0;\frac{1}{2}\right)$, đường thẳng $\mathrm{\Delta }:y+\frac{1}{2}=0$ và điểm $M(x;y)$. Để tìm hệ thức giữa x và y sao cho $M$ cách đều  F và $\mathrm{\Delta }$, một học sinh đã làm như sau:

+) Tính MF và MH (với H là hình chiếu của M trên $\mathrm{\Delta }$):

$MF=\sqrt{x^2+{\left(y-\frac{1}{2}\right)}^2},MH=d\left(M,\mathrm{\Delta }\right)=\left|y+\frac{1}{2}\right|$

+) Điều kiện để M cách đều F  và $\mathrm{\Delta }$:

$\begin{array}{l}MF=d\left(M,\mathrm{\Delta }\right)\iff \sqrt{x^2+{\left(y-\frac{1}{2}\right)}^2}=\left|y+\frac{1}{2}\right|\\ \iff x^2+{\left(y-\frac{1}{2}\right)}^2={\left(y+\frac{1}{2}\right)}^2\\ \iff x^2=2y\iff y=\frac{1}{2}{x}^2(\ast )\end{array}$

Hãy cho biết tên đồ thị (P) của hàm số (*) vừa tìm được.

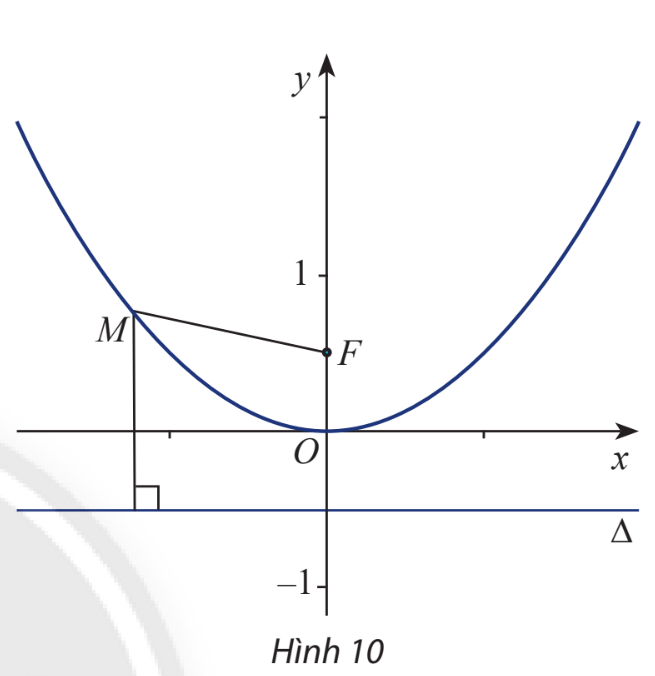
Lời giải:

Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.

Khám phá 6 trang 68 Toán lớp 10: Cho parabol (P) có tiêu điểm F  và đường chuẩn $\mathrm{\Delta }$. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên $p>0$

Chọn hệ trục tọa độ Oxy sao cho $F\left(\frac{p}{2};0\right)$ và $\mathrm{\Delta }:x+\frac{p}{2}=0$

Xét điểm $M(x;y)$

a) Tính MF và $d\left(M,\mathrm{\Delta }\right)$

b) Giải thích biểu thức sau:

$M(x;y)\in (P)\iff \sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=\left|x+\frac{p}{2}\right|$

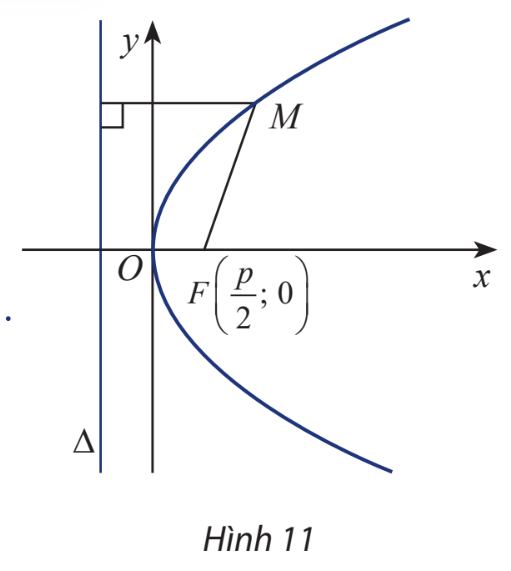
Phương pháp giải:

Sử dụng phương pháp tọa độ trong mặt phẳng

Lời giải:

a) Ta có: $\overrightarrow{FM}=\left(x-\frac{p}{2};y\right)\Rightarrow MF=\left|\overrightarrow{FM}\right|=\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}$

$d\left(M,\mathrm{\Delta }\right)=\frac{\left|x+\frac{p}{2}\right|}{1}=\left|x+\frac{p}{2}\right|$

b) M thuộc parabol (P) nên M cách đều F và $\mathrm{\Delta }$

Suy ra $MF=d\left(M,\mathrm{\Delta }\right)\iff \sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=\left|x-\frac{p}{2}\right|$

Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Giải toán lớp 10 trang 63 Tập 2

Giải toán lớp 10 trang 64 Tập 2

Giải toán lớp 10 trang 65 Tập 2

Giải toán lớp 10 trang 66 Tập 2

Giải toán lớp 10 trang 67 Tập 2

Giải toán lớp 10 trang 70 Tập 2

Giải toán lớp 10 trang 71 Tập 2

Giải toán lớp 10 trang 73 Tập 2