Với giải Vận dụng 2 trang 53 SGK Toán 10 Kết nối tri thức chi tiết trong Bài 22: Ba đường Conic giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 22: Ba đường Conic
Vận dụng 2 trang 53 Toán 10 Tập 2: Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gì? Vì sao?
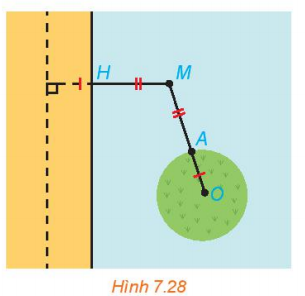
Lời giải:
Gọi d là đường bờ biển, kẻ một đường thẳng ∆ nằm trong đất liền song song với d sao cho khoảng cách giữa hai đường thẳng OA.
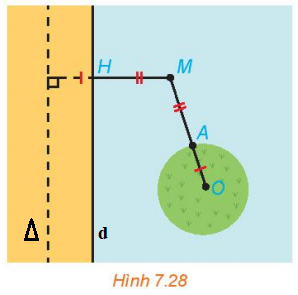
Khi đó ta có:
d(M; ∆) = MH + OA
Mà MH = MA nên d(M; ∆) = MH + OA = MA + OA = MO
Ta có khoảng cách từ điểm M bất kì thuộc đường ranh giới đến đường thẳng ∆ bằng với khoảng cách từ điểm M đến điểm O là tâm của hòn đảo.
Nếu ta coi ∆ là đường chuẩn, điểm O của hòn đảo là vị trí tiêu điểm F thì điểm M cách đều đường chuẩn ∆ và tiêu điểm F nên M nằm trên đường parabol.
Vậy đường ranh giới là tập hợp các điểm cách đều đất liền và đảo hay chính là đường parabol.
Xem thêm lời giải sách giáo khoa Toán 10 Kết nối tri thức hay, chi tiết khác:
Câu hỏi trang 49 Toán 10 Tập 2: Tại sao trong định nghĩa elip cần điều kiện a > c?...
Câu hỏi trang 50 Toán 10 Tập 2: Tại sao trong định nghĩa hypebol cần điều kiện a < c?...
Luyện tập 4 trang 52 Toán 10 Tập 2: Cho (H) : . Tìm các tiêu điểm và tiêu cự của (H)...
Bài 7.19 trang 56 Toán 10 Tập 2: Cho elip có phương trình: . Tìm tiêu điểm và tiêu cự của elip...
Bài 7.23 trang 56 Toán 10 Tập 2: Lập phương trình chính tắc của parabol đi qua điểm M(2; 4)...
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
