Hoạt động 5 trang 52 Toán 10 Tập 2 | Kết nối tri thức Giải Toán lớp 10

Hoạt động 5 trang 52 Toán 10 Tập 2 | Kết nối tri thức Giải Toán lớp 10

Hoàng Ngân Ngày: 28-03-2023 Lớp 10

1 K

Với giải Hoạt động 5 trang 52 SGK Toán 10 Kết nối tri thức chi tiết trong Bài 22: Ba đường Conic giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 22: Ba đường Conic

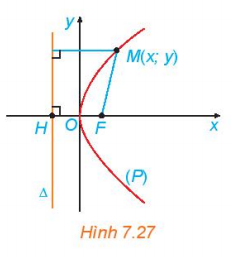
Hoạt động 5 trang 52 Toán 10 Tập 2: Xét (P) là một parabol với tiêu điểm F và đường chuẩn ∆. Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên ∆. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của HF, tia Ox trùng tia OF( H.7.27)

a) Nêu toạ độ của F và phương trình của ∆

b) Giải thích vì sao điểm M(x; y) thuộc (P) khi và chỉ khi $\sqrt{{(x - \frac{p}{2})}^{2} + y^{2}} = |x + \frac{p}{2}|$

Giải Toán 10 Bài 22 (Kết nối tri thức): Ba đường Conic (ảnh 1)

Lời giải:

a) Theo giả thiết ta có: HF = p và O là trung điểm của HF nên F $(\frac{p}{2}; 0)$ và H $(- \frac{p}{2}; 0)$

Đường thẳng ∆ đi qua điểm H $(- \frac{p}{2}; 0)$ và nhận vectơ đơn vị của trục Ox là $\vec{i}$ (1; 0) là vectơ pháp tuyến, do đó phương trình ∆ là: 1. $(x + \frac{p}{2})$ + 0.(y – 0) = 0 hay $x + \frac{p}{2}$ = 0.

Vậy F $(\frac{p}{2}; 0)$ và phương trình đường chuẩn ∆ là: $x + \frac{p}{2}$ = 0.

b)

Ta có: $\vec{F M} (x - \frac{p}{2}; y)$ ⇒ MF = $\sqrt{{(x - \frac{p}{2})}^{2} + y^{2}}$

Ta lại có: d(M, ∆) = $\frac{|x + \frac{p}{2}|}{\sqrt{1^{2} + 0^{2}}}$ = $|x + \frac{p}{2}|$

* Giả sử điểm M(x; y) thuộc (P) ta cần chứng minh: $\sqrt{{(x - \frac{p}{2})}^{2} + y^{2}} = |x + \frac{p}{2}|$

Theo giả thiết ta có điểm M(x; y) thuộc (P) nên điểm M cách đều F và ∆

⇒ MF = d(M, ∆)

⇒ $\sqrt{{(x - \frac{p}{2})}^{2} + y^{2}}$ = $|x + \frac{p}{2}|$ (đpcm)

* Giả sử với điểm M(x; y) và $\sqrt{{(x - \frac{p}{2})}^{2} + y^{2}} = |x + \frac{p}{2}|$ ta cần chứng minh: M(x; y) thuộc (P)

Theo giả thiết ta có: $\sqrt{{(x - \frac{p}{2})}^{2} + y^{2}} = |x + \frac{p}{2}|$ .

⇒ MF = d(M, ∆) hay điểm M cách đều F và ∆

⇒ M(x; y) thuộc (P). (đpcm)

Xem thêm lời giải sách giáo khoa Toán 10 Kết nối tri thức hay, chi tiết khác:

Hoạt động 1 trang 48 Toán 10 Tập 2: Đính hai đầu của một sợi dây không đàn hồi vào hai vị trí cố định F1; F2 trên một mặt bàn (độ dài sợi dây lớn hơn khoảng cách giữa hai điểm F1; F2). Kéo căng sợi dây tại một điểm M bởi một đầu bút dạ (hoặc phấn). Di chuyển đầu bút dạ để nó vẽ trên mặt bàn một đường khép kín (H.7.18)...

Câu hỏi trang 49 Toán 10 Tập 2: Tại sao trong định nghĩa elip cần điều kiện a > c?...

Luyện tập 1 trang 49 Toán 10 Tập 2: Trên bàn bida hình elip có một lỗ thu bi tại một tiêu điểm (H.7.20). Nếu gậy chơi tác động đủ mạnh vào một bi đặt tại tiêu điểm còn lại của bàn, thì sau khi vào thành bàn, bi sẽ lật lại và chạy về lỗ thu( bỏ qua các tác động phụ). Hỏi độ dài quãng đường bi lăn từ điểm xuất phát tới lỗ thu có phụ thuộc vào đường đi của bi hay không? Vì sao?...

Hoạt động 2 trang 49 Toán 10 Tập 2: Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của F1F2, tia Ox trùng tia OF2 (H.7.21)...

Luyện tập 2 trang 50 Toán 10 Tập 2: Cho elip có phương trình chính tắc: $\frac{x^{2}}{100} + \frac{y^{2}}{64} = 1$ . Tìm các tiêu điểm và tiêu cự của elip...

Vận dụng 1 trang 50 Toán 10 Tập 2: Trong bản vẽ thiết kế, vòm của ô thoáng trong Hình 7.22 là nửa nằm phía trên trục hoành của elip có phương trình $\frac{x^{2}}{16} + \frac{y^{2}}{4} = 1$ . Biết rằng 1 đơn vị trên mặt phẳng toạ độ của bản vẽ thiết kế ứng với 30cm trên thực tế. Tính chiều cao h của ô thoáng tại điểm cách điểm chính giữa của đế ô thoáng 75cm...

Hoạt động 3 trang 50 Toán 10 Tập 2: Giả sử thiết bị tại F2 nhận được tín hiệu âm thanh sớm hơn thiết bị tại F1 là 2 giây và vận tốc âm thanh là 343 m/s....

Câu hỏi trang 50 Toán 10 Tập 2: Tại sao trong định nghĩa hypebol cần điều kiện a < c?...

Luyện tập 3 trang 51 Toán 10 Tập 2: Cho hình chữ nhật ABCD và M; N tương ứng là trung điểm của các cạnh AB; CD (H.7.25). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N...

Hoạt động 4 trang 51 Toán 10 Tập 2: Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm F1F2, tia Ox trùng tia OF2 (H.7.26). Nêu toạ độ của các tiêu điểm F1; F2. Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi...

Luyện tập 4 trang 52 Toán 10 Tập 2: Cho (H) : $\frac{x^{2}}{144} - \frac{y^{2}}{25} = 1$ . Tìm các tiêu điểm và tiêu cự của (H)...

Hoạt động trang 52 Toán 10 Tập 2: Cho parabol (P): y = $\frac{1}{4} x^{2}$ . Xét F(0; 1) và đường thẳng ∆: y + 1 = 0 . Với điểm M(x; y) bất kì, chứng minh rằng MF = d(M, ∆) ⇔ M(x; y) thuộc (P)...

Hoạt động 5 trang 52 Toán 10 Tập 2: Xét (P) là một parabol với tiêu điểm F và đường chuẩn ∆. Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên ∆. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của HF, tia Ox trùng tia OF( H.7.27)...

Vận dụng 2 trang 53 Toán 10 Tập 2: Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gì? Vì sao?...

Vận dụng 3 trang 56 Toán 10 Tập 2: Gương elip trong một máy tán sỏi thận (H.7.33) ứng với elip có phương trình chính tắc $\frac{x^{2}}{400} + \frac{y^{2}}{76} = 1$ (theo đơn vị cm). Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán...

Bài 7.19 trang 56 Toán 10 Tập 2: Cho elip có phương trình: $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$ . Tìm tiêu điểm và tiêu cự của elip...

Bài 7.20 trang 56 Toán 10 Tập 2: Cho hypebol có phương trình $\frac{x^{2}}{7} - \frac{y^{2}}{9} = 1$ . Tìm tiêu điểm và tiêu cự của hypebol...

Bài 7.21 trang 56 Toán 10 Tập 2: Cho parabol có phương trình: y² = 8x. Tìm tiêu điểm và đường chuẩn của parabol...

Bài 7.22 trang 56 Toán 10 Tập 2: Lập phương trình chính tắc của elip đi qua điểm A(5; 0) và có một tiêu điểm là F2(3; 0)....

Bài 7.23 trang 56 Toán 10 Tập 2: Lập phương trình chính tắc của parabol đi qua điểm M(2; 4)...

Bài 7.24 trang 56 Toán 10 Tập 2: Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thuỷ thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác định được tàu thuỷ thuộc đường hypebol nào? Viết phương trình chính tắc của hypebol đó theo đơn vị kilômét...

Bài 7.25 trang 56 Toán 10 Tập 2: Khúc cua của một con đường có dạng hình hypebol, điểm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400m. Đỉnh parabol (P) của khúc cua cách đường thẳng AB một khoảng 20 m và cách đều A, B (H.7.34)...

Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 22: Ba đường Conic

Bài tập cuối chương 7

Bài 23: Quy tắc đếm

Bài 24: Hoán vị, chỉnh hợp và tổ hợp

Từ khóa :

Ba đường conic toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

169

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

116

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.