Với giải Vận dụng trang 45 SGK Toán 10 Kết nối tri thức chi tiết trong Bài 21: Đường tròn trong mặt phẳng tọa độ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 21: Đường tròn trong mặt phẳng tọa độ

Vận dụng trang 45 Toán 10 Tập 2: Bên trong một hồ bơi, người ta dự định thiết kế hai bể sục nửa hình tròn bằng nhau và một bể sục hình tròn (H.7.14) để người bơi có thể ngồi dựa lưng vào thành các bể sục thư giãn. Hãy tìm bán kính của các bể sục để tổng chu vi của ba bể là 32 m mà tổng diện tích (chiếm hồ bơi) là nhỏ nhất. Trong tính toán, lấy π ≈ 3,14, độ dài tính theo mét và làm tròn tới chữ số thập phân thứ hai

Lời giải:

Gọi x và y (m) lần lượt là bán kính của bể hình tròn và bể nửa hình tròn

Chu vi một nửa hình tròn bán kính y là: πy + 2y = (π + 2)y (m)

Khi đó chu vi của hai nửa hình tròn bán kính y là: 2(π + 2)y (m)

Chu vi của hình tròn bán kính x là: 2πx (m)

Theo giả thiết tổng chu vi của ba bể là 32 m nên 2πx + 2(π + 2)y = 32

                                                                        hay 1,57x + 2,57y – 8 = 0

Gọi tổng diện tích ba bể sục là S (m2). Khi đó: πx2 + πy2 = S

⇒ x2 + y2 = $\frac{S}{\pi }$= $\frac{S}{\mathrm{3,14}}$.

Trong hệ trục toạ độ Oxy xét đường tròn (C) : x2 + y2 = $\frac{S}{\mathrm{3,14}}$ có tâm O(0; 0), bán kính R = $\sqrt{\frac{S}{\mathrm{3,14}}}$ và đường thẳng ∆: 1,57x + 2,57y – 8 = 0

Để S là nhỏ nhất thì khi đó bài toán trở thành: Tìm R nhỏ nhất để (C) và ∆ có ít nhất một điểm chung với hoành độ và tung độ đều là các số dương

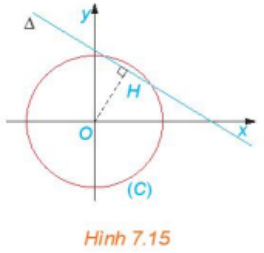
Để (C) và d có ít nhất một điểm chung thì d(O; ∆) ≤ R

Ta có: d((O; ∆) = $\frac{\left|\mathrm{1,57.0}+\mathrm{2,57.0}–8\right|}{\sqrt{{\left(\mathrm{1,57}\right)}^2+{\left(\mathrm{2,57}\right)}^2}}$ ≈ 2,66  ⇒ R ≥ 2,66

Dấu “=” xảy ra khi đường tròn (C) tiếp xúc với đường thẳng ∆. Do đó, GTNN của R = 2,66

Do đó, ta có hệ phương trình sau: $\left\{\begin{array}{l}\mathrm{1,57}x+\mathrm{2,57}y-8=0\left(1\right)\\ x^2+y^2={\mathrm{2,66}}^2\left(2\right)\end{array}\right.$

Từ phương trình (1) ta có:  $x=\frac{8-\mathrm{2,57}y}{\mathrm{1,57}}$

Thay x vào phương trình (2) ta được: ${\left(\frac{8-\mathrm{2,57}y}{\mathrm{1,57}}\right)}^2+y^2={\mathrm{2,66}}^2$ 

⇔ 2,572.y2 – 2.8.2,57.y + 82 + 1,572.y2 = 2,662.1,572

⇔ $({\mathrm{2,57}}^2+{\mathrm{1,57}}^2)y^2-\mathrm{2.8.2,57}y+64-{\mathrm{2,66}}^2{\mathrm{.1,57}}^2=0$

⇔ $\left[\begin{array}{l}{y}_1\approx \mathrm{2,34}\\ y_2\approx \mathrm{2,19}\end{array}\right.\Rightarrow \left[\begin{array}{l}{x}_1\approx \mathrm{1,27}\\ x_2\approx \mathrm{1,51}\end{array}\right.$

Vậy để diện tích của các bể sục là nhỏ nhất thì bán kính của bể hình tròn và bể nửa hình tròn lần lượt là 1, 27m và 2,34m hoặc 1,51 m và 2,19 m