Với giải Câu 2 trang 103 Vở bài tập Toán lớp 7 Cánh diều chi tiết trong Bài 9: Đường trung trực của một đoạn thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 7. Mời các bạn đón xem:

Giải VBT Toán lớp 7 Bài 9: Đường trung trực của một đoạn thẳng

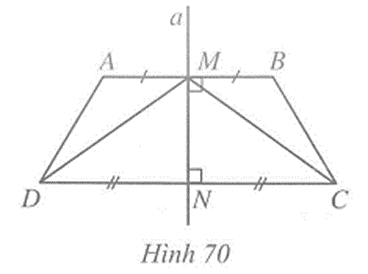
Câu 2 trang 103 vở bài tập Toán lớp 7 Tập 2: Trong Hình 70 đường thẳng a là đường trung trực của đoạn thẳng AB và CD. Chứng minh:

a) AB // CD;

b) ∆MNC = ∆MND;

c) $\widehat{\mathrm{AMD}}$= $\widehat{\mathrm{BMC}}$;

d) AD = BC, $\hat{A}$= $\hat{B}$;

e) $\widehat{\mathrm{ADC}}$= $\widehat{\mathrm{BCD}}$.

Lời giải:

a) Vì a là đường trung trực của cả hai đoạn thẳng AB và CD nên AB $\perp$ a; CD $\perp$ a. Suy ra AB // CD.

b) Xét hai tam giác vuông MNC và MND, ta có:

NC = ND (giả thiết); MN là cạnh chung.

Suy ra ∆MNC = ∆MND (cạnh huyền – cạnh góc vuông).

c) Vì ∆MNC = ∆MND nên $\widehat{\mathrm{DMN}}$ = $\widehat{\mathrm{CMN}}$(1)

Ta có: $\widehat{\mathrm{AMD}}$và $\widehat{\mathrm{DMN}}$, $\widehat{\mathrm{BMC}}$và $\widehat{\mathrm{CMN}}$ là các cặp góc kề nhau; $\widehat{\mathrm{AMN}}$ = $\widehat{\mathrm{BMN}}$ = 90^o

Suy ra $\widehat{\mathrm{AMD}}$+ $\widehat{\mathrm{DMN}}$ = $\widehat{\mathrm{AMN}}$= 90^o và $\widehat{\mathrm{BMC}}$ + $\widehat{\mathrm{CMN}}$= $\widehat{\mathrm{BMN}}$= 90^o

Do đó $\widehat{\mathrm{AMD}}$= 90^o – $\widehat{\mathrm{DMN}}$và $\widehat{\mathrm{BMC}}$= 90^o – $\widehat{\mathrm{CMN}}$(2)

Từ (1) và (2) suy ra $\widehat{\mathrm{AMD}}$= $\widehat{\mathrm{BMC}}$

d) Vì ∆MNC = ∆MND nên MC = MD

Xét hai tam giác AMD và BMC, ta có:

AM = BM (giả thiết), $\widehat{\mathrm{AMD}}$= $\widehat{\mathrm{BMC}}$, MD = MC (chứng minh ở trên)

Suy ra ∆AMD = ∆BMC (c.g.c)

Do đó AD = BC ( hai cạnh tương ứng); $\hat{A}$= $\hat{B}$ (hai góc tương ứng)

e) Vì ∆MNC = ∆MND nên $\widehat{\mathrm{MCN}}$= $\widehat{\mathrm{MDN}}$ (hai góc tương ứng)

Vì ∆BMC = ∆AMD nên $\widehat{\mathrm{BCM}}$= $\widehat{\mathrm{ADM}}$ (hai góc tương ứng)

Suy ra $\widehat{\mathrm{MCN}}$+ $\widehat{\mathrm{BCM}}$ = $\widehat{\mathrm{MDN}}$ + $\widehat{\mathrm{ADM}}$

Mà $\widehat{\mathrm{MCN}}$và $\widehat{\mathrm{BCM}}$, $\widehat{\mathrm{MDN}}$và $\widehat{\mathrm{ADM}}$ là các cặp góc kề nhau nên từ đó suy ra: $\widehat{\mathrm{ADC}}=\widehat{\mathrm{BCD}}$