Với Giải toán 10 trang 102 Tập 1 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải toán 10 trang 102 Tập 1 Chân trời sáng tạo
Bài 1 trang 102 Toán lớp 10: Cho ba vectơ đều khác vectơ . Các khẳng định sau đúng hay sai?
a) Nếu hai vectơ cùng phương với thì và cùng phương.
b) Nếu hai vectơ cùng ngược hướng với thì và cùng hướng.
Phương pháp giải:
Nhận xét về giá và hướng của hai vectơ với vectơ để rút ra kết luận.
Lời giải:
a)
+) Vectơ cùng phương với vectơ nên giá của vectơ song song với giá của vectơ
+) Vectơ cùng phương với vectơ nên giá của vectơ song song với giá của vectơ
Suy ra giá của vectơ và vectơ song song với nhau nên và cùng phương
Vậy khẳng định trên đúng
b) Giả sử vectơ có hướng từ A sang B
+) Vectơ ngược hướng với vectơ nên giá của vectơ song song với giá của vectơ và có hướng từ B sang A
+) Vectơ ngược hướng với vectơ nên giá của vectơ song song với giá của vectơ và có hướng từ B sang A
Suy ra, hai vectơ và cùng hướng
Vậy khẳng định trên đúng
Bài 2 trang 102 Toán lớp 10: Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.
a) Tính độ dài của các vectơ .
b) Tìm trong hình các cặp vectơ đối nhau và có độ dài bằng .
Phương pháp giải:
a) Bước 1: Tính độ dài AC, BD
Bước 2: Tính độ dài vectơ
b) Bước 1: Tìm các đoạn thẳng có độ dài là
Bước 2: Từ các đoạn thẳng trên xác định các vecto cùng phương (giá song song hoặc trùng nhau) nhưng ngược hướng.
Lời giải:
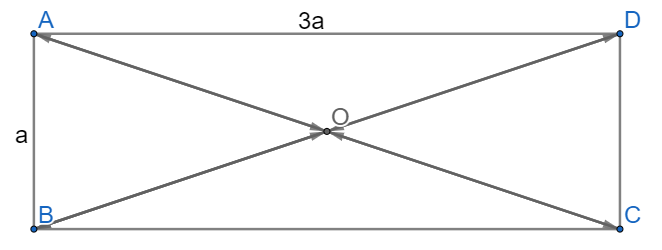
a) Ta có:
+)
+)
b) O là giao điểm của hai đường chéo nên ta có:
Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng
Suy ra các cặp vectơ đối nhau và có độ dài bằng là:
và ; và ; và ; và
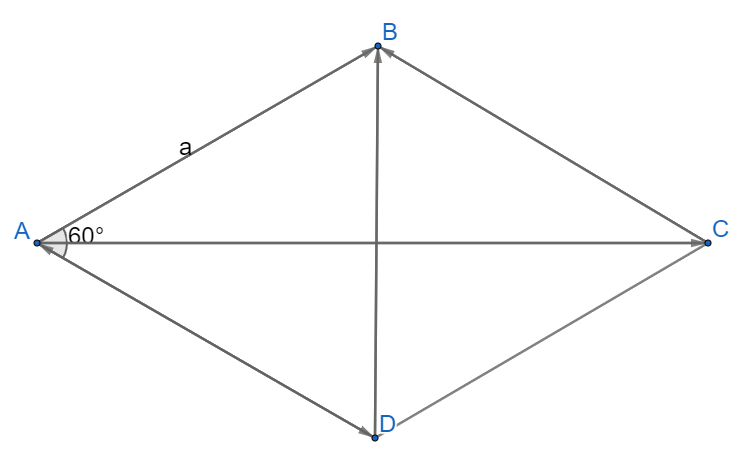
Bài 3 trang 102 Toán lớp 10: Cho hình thoi ABCD đi có cạnh bằng a và có góc A bằng . Tìm độ dài của các vectơ sau: .
Phương pháp giải:
Quy tắc ba điểm
Quy tắc hình bình hành (với ABCD là hình bình hành);
Quy tắc hiệu:
Áp dụng các quy tắc trên để xác định vecto rồi tính độ dài.
Lời giải:
+) ABCD là hình thoi nên cũng là hình bình hành
Áp dụng quy tắc hình bình hành ta có:
+)
+)
Bài 4 trang 102 Toán lớp 10: Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho (Hình 1).
a) Tìm tổng của các vectơ và ; và ; và .
b) Tìm các vectơ hiệu: .
c) Chứng minh .
Phương pháp giải:
a) Chỉ ra các hình bình hành, từ đó suy ra các vectơ bằng nhau và vận dụng quy tắc hình bình hành.
b) Quy tắc hiệu: , quy tắc ba điểm và thay thế các vectơ bằng nhau
c) Thay thế các vectơ bằng nhau ; sử dụng quy tắc hình bình hành (với ABCD là hình bình hành)
Lời giải:
a) Ta có: và
Suy ra
+)
+) ABCD là hình bình hành nên
+) Ta có là hình bình hành nên
(vì AMED là hình bình hành)
b) Ta có:
+)
+)
+)
c) Ta có:
Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có
Từ đó suy ra (đpcm)
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Giải toán lớp 10 trang 103 Tập 1