Với Giải toán lớp 7 trang 96 Tập 2 Cánh diều tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải Toán 7 trang 96 Tập 2 Cánh diều

Bài 1 trang 96 Toán 7 Tập 2: Cho tam giác ABC cân tại A có M là trung điểm của cạnh AC và N là trung điểm của cạnh AB. Chứng minh BM = CN.

Lời giải:

Chứng minh (Hình vẽ dưới đây)

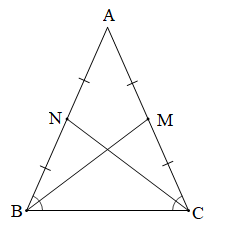
Tam giác ABC cân tại A (giả thiết) nên $\widehat{B}=\widehat{C}$ và  AB = AC (1)

Mà M là trung điểm cạnh AC (giả thiết) nên AM = MC $=\frac{1}{2}AC$ (2)

N là trung điểm cạnh AB (giả thiết) nên AN = NB $=\frac{1}{2}AB$ (3)

Từ (1), (2) và (3) suy ra AM = MC = AN = NB

 Xét tam giác BNC và tam giác CMB có:

BN = CM (chứng minh trên)

$\widehat{B}=\widehat{C}$(chứng minh trên)

BC là cạnh chung

Do đó $∆$BNC = $∆$CMB (c.g.c)

Suy ra CN = BM (hai cạnh tương ứng)

Vậy BM = CN.

Bài 2 trang 96 Toán 7 Tập 2: Cho tam giác ABC có $\widehat{A}=120°.$ Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.

Lời giải:

Chứng minh (Hình vẽ dưới đây)

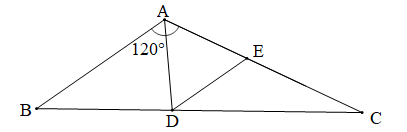
Vì AD là tia phân giác góc A (giả thiết)

Nên $\widehat{BAD}=\widehat{CAD}=\frac{1}{2}\widehat{BAC}$ (tính chất tia phân giác của một góc)

Mà $\widehat{BAC}=120°$ nên $\widehat{BAD}=\widehat{CAD}=\frac{1}{2}\widehat{BAC}=\frac{1}{2}.120°=60°$ 

Lại có DE // AB (giả thiết) nên $\widehat{ADE}=\widehat{BAD}=60°$ (hai góc so le trong)

Do đó tam giác ADE có $\widehat{DAE}=\widehat{ADE}=60°$ 

Suy ra tam giác ADE là tam giác cân có một góc bằng 60°.

Suy ra tam giác ADE là tam giác đều.

Vậy tam giác ADE là tam giác đều.

Bài 3 trang 96 Toán 7 Tập 2: Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.

Lời giải:

Chứng minh (Hình vẽ dưới đây)

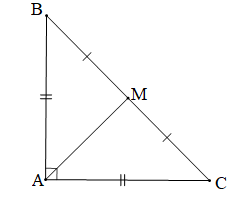
+) Tam giác ABC là tam giác vuông cân tại A (giả thiết) nên AB = AC và $\widehat{A}=90°,$ $\widehat{B}=\widehat{C}=45°$ 

Xét tam giác ABM và tam giác ACM có:

AM là cạnh chung

MB = MC (M là trung điểm của BC)

AB = AC (chứng minh trên)

Do đó $∆$ABM = $∆$ACM (c.c.c)

Suy ra $\widehat{BAM}=\widehat{CAM}$ (hai góc tương ứng)

Nên tia AM là tia phân giác của góc A

Do đó $\widehat{BAM}=\widehat{CAM}=\frac{1}{2}.\widehat{A}=\frac{1}{2}.90°=45°$

+) Xét tam giác MAB có $\widehat{B}=45°,\widehat{BAM}=45°$ 

Do đó tam giác MAB cân tại M. (1)

Lại có $\widehat{BMA}=\widehat{CMA}$ (hai góc tương ứng của $∆$ABM = $∆$ACM)

Mà $\widehat{BMA}+\widehat{CMA}=180°$(tính chất hai góc kề bù)

Do đó $\widehat{BMA}=\widehat{CMA}=\frac{1}{2}.180°=90°$

Nên tam giác MAB vuông tại M. (2)

Từ (1) và (2) suy ra tam giác MAB vuông cân tại M.

Bài 4 trang 96 Toán 7 Tập 2: Trong Hình 76, cho biết các tam giác ABD và BCE là các tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:

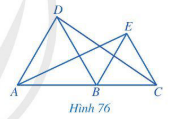
a) AD // BE và BD // CE;

b) $\widehat{ABE}=\widehat{DBC}=120°;$ 

c) AE = CD.

Lời giải:

Chứng minh (Hình 76):

a) Vì tam giác ABD đều (giả thiết)

Nên AB = BD = AD và $\widehat{DAB}=\widehat{DBA}=\widehat{ADB}=60°$ 

Tam giác BCE đều (giả thiết)

Nên BC = CE = BE và $\widehat{ECB}=\widehat{EBC}=\widehat{CEB}=60°$ 

Vì $\widehat{DAB}=\widehat{EBC}\left(=60°\right)$ mà hai góc này ở vị trí đồng vị

Nên AD // BE (dấu hiệu nhận biết hai đường thẳng song song)

Vì $\widehat{DBA}=\widehat{ECB}\left(=60°\right)$ mà hai góc này ở vị trí đồng vị

Nên BD // CE (dấu hiệu nhận biết hai đường thẳng song song)

Vậy AD // BE và BD // CE.

b) Vì $\widehat{ABE}$ và $\widehat{EBC}$ là hai góc kề bù nên $\widehat{ABE}+\widehat{EBC}=180°$ (tính chất hai góc kề bù)

Suy ra $\widehat{ABE}=180°-\widehat{EBC}=180°-60°=120°$

Tương tự ta cũng có $\widehat{DBA}+\widehat{DBC}=180°$ (tính chất hai góc kề bù)

Nên $\widehat{DBC}=180°-\widehat{DBA}=180°-60°=120°$

Vậy $\widehat{ABE}=\widehat{DBC}=120°.$

c) Xét tam giác ABE và tam giác DBC có:

AB = DB (chứng minh trên)

$\widehat{ABE}=\widehat{DBC}\left(=120°\right)$ (chứng minh trên)

BE = BC (chứng minh trên)

Do đó $∆$ABE = $∆$DBC (c.g.c)

Suy ra AE = CD (hai cạnh tương ứng)

Vậy AE = CD.

Bài 5 trang 96 Toán 7 Tập 2: Trong thiết kế của một ngôi nhà, độ nghiêng của mái nhà so với phương nằm ngang phải phù hợp với kết cấu của ngôi nhà và vật liệu làm mái nhà. Hình 77 mô tả mặt cắt đứng của ngôi nhà, trong đó độ nghiêng của mái nhà so với phương nằm ngang được biểu diễn bởi số đo góc ở đáy của tam giác ABC cân tại A.

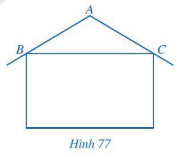
Tính độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong mỗi trường hợp sau:

a) Góc ở đỉnh A là (khoảng) 120° đối với mái nhà lợp bằng ngói;

b) Góc ở đỉnh A là (khoảng) 140° đối với mái nhà lợp bằng fibro xi măng;

c) Góc ở đỉnh A là (khoảng) 148° đối với mái nhà lợp bằng tôn.

Lời giải:

Tam giác ABC cân tại A nên $\widehat{B}=\widehat{C}$ 

Xét tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng ba góc trong một tam giác)

Suy ra $\widehat{A}+\widehat{B}+\widehat{B}=180°$ 

Hay $2\widehat{B}=180°-\widehat{A}$ 

Do đó $\widehat{B}=\widehat{C}=\frac{180°-\widehat{A}}{2}$

a) Góc ở đỉnh A là (khoảng) 120° đối với mái nhà lợp bằng ngói nên $\widehat{A}=120°$ 

Do đó $\widehat{B}=\widehat{C}=\frac{180°-120°}{2}=30°$

Vậy độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong trường hợp này là 30°.

b) Góc ở đỉnh A là (khoảng) 140° đối với mái nhà lợp bằng fibro xi măng nên $\widehat{A}=140°$ 

Do đó $\widehat{B}=\widehat{C}=\frac{180°-140°}{2}=20°$

Vậy độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong trường hợp này là 20°.

c) Góc ở đỉnh A là (khoảng) 148° đối với mái nhà lợp bằng tôn nên $\widehat{A}=148°$

Do đó $\widehat{B}=\widehat{C}=\frac{180°-148°}{2}=16°$

Vậy độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong trường hợp này là 16°.

Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:

Giải Toán 7 trang 93 Tập 2

Giải Toán 7 trang 94 Tập 2

Giải Toán 7 trang 95 Tập 2