Với Giải toán lớp 7 trang 91 Tập 2 Cánh diều tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải Toán 7 trang 91 Tập 2 Cánh diều
Bài 1 trang 91 Toán 7 Tập 2: Cho hai tam giác ABC và A'B'C' thỏa mãn: AB = A'B', , . Hai tam giác ABC và A'B'C' có bằng nhau không? Vì sao?
Lời giải:
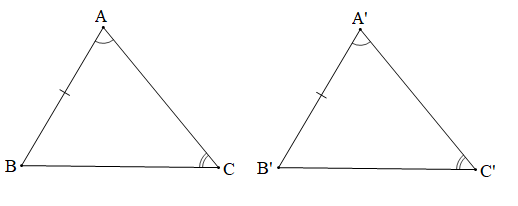
|
GT |
ABC, A'B'C', AB = A'B', |
|
KL |
ABC và A'B'C' có bằng nhau không? Vì sao? |
Xét tam giác ABC có: (tổng ba góc trong một tam giác)
Suy ra: .
Xét tam giác A'B'C' có: (tổng ba góc trong một tam giác)
Suy ra: .
Mà , (giả thiết) nên .
Xét ABC và A'B'C' có:
(giả thiết),
AB = A’B’ (giả thiết),
(giả thiết).
Suy ra ABC = A'B'C' (g.c.g).
Vậy ABC = A'B'C'.
Bài 2 trang 91 Toán 7 Tập 2: Cho Hình 65 có AM = BN, .
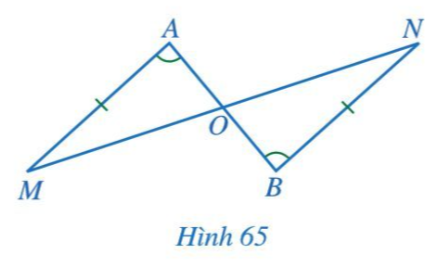
Chứng minh: OA = OB, OM = ON.
Lời giải:
|
GT |
AMO, BNO, AM = BN, . |
|
KL |
OA = OB, OM = ON. |
Chứng minh (Hình 65):
Xét AMO có: (tổng ba góc trong một tam giác)
Suy ra: . (1)
Xét BNO có: (tổng ba góc trong một tam giác)
Suy ra: . (2)
Mà (theo giả thiết), (hai góc đối đỉnh) (3)
Từ (1), (2) và (3) ta có: .
Xét AMO và BNO có:
(giả thiết).
AM = BN (giả thiết).
(chứng minh trên).
Suy ra AMO và BNO (g.c.g).
Do đó OA = OB và OM = ON (các cặp cạnh tương ứng).
Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác: