Với Giải toán 10 trang 66 Tập 1 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải toán 10 trang 66 Tập 1 Chân trời sáng tạo

HĐ Khám phá 1 trang 66 Toán lớp 10: a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và $\hat{C}\ge \hat{B}.$ Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.

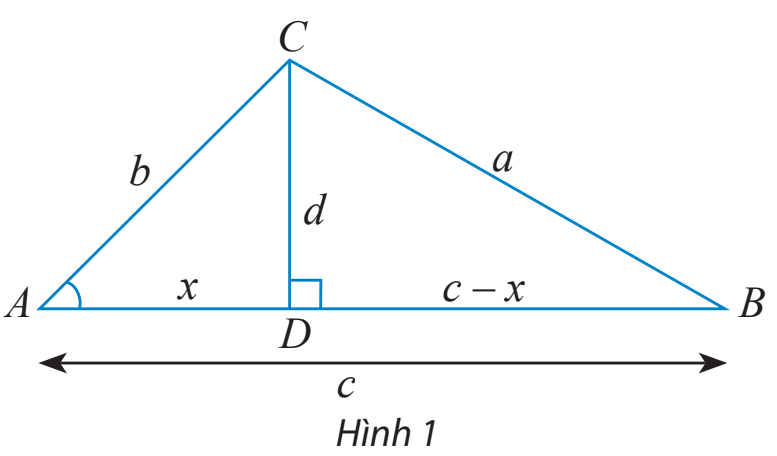
Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức $a^2=b^2+c^2-2bc\cos A$ theo gợi ý sau:

Xét tam giác vuông BCD, ta có: $a^2=d^2+(c-x{)}^2=d^2+x^2+c^2-2xc$    (1)

Xét tam giác vuông ACD, ta có: $b^2=d^2+x^2\Rightarrow d^2=b^2-x^2$    (2)

$\cos A=\frac{?}{b}\Rightarrow ?=b\cos A.$     (3)                   

Thay (2) và (3) vào (1), ta có: $a^2=b^2+c^2-2bc\cos A$

Lưu ý: Nếu $\hat{B}>\hat{C}$ thì ta vẽ đường cao BD và chứng minh tương tự.

b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:

$a^2=b^2+c^2-2bc\cos A$

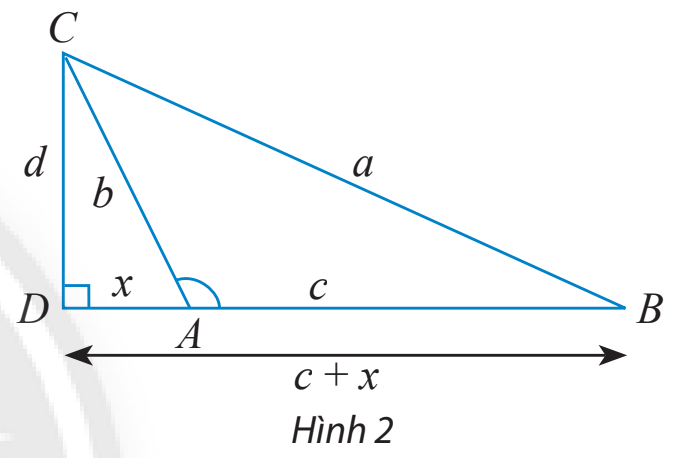
Lưu ý: Vì A là góc tù nên $\cos A=-\frac{x}{b}.$

c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức $a^2=b^2+c^2-2bc\cos A$ có thể viết là $a^2=b^2+c^2.$

Lời giải:

a) ? = x vì $\cos A=\frac{AD}{AC}=\frac{x}{b}\Rightarrow ?=x.$

b) Xét tam giác vuông BCD, ta có: $a^2=d^2+(c+x{)}^2=d^2+x^2+c^2+2xc$          (1)

Xét tam giác vuông ACD, ta có: $b^2=d^2+x^2\Rightarrow d^2=b^2-x^2$    (2)

$\cos A=-\cos \widehat{DAC}=-\frac{x}{b}\Rightarrow x=-b\cos A.$    (3)         

Thay (2) và (3) vào (1), ta có: $a^2=b^2+c^2-2bc\cos A$

c) Ta có: $a^2=b^2+c^2-2bc\cos A$

Mà $\hat{A}={90}^o\Rightarrow \cos A=\cos {90}^o=0.$

$\Rightarrow a^2=b^2+c^2$

Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Giải toán lớp 10 trang 65 Tập 1

Giải toán lớp 10 trang 67 Tập 1

Giải toán lớp 10 trang 69 Tập 1

Giải toán lớp 10 trang 70 Tập 1

Giải toán lớp 10 trang 71 Tập 1

Giải toán lớp 10 trang 72 Tập 1

Giải toán lớp 10 trang 73 Tập 1