Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 7 Chương 2: Số thực sách Cánh diều. Bài viết gồm 30 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 7.
Trắc nghiệm Toán 7 Chương 2: Số thực
Câu 1. Giá trị thoả mãn là:
A. x = −1;
B. x = 0;
C. x = −1 hoặc x = 0;
D. x = 1;
Đáp án đúng là: B.
Ta có
Hay
Do đó giá trị x nguyên thoả mãn là x = 0.
Câu 2. Kết quả của phép tính là:
A. ;
B.
C.
D.
Đáp án đúng là: B.
Câu 3. Cho Giá trị x thoả mãn là:
A. x = −10;
B. x = 10;
C. x = 3,6;
D. x = −3,6.
Đáp án đúng là: B.
Từ tỉ lệ thức ta có 9x = (−6).(−15)
Do đó 9x = 90.
Suy ra x = 90 : 9
x = 10.
Vậy x = 10.
Câu 4. Tổng các giá trị của x thoả mãn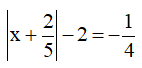
A.
B.
C.
D.
Đáp án đúng là: C.
Trường hợp 1:
Trường hợp 2:
Vậy có hai giá trị x thoả mãn là ; .
Tổng của hai giá trị x tìm được ở trên là:
Vậy tổng của các giá trị x là
Câu 5. Giá trị nhỏ nhất của biểu thức A = |2x – 1| + 5 là:
A. 0;
B. 4;
C. 5;
D. 6.
Đáp án đúng là: C.
Ta có |2x – 1| ≥ 0 với mọi x nên |2x – 1| + 5 ≥ 5 với mọi x
Do đó A đạt giá trị nhỏ nhất là 5 khi 2x – 1= 0 tức là 2x = 1 hay
Vậy giá trị nhỏ nhất của A là 5.
Câu 6. Trong các phát biểu sau, phát biểu nào sai?
A. Nếu thì a không thể là số vô tỉ;
B. Nếu thì a không thể là số vô tỉ;
C. Nếu thì a không thể là số vô tỉ;
D. Nếu thì a không thể là số vô tỉ;
Đáp án đúng là: D.
Tập hợp ℚ là tập hợp các số hữu tỉ nên không thể là số vô tỉ. Do đó phương án A là phát biểu đúng.
Tập hợp ℤ là tập hợp các số nguyên nên không thể là số vô tỉ. Do đó phương án B là phát biểu đúng.
Tập hợp ℕ là tập hợp các số tự nhiên nên không thể là số vô tỉ. Do đó phương án C là phát biểu đúng.
Tập hợp ℝ là tập hợp các số thực, bao gồm các số vô tỉ. Do đó phương án D là phát biểu sai.
Câu 7. Giá trị của biểu thức là:
A. 0;
B.
C.
D.
Đáp án đúng là: B.
= (–12) : 0,6 + 7,2
Vậy giá trị của biểu thức là .
Câu 8. Có bao nhiêu giá trị của x thoả mãn ?
A. 0;
B. 1;
C. 2;
D. 311.
Đáp án đúng là: B.
Ta có:
Suy ra
Do đó 2x + 3= 625
2x = 625 – 3
2x = 622
x = 311.
Vậy có 1 giá trị của x thoả mãn.
Câu 9. Thực hiện phép tính |–3,7| + 6,3 + |–1,4| – |3,7| – |6,3| ta được kết quả là:
A. –1,4;
B. 1,4;
C. 21,4;
D. 18,6.
Đáp án đúng là: B.
|–3,7| + 6,3 + |–1,4| – |3,7| – |6,3|
= –(–3,7) + 6,3 + [–(–1,4)] – 3,7 – 6,3
= 3,7 + 6,3 + 1,4 – 3,7 – 6,3
= (3,7 + 6,3) + 1,4 – (3,7 + 6,3)
= 10 + 1,4 – 10
= (10 – 10) + 1,4
= 0 + 1,4
= 1,4.
Câu 10. Điểm nào trên trục số biểu diễn giá trị x thoả mãn |x| = ?
A. Điểm A;
B. Điểm B;
C. Điểm O;
D. Điểm A và điểm B.
Đáp án đúng là: D.
Ta có |x| =
Nên hoặc
Số được biểu diễn bởi điểm B trên trục số, số - được biểu diễn bởi điểm A trên trục số.
Do đó điểm A và điểm B biểu diễn giá trị x thoả mãn |x| = .
Câu 11. Viết số dưới dạng luỹ thừa của an ta được:
A. 93;
B. 95;
C. 34;
D. 35.
Đáp án đúng là: C.
Ta có:
Vậy viết dưới dạng luỹ thừa của an ta được 34 hoặc 92.
Câu 12. Sắp xếp các số −1,2; 0; ; ; 2 theo thứ tự tăng dần là:
A. −1,2; ; 0; ; 2;
B. ; −1,2; 0; ; 2;
C. ; −1,2; 0; 2; ;
D. −1,2; ; 0; ; 2.
Đáp án đúng là: D.
Ta chia các số −1,2; 0; ; ; 2 thành 3 nhóm:
Nhóm 1 gồm các số −1,2; .
Nhóm 2 là số 0.
Nhóm 3 gồm các số ; 2.
Ta so sánh nhóm 1: −1,2; .
Vì −1 > −2 nên do đó .
Mà −1 > −1,2
Vậy −1,2 < .
Ta so sánh nhóm 3: ;2.
Ta có
Vì 1,732050… < 2 nên .
Nhóm 1 gồm các số thực âm, nhóm 3 gồm các số thực dương mà số 0 luôn lớn hơn số thực âm và nhỏ hơn số thực dương.
Do đó ta có −1,2 < < 0 < .
Vậy sắp xếp theo thứ tự tăng dần ta có: −1,2; ; 0; ; 2.
Câu 13. Kết quả của phép tính là:
A. 1,3;
B. −1,3;
C. 2,9;
D. −2,9.
Đáp án đúng là: B.
Ta có
= −2,1 + 0,8
= −1,3.
Câu 14. Từ bốn số 2; 14; 0,25 và 1,75 ta lập được tỉ lệ thức là:
A. ;
B. ;
C. ;
D.
Đáp án đúng là: A.
và 0,25 : 1,75 = ;
Do đó nên từ bốn số 2; 14; 0,25 và 1,75 lập được thành tỉ lệ thức là:
; ;; .
Vậy .
Câu 15. Số thực dương thích hợp điền vào ? trong tỉ lệ thức là:
A. 64;
B. 32;
C. 8;
D. –8 hoặc 8.
Đáp án đúng là: D.
Gọi số thực dương cần tìm là x (x > 0).
Từ tỉ lệ thức ta có
Suy ra x.x = 4. 16
Hay x2 = 64
x2 = 82 = (–8)2
Mà x > 0 nên x = 8.
Vậy số cần điền là 8.
Câu 16. Cho (với a + b + c + d ≠ 0) thì:
A. a = b;
B. b = c;
C. a = c;
D. a = d.
Đáp án đúng là: C.
Từ tỉ lệ thức , áp dụng tính chất tỉ lệ thức ta có:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra:
+) do đó d + a = c + d nên a = c;
+) do đó b + c = a + b nên c = a.
Vậy a = c.
Câu 17. Cho Chọn câu đúng:
A. ;
B. ;
C. ;
D. ;
Đáp án đúng là: C.
Từ tỉ lệ thức , áp dụng tính chất tỉ lệ thức ta có:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra do đó
Câu 18. Giá trị của x, y, z thoả mãn và 4x – 3y + 2z = 36 là:
A. x = 9; y = 18; z = 27;
B. x = −9; y = −18; z = −27;
C. x = −9; y = 18; z = 27;
D. x = −9; y = 18; z = −27.
Đáp án đúng là: A.
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra:
+) x = 9;
+) do đó y = 9.2 hay y = 18;
+) do đó z = 9.3 hay z = 27.
Vậy x = 9; y = 18; z = 27.
Câu 19. Khẳng định nào dưới đây thể hiện hai đại lượng tỉ lệ thuận với nhau?
A. Chiều dài và chiều rộng của hình chữ nhật có diện tích cho trước;
B. Năng suất lao động và thời gian để làm xong một công việc;
C. Vận tốc và thời gian khi đi trên cùng một quãng đường;
D. Chu vi và bán kính của một đường tròn.
Đáp án đúng là: D.
Công thức tính diện tích hình chữ nhật có chiều dài a và chiều rộng b là S = a.b. Do đó chiều dài và chiều rộng của hình chữ nhật có diện tích cho trước là hai đại lượng tỉ lệ nghịch.
Năng suất lao động và thời gian để làm xong một công việc là hai đại lượng tỉ lệ nghịch.
Công thức tính quãng đường khi di chuyển với vận tốc v và thời gian t là S = vt, do đó vận tốc và thời gian khi đi trên cùng một quãng đường là hai đại lượng tỉ lệ nghịch.
Công thức tính chu vi C của đường tròn có bán kính R là C = π.2R nên chu vi đường tròn tỉ lệ thuận với bán kính R theo hệ số tỉ lệ là π. Do đó phương án D là đúng.
Câu 20. Chọn câu đúng.
Cho biết 9x = 5y và 3x – 2y = 12. Giá trị x và y là:
A. x = 5; y = 9;
B. x = 2; y = 3;
C. x = − 20; y = −36;
D. x = 20; y = 36.
Đáp án đúng là: C.
Từ đẳng thức 9x = 5y suy ra tỉ lệ thức .
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Do đó:
+) do đó x = (−4).5 = −20;
+) do đó y = (−4).9 = −36.
Vậy x = − 20; y = −36.
Câu 21. Cho biết x và y là hai đại lượng tỉ lệ thuận. Biết hai giá trị x1, x2 của x có tổng bằng 6 thì hai giá trị tương ứng y1, y2 của y có tổng bằng – 2. Hai đại lượng x và y liên hệ với nhau bằng công thức nào?
A. y = 3x;
B. y = −x;
C.
D. .
Đáp án đúng là: D.
Giả sử y tỉ lệ thuận với x theo hệ số tỉ kệ k (k ≠ 0), khi đó ta có y = k.x.
Áp dụng tính chất của hai đại lượng tỉ lệ thuận ta có
Áp dụng tính chất dãy tỉ số bằng nhau ta có: .
Vậy
Do đó hai đại lượng x và y liên hệ với nhau bởi công thức .
Câu 22. Cứ 100 kg thóc thì cho 65 kg gạo. Hỏi 3 tấn thóc thì cho số kg gạo là:
A. 1950 kg;
B. 0,65 tấn;
C. 35 kg;
D. 6500 kg.
Đáp án đúng là: A.
Vì khối lượng gạo y (kg) tỉ lệ thuận với khối lượng thóc x (kg) nên ta có y = kx.
Khi x = 100 thì y = 65 nên 65 = k.100
Do đó .
Vậy y = 0,65x
Đổi 3 tấn = 3 000 kg.
Với x = 3 000 thì y = 0,65.3000 = 1950 (kg).
Vậy với 3 tấn thóc thì cho 1950 kg gạo.
Câu 23. Đại lượng y tỉ lệ nghịch với đại lượng x nếu:
A. x = ay với hằng số a ≠ 0;
B. với hằng số a ≠ 0;
C. y = ax với hằng số a ≠ 0;
D. với hằng số a ≠ 0.
Đáp án đúng là: B.
Khái niệm hai đại lượng tỉ lệ nghịch:
Nếu đại lượng y liên hệ với đại lượng x theo công thức hay xy = a (với a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Câu 24. Ba đơn vị kinh doạn A, B, C góp vốn theo tỉ lệ 2; 4; 6. Sau một năm thu được tổng 1 tỉ 800 triệu đồng tiền lãi. Hỏi đơn vị B được chia bao nhiêu tiền lãi biết tiền lãi được chia tỉ lệ thuận với số vốn đã góp.
A. 150 triệu đồng;
B. 300 triệu đồng;
C. 600 triệu đồng;
D. 900 triệu đồng.
Đáp án đúng là: C.
Gọi số tiền lãi của ba đơn vị A, B, C được chia lần lượt là x, y, z (triệu đồng) (x, y, z > 0).
Theo đề bài số tiền lãi của ba đơn vị được chia lần lượt tỉ lệ với vốn đã góp là 2; 4; 6 nên ta có: .
Tổng số tiền lãi là 1 tỉ 800 triệu đồng nên x + y + z = 1800 (triệu đồng)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra: do đó y = 150.4 hay y = 600.
Vậy số tiền lãi của đơn vị B là 600 triệu đồng.
Câu 25. Bác Linh định mua 15 gói bánh với số tiền định trước. Nhưng khi đến siêu thị vào ngày lễ thì giá bánh tăng 25%. Hỏi với số tiền định trước đó thì chị Linh mua được bao nhiêu gói bánh?
A. 8 gói;
B. 10 gói;
C. 12 gói;
D. 14 gói.
Đáp án đúng là: C.
Vì giá bánh tăng lên 25% nên giá bánh mới sẽ bằng 125% giá bánh gốc.
Ta có 125% = , do đó giá bánh mới bằng giá bánh gốc.
Gọi số gói bánh mà bác Linh sẽ mua được là x (gói).
Vì số gói bánh mua được tỉ lệ nghịch với giá tiền một gói bánh nên tỉ số của số gói bánh mua dự định với số gói bánh mua thực tế là .
Do đó ta có: .
Vậy số gói bánh mà bác Linh mua được là: x = (gói).
Vậy bác Linh sẽ mua được 12 gói bánh.
Câu 26. Một thợ mộc 1 tuần làm được 15 sản phẩm. Hỏi để làm được 45 sản phẩm thì cần bao nhiêu ngày? Biết năng suất làm việc của người thợ đó không thay đổi.
A. 3 ngày;
B. 12 ngày;
C. 15 ngày;
D. 21 ngày.
Đáp án đúng là: D.
Đổi 1 tuần = 7 ngày.
Gọi x (sản phẩm) và y (h) lần lượt là số sản phẩm và thời gian làm ra số sản phẩm tương ứng của người thợ mộc đó (x, y > 0; x, y ).
Vì số sản phẩm và thời gian làm số sản phẩm đó tỉ lệ thuận với nhau nên theo tính chất tỉ lệ thuận ta có: .
Thay x1 = 15; y1 = 7; x2 = 45 ta có:
Suy ra
Vậy trong 21 ngày người thợ mộc đó sẽ làm được 45 sản phẩm.
Câu 27. Cứ đổi 1 158 000 đồng Việt Nam thì được 50 đô la Mỹ.
(Nguồn: https://portal.vietcombank.com.vn, cập nhật vào 18 giờ 30 phút ngày 07/5/2021)
Vậy nếu có 100 đô la Mỹ thì đổi được bao nhiêu tiền Việt Nam?
A. 230 000 đồng;
B. 2 316 000 đồng;
C. 579 000 đồng;
D. 5 790 000 đồng.
Đáp án đúng là: B.
Gọi x (đô la) và y (đồng) lần lượt là số tiền đô la Mỹ và số tiền Việt Nam đổi ra tương ứng.
Số tiền đô la Mỹ và số tiền Việt Nam tỉ lệ thuận với nhau nên theo tính chất tỉ lệ thuận ta có: .
Thay x1 = 50; y1 = 1 158 000; x2 = 100 ta được:
Suy ra (đồng)
Vậy nếu có 100 đô la Mỹ, ta đổi được 2 316 000 (đồng) Việt Nam.
Câu 28. Để thu được một loại đồng thau, người ta pha chế đồng và kẽm nguyên chất theo tỉ lệ 6 : 4. Tính khối lượng đồng nguyên chất cần thiết để sản xuất 5 kg đồng thau.
A. 0,5 kg;
B. 2 kg;
C. 3 kg;
D. 4 kg.
Đáp án đúng là: C.
Gọi x (kg) và y (kg) lần lượt là khối lượng đồng và kẽm cần thiết để sản xuất 10 kg đồng thau (x > 0, y > 0).
Theo đề bài ta có x + y = 10 và .
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Suy ra do đó x = 6.0,5 = 3;
Vậy khối lượng đồng nguyên chất cần thiết để sản xuất 5 kg đồng thau lần lượt là 3 kg.
Câu 29. Bạn Minh mua tổng cộng 34 quyển vở gồm ba loại: loại 120 trang giá 6 nghìn đồng một quyển, loại 200 trang giá 9 nghìn đồng một quyển và loại 240 trang giá 10 nghìn đồng một quyển. Hỏi Minh mua bao nhiêu quyển vở loại 240 trang, biết rằng số tiền bạn ấy dành để mua mỗi loại vở là như nhau?
A. 20 quyển;
B. 15 quyển;
C. 10 quyển;
D. 9 quyển.
Đáp án đúng là: D.
Gọi số vở Minh mua ba loại 120 trang, 200 trang và 240 trang lần lượt là x, y, z quyển (x, y, z > 0 và x, y, z ).
Bạn Minh mua tổng cộng 34 quyển vở nên ta có x + y + z = 34.
Do số tiền Minh dành để mua mỗi loại vở là như nhau nên 6x = 9y = 10z.
Do đó .
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
.
Suy ra: do đó hay z = 9;
Vậy Minh mua 9 quyển loại 240 trang.
Câu 30. Biết và 2x – 3y + z = 42. Giá trị của x, y, z là:
A. x = 20; y = 30; z = −92;
B. x = −20; y = 30; z = 92;
C. x = 20; y = 30; z = 92;
D. x = 20; y = −30; z = 92.
Đáp án đúng là: C.
Từ dãy tỉ số bằng nhau suy ra
Hay
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra:
+) do đó 2x + 2 = 7.6 = 42 suy ra 2x = 42 – 2 = 40 nên x = 40 : 2 = 20;
+) do đó 3y – 6 = 7.12 = 84 suy ra 3y = 84 + 6 = 90 nên y = 90 : 3 = 30;
+) do đó z – 1 = 7.13 = 91 suy ra z = 91 + 1 = 92.
Vậy x = 20; y = 30; z = 92.
Xem thêm các bài trắc nghiệm Toán 7 Cánh diều hay, chi tiết khác:
Trắc nghiệm Toán 7 Bài 8: Đại lượng tỉ lệ nghịch
Trắc nghiệm Toán 7 Bài 1: Hình hộp chữ nhật. Hình lập phương
Trắc nghiệm Toán 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác