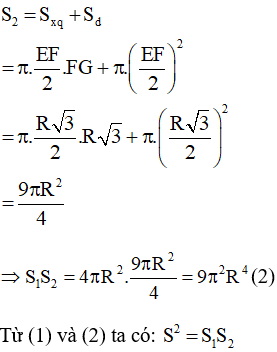Với giải Bài 44 trang 130 Toán lớp 9 chi tiết trong Ôn tập chương 4 Hình học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài Ôn tập chương 4 Hình học

Bài 44 trang 130 SGK Toán lớp 9 Tập 2: Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:

a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.

b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.

Lời giải:

a)

Khi hình vuông ABCD quay quanh trục GO ta được hình trụ có đường kính đáy AB và chiều cao BC là:

$V=\pi {\left(\frac{AB}{2}\right)}^2.BC$

Mà AB = BC (do ABCD là hình vuông)

$\Rightarrow V=\pi {\left(\frac{AB}{2}\right)}^2.AB$$=\pi \frac{A{B}^3}{4}$

Do ABCD là hình vuông nên ta có: $AC\perp BD$ tại O

Do đó, tam giác OAB vuông tại O

Xét tam giác OAB vuông tại O

Áp dụng định lý Py–ta–go ta có:

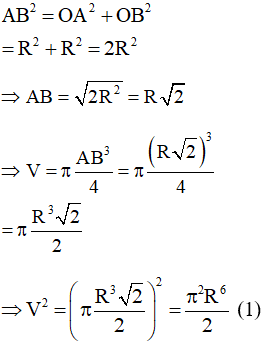
Thể tích hình cầu có bán kính R là:

$V_1=\frac{4}{3}\pi R^3$

Kẻ GH vuông góc với EF tại H

Thể tích hình nón có bán kính đường tròn đáy bằng $\frac{EF}{2}$ là: $V_2=\frac{1}{3}\pi {\left(\frac{EF}{2}\right)}^2.GH$

Do tam giác GEF đều nên

GH là đường cao (do GH vuông góc với EF tại H) và cũng là đường trung tuyến

$\Rightarrow HE=HF=\frac{EF}{2}$

Xét tam giác GEH vuông tại H

Áp dụng định lý Py–ta–go ta có:

$G{E}^2=G{H}^2+H{E}^2$

Mà GE = EF (do tam giác GEF đều)

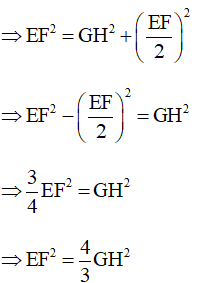
Do tam giác GEF đều nên O là trực tâm và cũng là trọng tâm

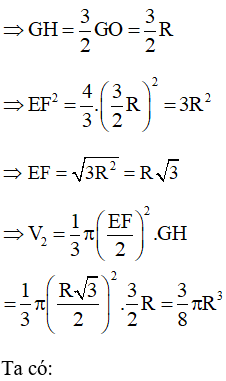
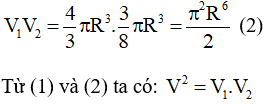
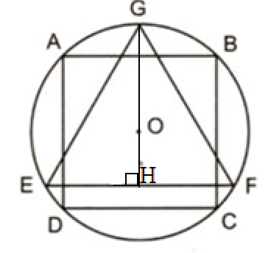
b)

Diện tích toàn phần của hình trụ có bán kính  $\frac{AB}{2}$ và chiều cao BC là:

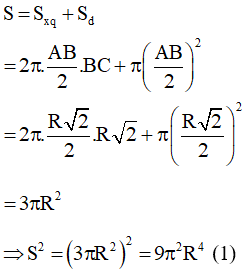
Diện tích mặt cầu có bán kính R là: $S_1=4\pi R^2$

Diện tích toàn phần của hình nón là: