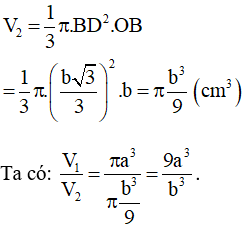Với giải Bài 41 trang 129 Toán lớp 9 chi tiết trong Ôn tập chương 4 Hình học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài Ôn tập chương 4 Hình học

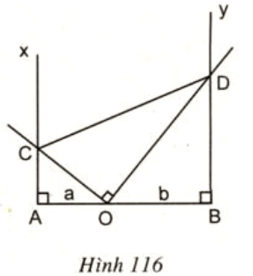
Bài 41 trang 129 SGK Toán lớp 9 Tập 2: Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a, OB = b (a, b cùng đơn vị: cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).

a) Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi.

b) Tính diện tích hình thang ABDC khi $\widehat{COA}={60}^o$.

c) Với $\widehat{COA}={60}^o$ cho hình vẽ quay xung quanh AB. Hãy tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành.

Lời giải:

a)

Tam giác BOD vuông tại B (do Bx vuông góc với AB tại B)

$\Rightarrow \widehat{BDO}+\widehat{BOD}={90}^o \left(1\right)$

Mặt khác, A, O, B thẳng hàng nên ta có:

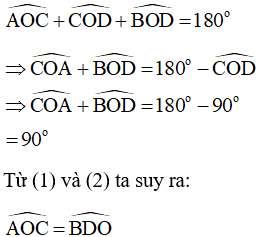
Xét hai tam giác vuông AOC và BDO ta có:

 $\widehat{A}=\widehat{B}={90}^o$

$\widehat{AOC}=\widehat{BDO}$ (chứng minh trên)

Do đó, tam giác vuông AOC và tam giác vuông BDO đồng dạng với nhau (góc – góc)

$\Rightarrow \frac{AC}{AO}=\frac{BO}{BD}\Rightarrow \frac{AC}{a}=\frac{b}{BD}$ (1)

Vậy AC.BD = a.b không đổi

b)

Khi $\widehat{COA}={60}^o$, xét tam giác vuông ACO có:

$$\begin{gathered} \tan \widehat{AOC}=\frac{AC}{OA} \\ \Rightarrow \tan {60}^o=\frac{AC}{a} \\ \Rightarrow AC=\tan {60}^o.a=a\sqrt{3} \end{gathered}$$

Mà: AC.BD = ab (câu a)

$$\begin{gathered} \Rightarrow a\sqrt{3}.BD=ab \\ \Rightarrow BD=\frac{b\sqrt{3}}{3} \end{gathered}$$

Diện tích hình thang ABCD có AC // BD (do cùng vuông góc với AB) là:

$$\begin{gathered} S=\frac{AC+BD}{2}.AB \\ =\frac{a\sqrt{3}+\frac{b\sqrt{3}}{3}}{2}.(a+b) \\ =\frac{\sqrt{3}}{6}(3a^2+4ab+b^2)\left(c{m}^2\right) \end{gathered}$$

c)

Theo đề bài ta có:

Tam giác AOC khi quay quanh cạnh AB tạo thành hình nón có chiều cao OA = a và bán kính đáy $AC=a\sqrt{3}$ nên thể tích hình nón là:

$$\begin{gathered} V_1=\frac{1}{3}\pi .A{C}^2.OA \\ =\frac{1}{3}\pi .{\left(a\sqrt{3}\right)}^2.a=\pi a^3\left(c{m}^3\right) \end{gathered}$$

Tam giác BOD khi quanh quanh cạnh AB tạo thành hình nón có chiều cao OB = b và bán kính đáy $BD=\frac{b\sqrt{3}}{3}$ nên thể tích hình nón là: