Với giải Vận dụng trang 52 Toán lớp 7 Chân trời sáng tạo chi tiết trong Chương 3 Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Chương 3 Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Vận dụng trang 52 Toán lớp 7: Để tính thể tích một hòn đá, bạn Na đã thực hiện như sau:

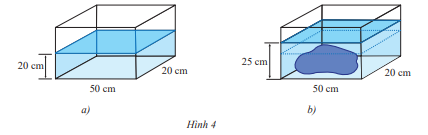
- Bạn ấy đổ nước vào cái bể kính hình hộp chữ nhật có hai đáy là 50 cm, 20 cm, mực nước đo được là 20 cm. (Hình 4a)

- Sau đó, bạn ấy đặt hòn đá vào bể thì thấy nước ngập hòn đá và mực nước đo được là 25 cm (Hình 4b)

Em hãy giúp bạn Na tính thể tích của hòn đá.

Phương pháp giải:

Thể tích của phần nước dâng lên chính là thể tích của hòn đá

Bước 1: Tính thể tích của phân nước trước khi thả đá và sau khi thả đá

Bước 2: Tính thể tích chênh lệch giữa 2 thời điểm

Thể tích của hình hộp chữ nhật có chiều dài, rộng, cao là a,b,c là: V = a.b.c

Lời giải:

Thể tích của hòn đá là: 50.20.25 – 50.20.20 = 5 000 (cm3) = 5 lít

Lý thuyết Một số bài toán thực tế

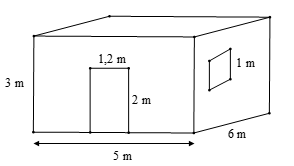
Ví dụ: Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một cửa sổ hình vuông với các kích thước như hình dưới. Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.

Hướng dẫn giải

Để tính được số tiền bác Long dùng để sơn căn phòng ta phải tính được diện tích phần cần sơn.

Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.

Diện tích xung quanh của căn phòng là:

S_xq = 2. (5 + 6) . 3 = 66 (m²).

Diện tích phần cửa lớn và cửa sổ là:

1,2 . 2 + 1 . 1 = 3,4 (m²)

Diện tích phần cần sơn là:

66 – 3,4 = 62,6 (m²).

Tổng chi phí cần để sơn là:

62,6. 30 000 = 1 878 000 (đồng).

Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.

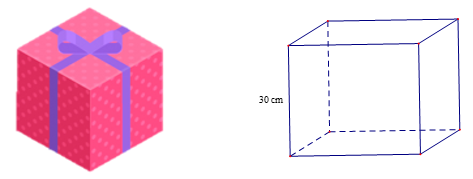
Ví dụ: Bạn Ngọc muốn làm một hộp quà hình lập phương có kích thước cạnh là 30 cm bằng tấm bìa. Em hãy tính diện tích phần tấm bìa cần dùng và thể tích của hộp quà.

Hướng dẫn giải

Hộp quà hình lập phương nên ta có:

Diện tích tấm bìa cần dùng sẽ bằng diện tích xung quanh của hình lập phương cộng với diện tích hai mặt đáy.

Diện tích xung quanh của hộp quà là:

S_xq = 4 . 30² = 3 600 (cm²).

Diện tích đáy của hình lập phương là:          

30 . 30 = 900 (cm²).

Vậy diện tích hai đáy của hình lập phương là:

2. 900 = 1 800 (cm²).

Diện tích tấm bìa cần dùng để làm hộp quà là:

3 600 + 1 800 = 5 400 (cm²).

Thể tích của hộp quà là 

V = 30³ = 27 000 (cm³).

Vậy diện tích tấm bìa cần dùng là 5 400 cm² và thể tích của hộp quà là 27 000 cm³.

Xem thêm các bài giải Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Thực hành trang 52 Toán lớp 7: Một khối bê tông, được đặt trên mặt đất có kích thước như hình 3...

Bài 1 trang 53 Toán lớp 7: Hùng làm một con xúc xắc hình lập phương có kích thước như Hình 5a từ tấm bìa có hình dạng như Hình 5b. Em hãy tính diện tích tấm bìa và thể tích con xúc xắc...

Bài 2 trang 53 Toán lớp 7: Hãy vẽ và gấp tấm bìa như Hình 6a thành một hình hộp chữ nhật như Hình 6b. Tính tổng diện tích các mặt và thể tích của hình hộp...

Bài 3 trang 53 Toán lớp 7: Một chiếc bánh kem dạng hình hộp chữ nhật với chiều dài 30 cm, chiểu rộng 20 cm và chiều cao 15 cm. Người ta cắt đi một miếng bánh có dạng hình lập phương cạnh 5 cm. Tính thể tích phần còn lại của chiếc bánh kem...

Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

Bài 1: Hình hộp chữ nhật – Hình lập phương

Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

Bài 5: Hoạt động thực hành và trải nghiệm: Các bài toán về đo đạc và gấp hình