Với giải Bài 63 trang 92 Toán lớp 9 chi tiết trong Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp
Bài 63 trang 92 SGK Toán lớp 9 Tập 2: Vẽ các hình lục giác đều, hình vuông, hình tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
Lời giải:
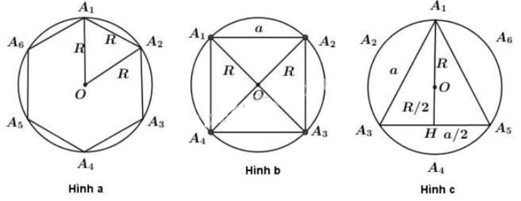
a) Hình a
Cách vẽ:
Vẽ đường tròn (O; R)
Trên đường tròn ta đặt liên tiếp các cung mà dây căng cung có độ dài bằng R.
Nối với , với , …. với ta được hình lục giác đều nội tiếp đường tròn
Tính cạnh:
Do là lục giác đều nên ta có:
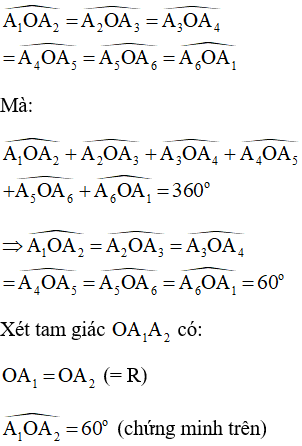
Do đó , tam giác là tam giác đều
Do đó, lục giác đều nội tiếp đường tròn (O; R) có cạnh là R.
b) Hình b
Cách vẽ:
- Vẽ đường kính của đường tròn (O; R)
- Vẽ đường kính
Tứ giác có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên là hình vuông
Nối với , với , với , với ta được hình vuông nội tiếp đường tròn (O; R)
Tính cạnh:
Xét hình vuông có:
Hai đường chéo tại O nên tam giác vuông tại O
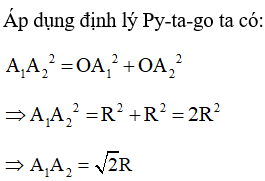
Vậy hình vuông nội tiếp đường tròn (O; R) có cạnh là .
c) Hình c
Cách vẽ:
Vẽ đường tròn (O; R)
Trên đường tròn ta đặt liên tiếp các cung mà dây căng cung có độ dài bằng R.
Nối với , với , với ta được hình tam giác đều nội tiếp (O; R)
Tính cạnh:
Kẻ đường cao của tam giác đều ta có:
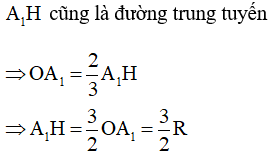
Mà H là trung điểm của (do cũng là đường trung tuyến)
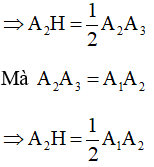
Xét tam giác vuông tại H (do là đường cao)
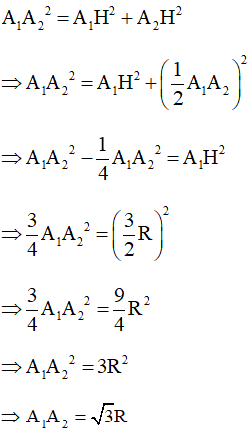
Vậy hình tam giác đều nội tiếp (O; R) có cạnh là .